利用排队论探讨计算机处理任务的效率问题

刘原笛

摘 要 当今时代科技迅速发展，计算机技术也越来越成熟。计算机在日常生活中被广泛应用于解决复杂的问题或任务，其效率便成为了人们关注的重点。文章针对这个问题，根据排队论原理，建立数学模型，对处理器数量与使用者的体验情况进行对比分析，并得出结论。

关键词 排队论；处理器数量；使用者体验

中图分类号 TP3 文献标识码 A 文章编号 1674-6708（2018）223-0130-02

近年来，计算机已被广泛应用于生活中的方方面面，并常被用来解决复杂计算问题。计算机虽然给我们带来了很大的便利，但也存在一些不足之处，例如在使用计算机时，经常会遇到计算机卡顿的现象，甚至出现死机的情况。因此，如何使计算机处理任务更加快速、有效，就是文章要探讨的课题。

1 排队论的概念

计算机使用者希望使用计算机进行复杂运算，如果有空闲的计算资源，使用者的任务便可以直接被处理，如果资源已被占用，其任务就会在一旁等待，并产生排队现象。文章通过运用排队论相关原理，并根据资料，结合具体情况，来解决计算机处理任务的效率问题。

排队论，或称随机服务系统理论，是数学统筹学的分支学科，也是研究服务系统中排队现象随机规律的一门学科。它通过统计研究服务对象到来及服务时间，得出这些数量指标（排队长度、等待时间、忙期长短等）的统计规律，然后来重新组织被服务的对象或改进服务系统的结构，使得服务系统的某些指标达到最优，又能同时满足服务对象的需要。它广泛应用于生产、库存、運输、计算机网络等各项资源共享的随机服务系统。

2 模型建立

2.1 模型分析

排队论是研究拥挤现象的一门数学学科，其核心研究内容是通过计算排队过程中各种任务的概率，来解决系统的最优设计和最优控制。从排队系统进程的主要因素看，它主要由3部分组成：输入过程、服务机构、排队规则。

2.2 模型假设

任务的到达情况有很多种，可能是一个一个来的，也可能是一次来好几个，现假设使用者提供的任务是打包的，每4个任务为一组，于是根据概率理论，假设任务的到来符合泊松分布。

假设每个复杂的任务都需要计算机消耗20分钟来解决。一个处理器可以同时解决4个问题。

排队规则：符合先到先服务的原则，假设所有任务只要计算机有空闲资源便立刻进行计算，计算机无空闲计算资源任务便自动进入队列等待，没有排队中途任务取消的现象。

模型：以三个处理器和四个处理器为例进行讨论。

服务机构属于多服务台并联，如图1所示。

2.3 符号说明

使用的符号：处理器数量（C），平均到达率（λ），单处理器服务率（μ），总服务率（Cμ），服务强度（ρ），空闲时间（P0），排队长（Lq），等待时间（Wq），队长（Ls），逗留时间（Ws）。

根据假设，并结合排队论模型，当ρ<1的稳态情况下有以下公式：

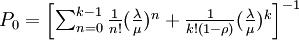
2.4 模型计算

模型1：假设有3个处理器，到达的任务按4个一组到来，且到来规律符合泊松分布。每个任务需要1/3小时的处理时间，处理规则为每次每个处理器同时有4个任务进行。按以上的稳态模型计算，单处理器服务率（μ）为3组/小时，故Cμ=9。经计算，队长（Lq）与等待时间（Wq）在平均到达率（λ）为8时会出现激增情况，队长（Ls）会由λ=8的9.0467激增至λ=8.8的45.0989。

模型2：假设有4个处理器，任务按一组4个到来，且到来的规律符合泊松分布，每个任务需要1/3小时处理，处理规则为每次每个处理器同时有4个任务进行。按以上稳态模型计算，单处理器服务率（μ）为3组/小时，故Cμ=12。经计算，在队长（Lq）与等待时间（Wq）在平均到达率（λ）为10时会出现激增情况，队长（Ls）会由λ=10的6.6219激增至λ=11的12.7058。

模型3：假设有4个处理器，现改变处理方式，在处理之前任务按组到来，且在处理之前先重新分组，每组2个，到来速度与上一种方案相同，到来规律符合泊松分布。其运动规则为：一处理器共两组4人，10分钟为一周期，处理满20分钟的组完成，并不断轮换。按以上稳态模型计算，单处理器服务率（μ）为6组/小时，故Cμ=24。因为模型改变，所以人员到来的效率相同时，平均到达率（λ）为原来的2倍。经计算，在人员到来速率相同的条件下，队长（Lq）的变化情况与模型2相同，仅等待时间缩短为原来的一半。

3 得出结论

1）将计算结果中的数值取整，并将小时化为分钟，通过模型1与2的对比整理之后可以得出折线图，如图2。

通过分析发现，三个处理器时在平均到达率为7时，出现队长（Lq）和等待时间（Wq）激增情况；在平均到达率为3以下时，两种方案的数据差距不大。

2）将数据中的数值取整，并将小时化为分钟之后，通过表2与表3的对比整理之后可以根据数据列得折线图，如图3。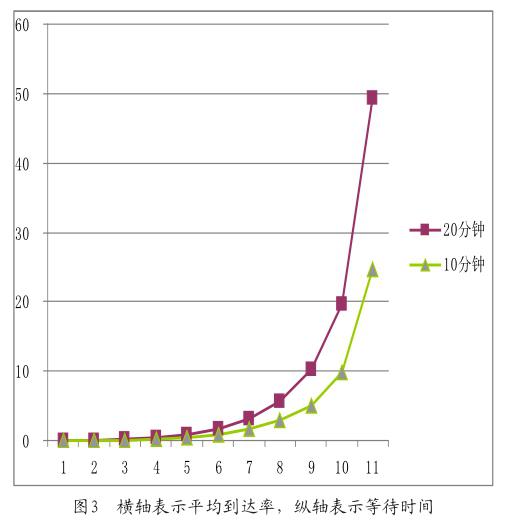

通过观察发现，新的方式相比较原来的方式，在条件与时间不变的情况下，可以让使用者的体验提升很多，故可以提倡这种规则，提高使用者的体验。

4 结论

根据本文的探讨，可以根据相应拓展计算，计算出更多的需求与处理器的关系，帮助管理者如何使计算机资源利用最大化。本次建模仅仅考虑了ρ<1的情况，对于另一种情况因为资料不足便没有讨论。期望今后随着计算机技术的不断发展，人们能够逐渐克服这一缺点，使其处理较多任务时能够更加高效化，为人们的工作和生活提供更大的便利。

参考文献

[1]陆传赉.排队论（第2版）[M].北京：北京邮电大学出版社，2009：2-7.

[2]张海君，郑伟.大话移动通信[M].北京：清华大学出版社，2011：35-36.

[3]豆丁网.http：//www.docin.com/touch/detail. do？id=487580791.

[4]豆丁网.http：//www.docin.com/p-1074674514.html.