基于有限测点的空调系统性能在线监测方法

2018-12-11

制冷学报 2018年6期

(1 上海交通大学制冷与低温工程研究所上海 200240； 2 海信科龙电器股份有限公司佛山 528303)

随着人们对房间空气舒适性能要求的日益提高，传统空调因控制方法陈旧、舒适度差、温度调节速度慢等原因已不能满足用户需求[1]，而智能空调通过对智能传感、互联网等技术的开发，使室内空气的智能调节成为可能[2-4]。智能空调的传感技术与互联网技术等应用的基础是对空调的运行数据进行采集与传输，而数据的采集是基于对制冷系统运行参数的实时监测[5-6]。

根据标准GB/T 7725—2004[7]，房间空调器制冷量和热泵制热量性能的测试方法主要为房间型量热计法[8]和空气焓值法[9-10]。但在用户实际使用过程中，没有条件采集风量、温湿度数据进行产品性能判定。只能通过测量制冷剂侧的参数，求出进、出口制冷剂的焓值和流量，计算系统制冷剂侧的换热量来获取系统的制冷量、制热量。

采用制冷剂侧的参数计算性能，需要获取制冷剂的质量流量。目前有研究通过测量载冷剂的流量进而计算出系统制冷量等参数，实现对中央空调系统性能的在线监测[11]，但该方法不适用于风冷式空调系统的监测。对于风冷式空调系统的监测，额外增加测量装置测量制冷剂流量会影响系统性能。

目前已有很多学者研究了半经验压缩机流量模型[12-14]，可以通过测量压缩机的吸、排气压力，结合实验数据计算得到制冷剂流量[15-16]。由于压力测点相较于温度测点成本较高，因此可以通过测量换热器铜管温度和进风温度，结合实验数据估算对应的饱和压力。

本文开发了基于有限测点的空调系统在线监测方法，包括空调系统的测点布置方法及根据测点的数据计算系统制冷剂质量流量、制冷量、压缩机功率的算法。

1 技术路线

空调系统的主要性能参数包括制冷量、制热量、整机功率、能效比等。

由于室内换热存在析湿现象，测量空气侧的热量变化对传感器的要求较高，而测量制冷剂侧的参数，计算制冷剂质量流量及室内机制冷剂进出口焓差，可以较为准确地得到换热量：

QR=mr(hr,out-hr,in)

(1)

式中：QR为室内机换热量，W；mr为制冷剂质量流量，kg/s；hr,out为室内机制冷剂出口焓值，kJ/kg；hr,in为室内机制冷剂入口焓值，kJ/kg。

综合考虑性能参数的计算精度和测量成本，对家用空调系统性能参数进行检测的思路为：在空调系统中布置温度、电流、电压测点，并建立测点数据和实验测得的温度、压力、质量流量、功率因数、室外侧电流等参数转化的模型，计算时依据模型逐步求解得到系统的性能参数。

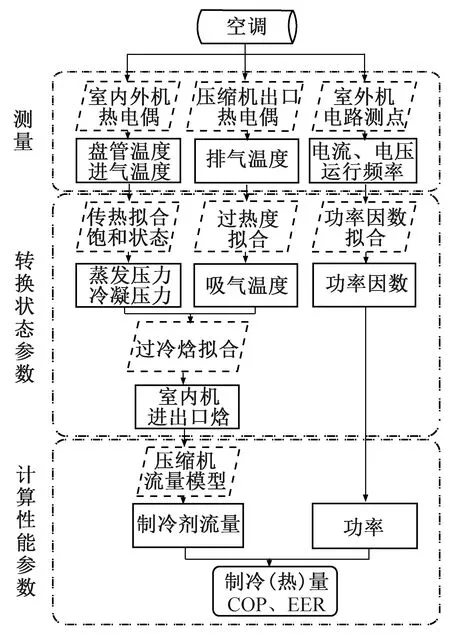
图1 系统性能在线监测技术路线Fig.1 Road map for air-conditioner performance monitoring

系统性能参数求解可分为两步：1)测点数据向压力、焓的转换：根据实验数据和物理特性对测点数据进行拟合，建立测点数据与系统中实际制冷循环参数的对应关系；2)质量流量、制冷量、功率等性能参数的计算：建立压缩机的质量流量模型，结合第一步得到的压力、焓、功率因数等数据计算空调系统的制冷量、制热量及能效比。本文认为蒸发压力和冷凝压力分别与吸、排气压力近似相等。

2 测点布置

图2所示为空调部件与对应测点示意图，系统部件由压缩机、室内机、膨胀阀、室外机组成，实际产品中共布置5个温度测点；另外，需要测量室外侧的电流、电压及压缩机的运行频率。

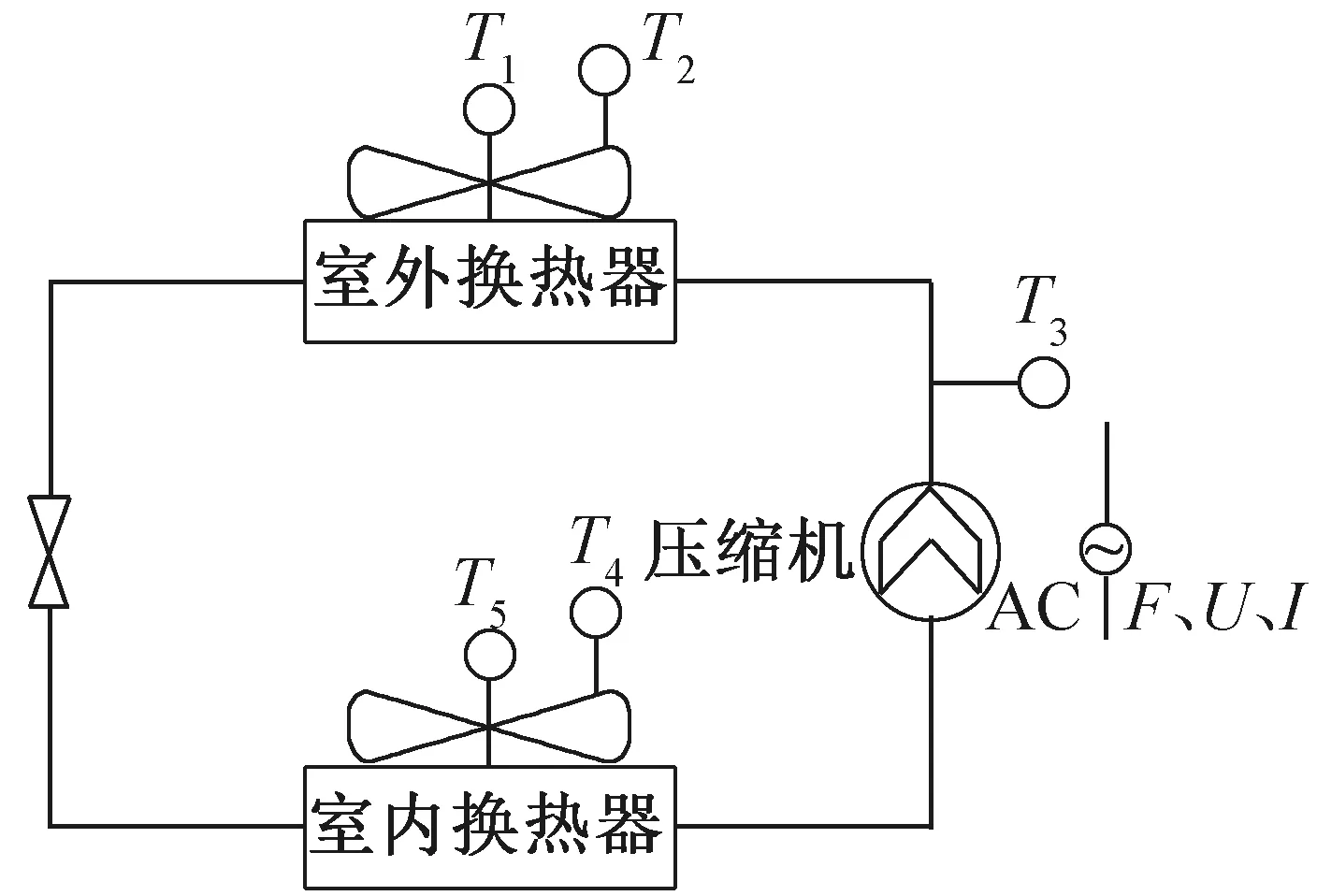
图2 空调部件与对应测点示意图Fig.2 Schematic diagram of air-conditiming components and corresponding measuring points

实际产品中测点的布置方案主要考虑以下因素：1) 测点能反应整个系统的运行情况，可用于求解制冷剂质量流量、室内机进出口焓差、功率等；2) 测点不影响空调系统的性能及可靠性，减少不必要的成本；3) 换热器温度测点布置在流路中部，使其能测得两相区的换热器铜管温度。

各个测点的测量精度如表1所示。

表1 测量精度Tab.1 Uncertainties of direct measurements

3 循环状态参数的转换

由于温度测点无法直接测量制冷剂的温度，需要对测点的温度值进行转换以得到相应的冷凝温度、蒸发温度等参数；测点的电流值为室外侧的总电流，由于变频空调中存在电感，需要进行转换才能得到整机的有效电流；而节流前后没有布置测点，需要根据实验数据及饱和点的焓值对该点的焓值进行估算。

3.1 电流的转换

测点的电流值为室外侧电流，加上室内侧的风机电流即为流入空调系统的总电流，可用线性公式表示测点电流与整机电流的关系。

由于变频器的存在，总电流不能直接用于计算，应结合功率因数转换为有效电流。当运行频率较高时，功率因数矫正装置(PFC)开启，功率因数PF(power factor)维持在0.9以上；当运行频率较低时，PFC关闭，功率因数较低。根据空调系统中PFC的开关状态，可分别用关于电流的二次多项式对PF进行拟合。总的有效电流可以拟合为以下形式：

(2)

式中：Iall为有效电流，A；I′为室外侧测点的电流，A；Ir为测点电流，A;PF为对应的功率因数。式中C1～C18均为拟合系数。

3.2 蒸发、冷凝压力的转换

冷凝压力和蒸发压力的转换精度直接影响质量流量的计算精度，制冷工况下的蒸发压力、制热工况下的冷凝压力还影响焓差的计算。出于成本考虑，本文通过测量进气温度与铜管表面温度拟合冷凝温度与蒸发温度，再根据制冷剂物性得出冷凝压力和蒸发压力。布置在换热器流路中部的温度测点，可反映两相段的壁温，通过拟合，可减少计算蒸发和冷凝温度的系统性偏差。如图3所示，测点为铜管外表面的温度，铜管与空气、管内制冷剂分别进行换热。

图3 换热器铜管温度测点示意图Fig.3 Coil temperature measurement points diagram

当温度稳定时，忽略铜内部的导热，温度可以表示为：

α1A1(T空气-T测点)+α2A2(T测点-T制冷剂)=0

(3)

即：

(4)

式中：α为表面传热系数，W/(m2·℃)；A为传热面积，m2。表面传热系数的计算较为复杂，这里可采用换热器铜管表面测点温度及进风测点温度来拟合制冷剂的冷凝温度，再计算得到该温度对应的饱和压力：

TC=C6TL+C7TA+C8

(5)

式中：TC为冷凝温度，℃；TL为对应的换热器铜管温度(制冷时为室外机液管温度T1，制热时为室内机液管温度T4)，℃；TA为对应的进风温度(制冷时为室外机进风温度T2，制热时为室内机进风温度T5)，℃。

实践表明，采用换热器铜管温度及进风温度对冷凝温度进行二维线性拟合，可以得到较好的拟合精度(相关系数R2>0.99)；但蒸发温度的拟合效果不理想，R2<0.8。考虑到蒸发压力与质量流量的变化关系很大，因此增加运行频率进行三维线性拟合，R2>0.99，拟合效果较好：

TE=C9TL+C10TA+C11F+C12

(6)

式中：TE为蒸发温度，℃；F为压缩机的运行频率，Hz；TL为对应的换热器铜管温度(制冷时为室内机液管温度T4，制热时为室外机液管温度T1)，℃；TA为对应的进风温度(制冷时为室内机进风温度T5，制热时为室内机进风温度T2)，℃。

3.3 吸气温度、节流焓的转换

系统中没有压缩机吸气状态和节流前后状态相应位置的测点，因此需要采用其他参数进行拟合。

压缩机的吸气温度用于计算压缩机的吸气密度及制冷工况下的室内机出口焓。由于没有吸气温度测点，本文采用排气过热度拟合吸气过热度，结合蒸发温度得到吸气温度。当排气过热度小于10 ℃时，吸气过热度通常小于2 ℃，而排气过热度较大时，吸气过热度才相应增加。本文采用排气过热度对吸气过热度进行二次拟合，R2>0.95，拟合结果如图4所示。

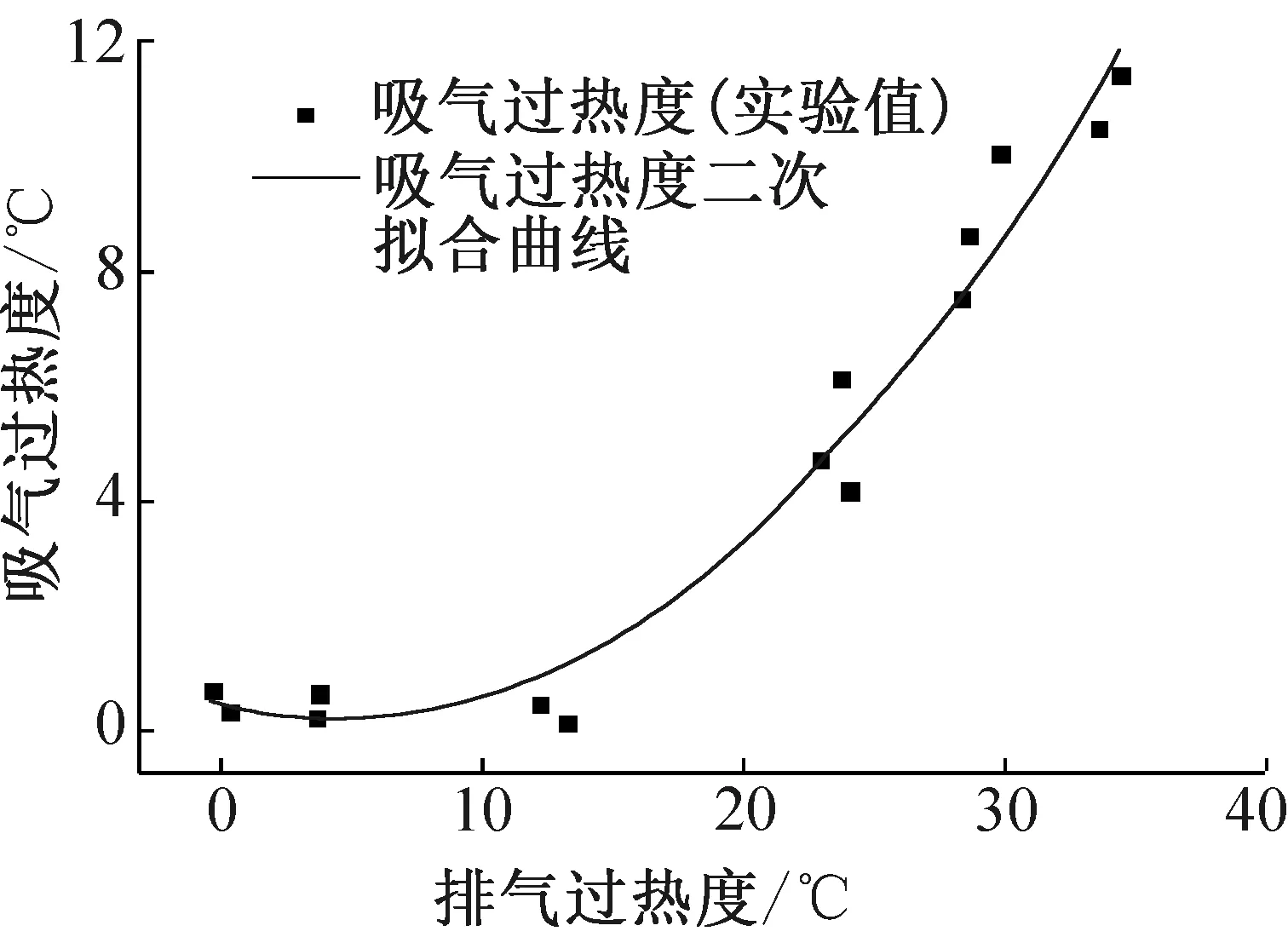
图4 吸气过热度拟合结果Fig.4 Fitting results of suction gas superheat

TS=C13(T3-TC)2+C14(T3-TC)2+C15+TE

(7)

制冷剂经过节流装置时的焓，在制冷工况下为室内机的进口焓，在制热工况下为室内机的出口焓。由空调系统的实际运行状态可知，节流前制冷剂应有一定的过冷度，节流后变为两相态，即节流前后的焓值应小于冷凝压力对应的汽化焓，应大于蒸发压力对应的汽化焓。结合实验数据，当运行频率较高时，过冷度较大；运行频率较低时，过冷度较小。

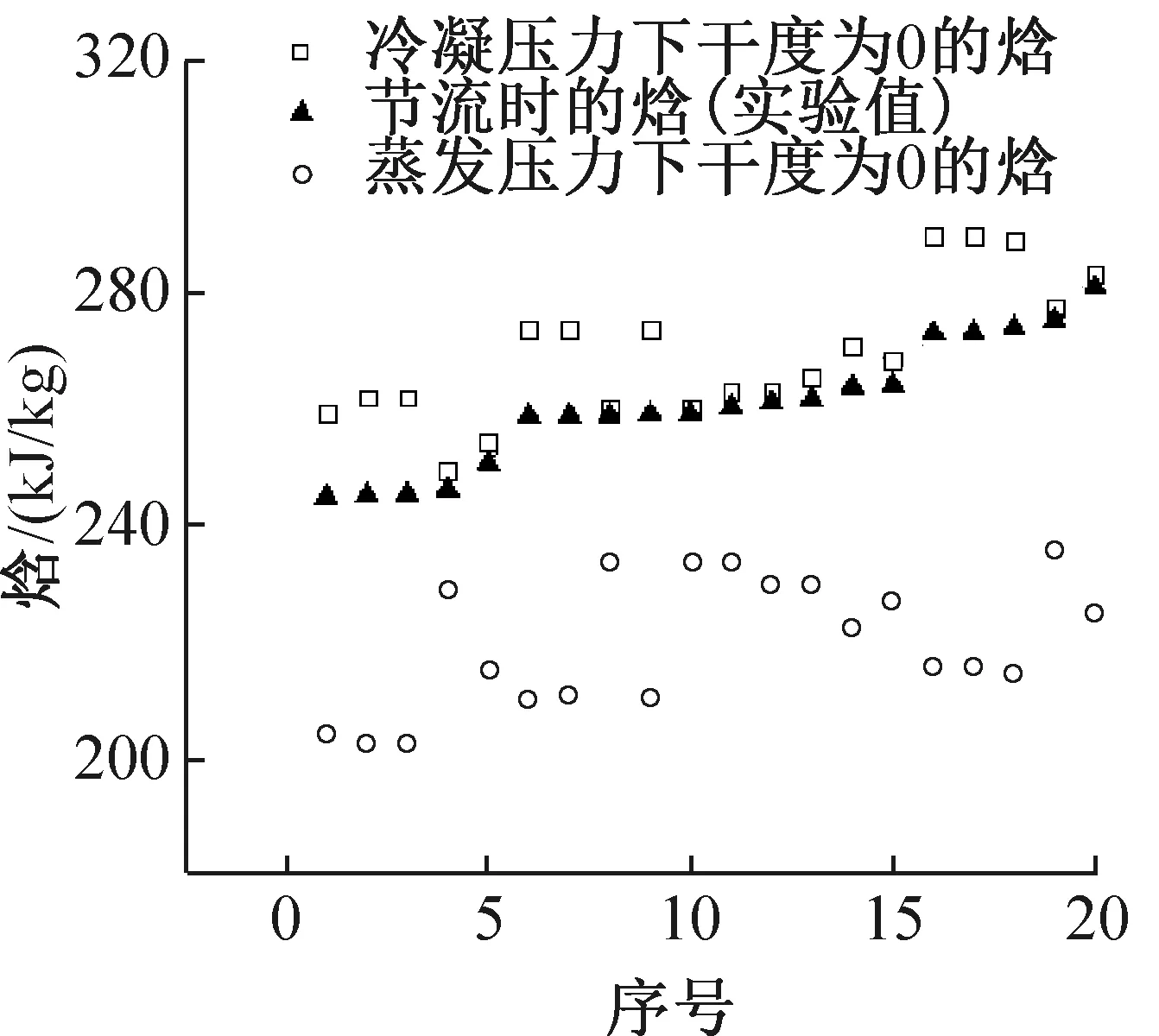
图5 节流焓示意图Fig.5 Refrigerant enthalpy diagram at the throttle

节流焓示意图如图5所示，节流时的过冷度与冷凝压力、蒸发压力有关，当冷凝压力较高时，过冷度较大；蒸发压力较低时(此时运行频率较高，质量流量较大)，过冷度较大。另外，随着风机的档位不同，略有变化。本文采用运行频率、蒸发压力下干度为0的焓、冷凝压力下干度为0的焓对过冷焓进行拟合：

hsc=C16hmin+C17hmax+C18F

(8)

式中：hmin为蒸发压力下干度为0的焓值，kJ/kg；hmax为冷凝压力下干度为0的焓值,kJ/kg。

4 流量模型与性能参数计算

4.1 在线监测压缩机流量模型

已有很多学者对半经验压缩机质量流量模型进行了研究，本文在前人研究的基础上，针对空调在线监测进行了改动。在线监测中，蒸发压力与冷凝压力不是直接测量得到，存在一定误差，因而对模型拟合实验数据的精度要求更高，以减少输入量变化对总误差的影响。

对于变频压缩机，当工作在特定频率时，其性能与工作在该频率下的定频压缩机相似，因此可将变频压缩机视为无数个工作在不同频率下的定频压缩机组成。对于定频压缩机，质量流量可用容积效率计算，而容积效率可由实验数据拟合得到。即：

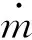
(9)

式中：λV为变频压缩机的输气系数；λV,ref为压缩机在定速下的参考输气系数；Vth为压缩机的理论容积输气量，m3/s；νsuc为开式压缩机环节吸气口的制冷剂气体比容，m3/kg；pC为冷凝压力，kPa；pE为蒸发压力，kPa。质量流量可由吸气温度、蒸发压力计算得到。根据容积效率比与定频部分质量流量的拟合形式中是否包含压力项一次、二次项和二次频率项，对以下6种流量拟合形式进行对比，得到相应拟合系数，并对比公式的拟合偏差，结果如表2所示。

f(F)f(pC,pE)=

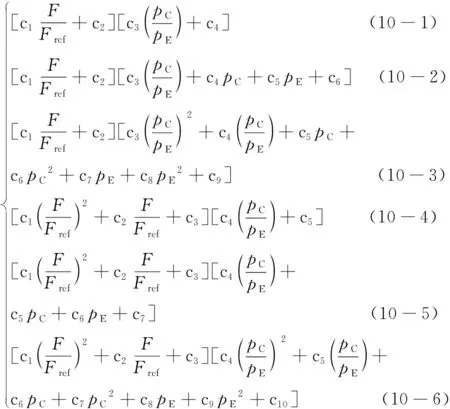
表 2 不同流量模型的拟合偏差对比Tab.2 Fitting errors for each mass flow rate equation

由表2可知，含拟合系数最多的式(10-6)平均偏差和最大偏差均最小，分别为1.4%和3.0%，拟合效果最好。

考虑到在线监测中，蒸发压力和冷凝压力一般存在一定偏差，需要质量流量模型在蒸发压力和冷凝压力略有变动时尽量保持稳定，表3对比了输入的蒸发压力和冷凝压力在100 kPa范围内变化时，式(10)对总流量的平均拟合偏差。

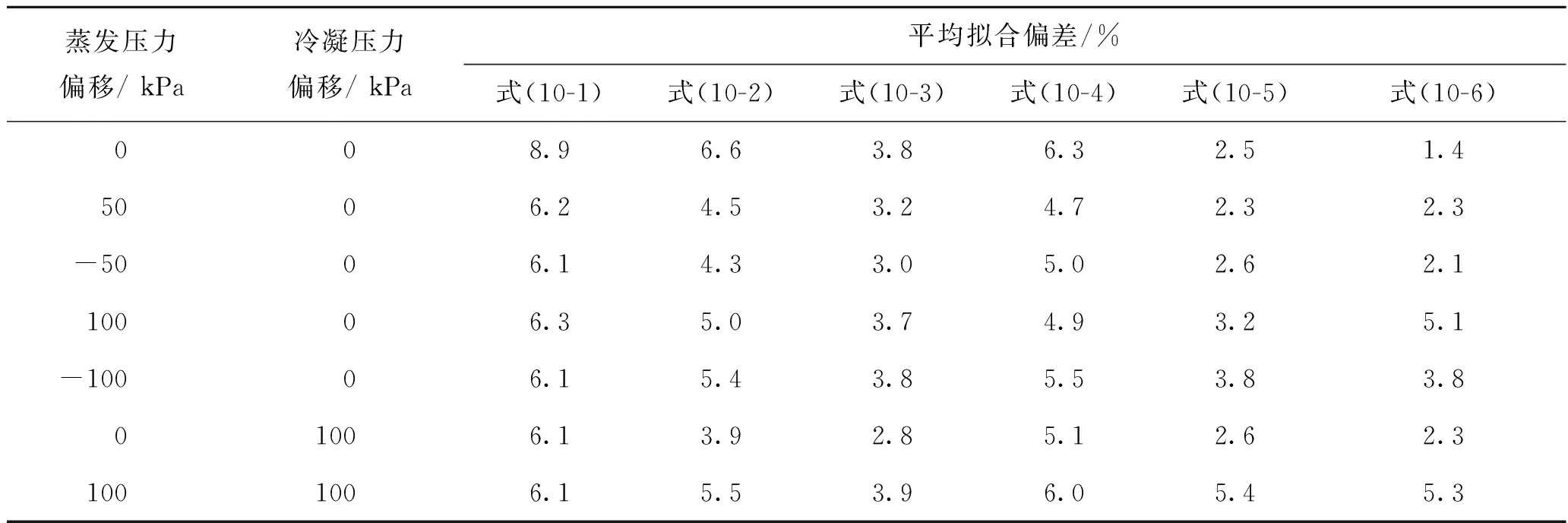
表 3 压力偏移时不同流量模型的平均拟合偏差对比Tab.3 Average fitting errors for each mass flow rate equation with pressure offsets

由表3可知，式(10-5)和式(10-6)蒸发压力在±50 kPa范围内变动时，流量计算结果变化较小；式(10-3)由于不含有频率的二次项，蒸发压力在±100 kPa范围内变动时，流量计算结果变化较小；冷凝压力的变化对流量的影响较小。

实际应用中，可根据蒸发压力与冷凝压力的转换精度，采用不同的拟合公式：当蒸发压力转换精度较高时，选用含有频率、压力一次、二次项的式(10-5)或式(10-6)；当蒸发压力及冷凝压力的转换精度较低时，选用不含频率二次项的式(10-3)。

4.2 室内换热量及能效的计算

依据测点数据转换得到的室内机进出口焓值及压缩机流量公式计算得到的质量流量，可由式(1)求得室内侧的换热量。功率可由测点数据转换得到的有效电流及电压计算得到。实验中发现测点的电压与外接电压计测得的电压存在0～6 V的压降，计算时可以加上一定的压降修正提高功率的计算准确性。

5 实验验证及误差分析

5.1 实验验证

根据海信科龙空调公司提供的空调在16个制冷工况及11个制热工况下的测点数据，按本文的性能参数算法，得到的性能参数与实验数据的偏差如图6和图7所示。

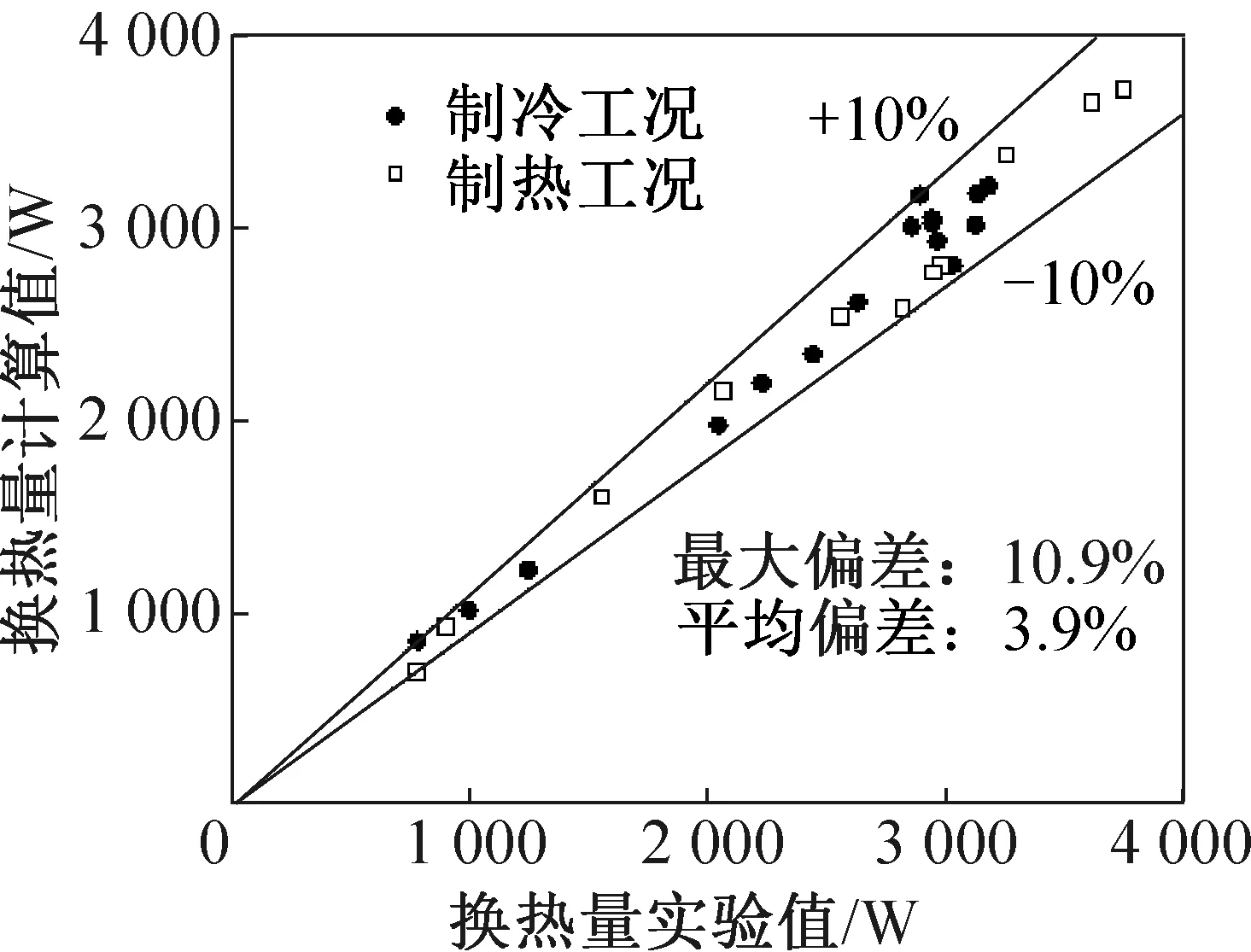
图6 换热量计算值与实验值对比Fig.6 Comparison between calculation and experiment results of indoor unit heat exchange

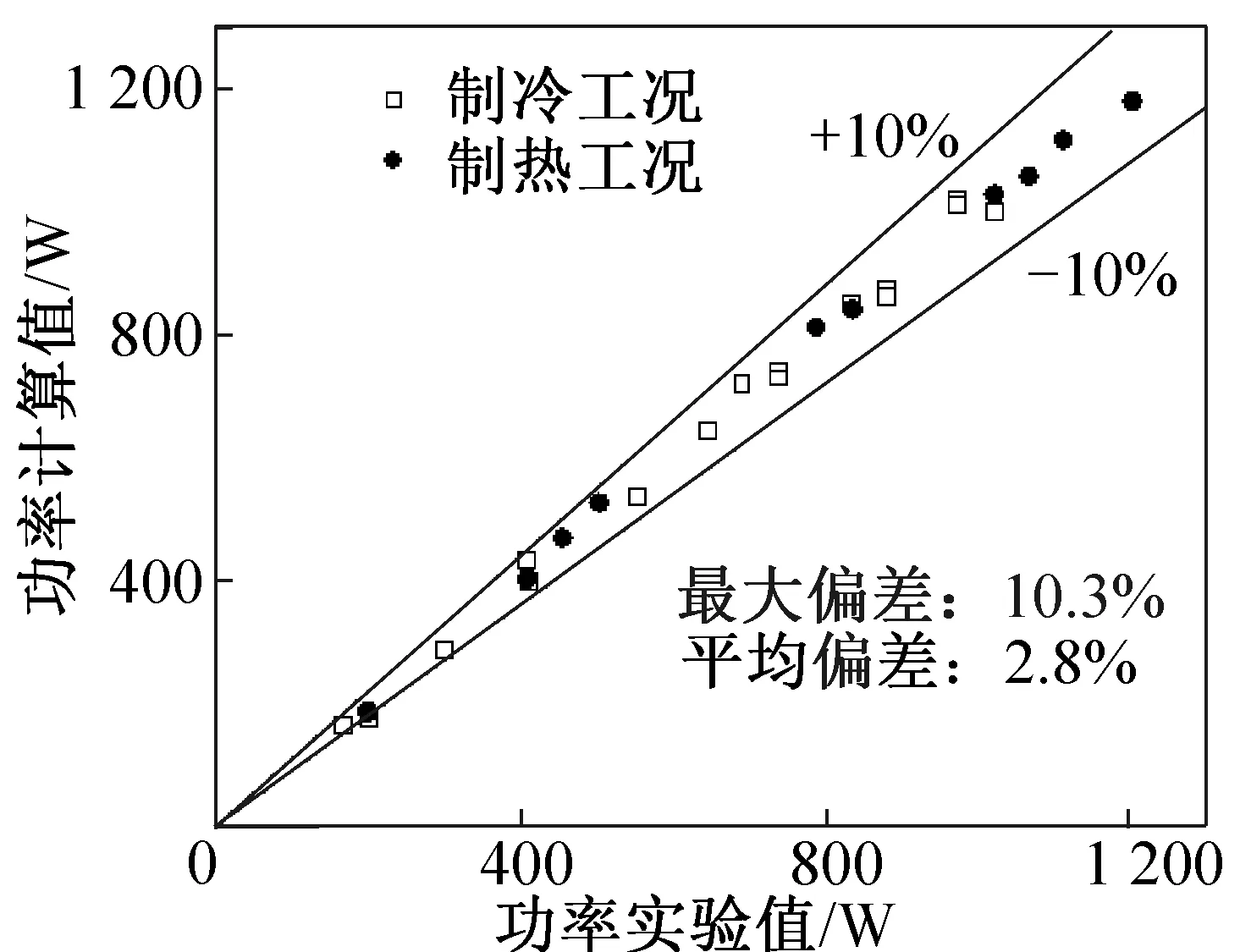
图7 功率计算值与实验值对比Fig.7 Comparison between calculation and experiment results of power consumption

由图6和图7可知，本文开发的各个系统性能参数的算法与实验实测值的最大偏差小于15%，满足在线监测的精度要求。

5.2 误差分析

为降低成本，空调系统中的温度测点的精度有限(±1 ℃)，在转换压力、焓等参数时也存在一定偏差。根据企业提供的实验数据，各中间变量与测量值的偏差如表4所示。

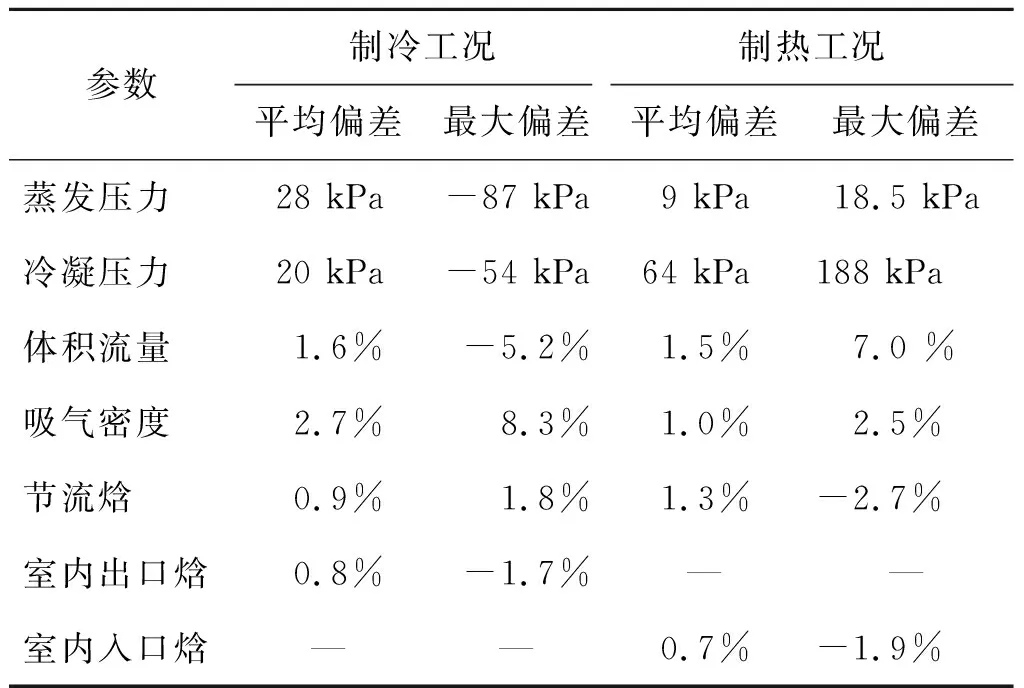
表4 循环状态参数的计算偏差Tab.4 Deviations of the calculated refrigerant state parameters

注：由于蒸发、冷凝压力计算偏差与制冷量不存在直接的对应关系，因此采用差值表示。

由表4可知，换热量的误差主要来源于质量流量计算，而流量的误差主要有两方面：1)温度测点的误差，产生蒸发、冷凝压力的计算误差，从而在计算体积流量时产生较大误差；2)蒸发压力误差与拟合吸气过热度的误差，导致计算吸气密度时产生误差。因此蒸发压力是本文换热量监测方法的主要误差来源，蒸发压力对体积流量、吸气密度和制冷工况下的室内机出口焓均有影响。增加蒸发压力测点可以有效提高换热量预测精度，但同时也会显著增加在线监测的成本。

功率的计算误差主要来自电流测量的误差与功率因数的拟合误差，改善电流测量的精度，可有效减少这部分误差。