非均匀温度分布对热电制冷芯片热端性能的影响

2018-12-11

制冷学报 2018年6期

(1 华中科技大学能源与动力工程学院武汉 430074； 2 张家港科瑞电器有限公司苏州 215624)

热电制冷技术通过帕尔帖效应直接将电能转化为热量或冷量，不依靠转动部件，无噪音，无污染，能够解决小体积电子设备的冷却问题[1-3]。但热电制冷系统的能量耗散比传统压缩式制冷系统大，性能系数也比传统压缩式制冷系统低很多[4-5]。

目前，提升热电制冷的性能主要有两种途径[6-7]：1)芯片优化，即TEC芯片的结构优化或材料优值系数优化[8-12]；2)通过热设计优化，即冷热端散热优化，降低热阻并提升性能系数[13-14]。关于降低冷热端温差以提高TEC芯片性能系数的研究较多，B. J. Huang等[15]指出热电制冷系统的设计需要通过迭代确定冷热端温差ΔT，而冷热端温差受热交换器的影响。胡韩莹等[16-17]研究了散热系统对热电制冷系统性能系数COP的影响，并指出采用基于相变的热管散热器可以大大降低热端热阻，提高系统COP。

TEC芯片工作性能依赖于热与电的强耦合作用，焦耳热及热端向冷端进行的热传导是导致热电制冷性能系数低的主要因素。因此，若TEC芯片具有非均匀的温度分布，则会使芯片上不同区域的传热量不同，且物性随温度的变化也会导致各个效应的变化。在温差发电领域，已有很多学者针对非均匀温度场对TEC芯片工作性能的影响进行了定性和定量研究[18-20]，但在热电制冷领域还鲜有相关的定量研究。许生龙等[21]研究了TEC芯片温差不均匀程度对电偶工作性能的影响，证实了“横向热流”的存在。潘海俊等[22]研究了TEC芯片的非均温特性对内部焦耳热的影响并给出了温度和热流量的分布公式。朱仁江等[23]使用有限元方法对一种点热源散热进行了非均匀热流分析，但只进行了定性分析，没有定量分析。因此，笔者认为有必要对TEC芯片的非均匀温度分布的影响进行定量研究。

本文针对一种热端理想非均匀温度场作用下的TEC芯片进行稳态分析，使用有限元分析方法进行模拟，探讨非均温特性对TEC芯片工作性能的影响，为TEC芯片的工程应用提供指导。

1 理论模型

1.1 控制方程

本文采用ANSYS workbench中提供的热电分析模块对TEC芯片温度分布和工作性能进行三维数值研究。

在热电问题分析中，热流控制方程和电势控制方程如下：

(1)

(2)

(3)

表 1 Bi2Te3的相关物性随温度的变化关系[24] Tab.1 The related physical parameters of Bi2Te3 vary with temperature

注：T的单位为K。

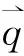
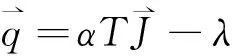
(4)

(5)

式中：α为塞贝克系数，V/K;λ为导热系数，W/(m·K)；σ为电导率，S/m。将式(4)和式(5)代入式(1)和式(2)可得：

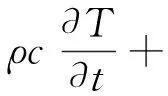
(6)

(7)

1.2 非均匀温度场边界条件

本文进行有限元分析的边界条件定义如下：假设在TEC芯片热端有一个因散热不良导致的圆形高温区域，该区域的大小可由面积常数ω来表示：

(8)

式中：d为假想高温区域的圆形直径，mm；L为正方形TEC芯片的边长，mm;ω为高温区面积常数，ω的变化可以代表高温区域的面积变化。

热端工作温度Th(℃)的分布为：

(9)

式中：tp为高温区中心点温度峰值，℃；th为无高温区域时热端的工作温度，℃。(tp-th)为高温区域最高温度超出工作温度的幅值，令θm为最高过余温度,℃：

θm=tp-th

(10)

非均匀温度场建立效果如图 1和图 2所示。图 1所示为二维温度分布，图 2所示为在三维空间上的温度分布。

2 计算方法

2.1 物性参数

本文以Bi2Te3作为分析材料进行模拟分析，其物性变化如表 1所示。其他材料的物性参数如表2所示，有限元分析的参数设置如表3所示。

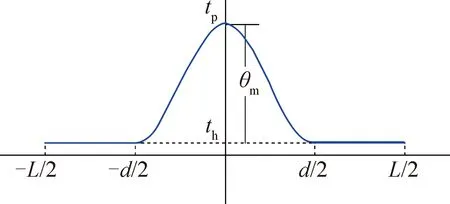
图1 非均匀温度场的二维分布Fig.1 2D temperature distribution

参数数值铜片导热系数λCu/(W/(m·K))400铜片的电导率σCu/(S/m)5.998×10-7陶瓷基板的热导率λcp/(W/(m·K))18

表3 有限元分析的参数设置Tab.3 Parameter setting for finite element analysis

图2 非均匀温度场的三维分布Fig.2 3D temperature distribution

2.2 有限元模型

有限元分析使用ANSYS workbench平台，选用Thermal-electric模块。为了分析非均匀温度场对TEC芯片性能的影响，考虑了128对热电偶的TEC芯片，计算模型如图 3所示。

图3 TEC芯片的分析模型Fig.3 Analysis model of TEC chips

为确保计算的有效性，对该模型进行网格独立性验证。在网格数分别为8 354、15 290、21 358、24 066时，对应TEC芯片冷端的制冷量分别为13.338 W、13.249 W、13.203 W、13.198 W。根据验证结果，当网格数≥21 358时，计算的制冷量基本不再受网格数变化的影响，网格数为24 066时计算的制冷量与网格数为21 358时只相差0.005 W，差距小于0.05%。为保证分析的可靠性并提升计算速度，本文选取网格数为21 358进行有限元分析。模拟分析时所采用几何参数如图 3所示。工况参数的设置如表3所示。

3 结果与讨论

3.1 温度场对制冷量的影响

本文计算中电流I=2.9 A。为对比非均匀温度场各项参数th、θm、ω的变化对制冷量Qc的影响，定义：

制冷量偏差：

ΔQc=Qc-Qcth

(11)

相对制冷量偏差：

(12)

式中：Qc与Qcth分别为相同th对应的非均匀和均匀温度分布下所得制冷量，W。

图4 非均匀温度场对TEC芯片ΔQc和ηΔQc的影响Fig.4 Influence of non-uniform temperature distribution on ΔQc and ηΔQc of TEC chips

图4所示为非均匀温度场对TEC芯片ΔQc和ηΔQc的影响。由图4可知，ΔQc和ηΔQc均为负数，说明非均匀温度场导致TEC芯片制冷量降低。从定量来看，过余温度θm对制冷量偏差影响最大，如图4(a)所示，|ΔQc|与|ηΔQc|随θm的变化接近线性关系；面积常数ω对制冷量偏差影响较大，由图 4 (b)可知，|ΔQc|与|ΔQc|均随着ω的增大而增大。热端工作温度th的变化对θm-ΔQc曲线和ω-ΔQc曲线几乎没有影响。说明相对于非均匀温度场的θm和ω，热端工作均温th对TEC芯片制冷量的影响较小，但由于th越高，制冷系统的制冷量越小[1]，所以th的增加使θm-ηQc曲线和ω-ηQc曲线升高，即非均匀温度场影响的|ηΔQc|增加。

3.2 温度场对功率的影响

温度场对TEC芯片功率的影响可通过每个电偶臂电势差与电流的乘积计算获得，即：

P=∑Pi=∑UiI

(13)

取总的电势差ΔU=∑Ui进行计算：

P=ΔUI

(14)

图5 TEC芯片的电压分布(ω=0.5，th=20 ℃，θm=20 ℃)Fig.5 The voltage distribution of the TEC chips

图 5所示为TEC芯片的电压分布，图5(a)为整个TEC芯片的电压分布，对每个电偶臂进行编号。芯片内热电偶串联连接，且不考虑各部分的接触电阻，因此可以看到TEC芯片的电压沿导体连续变化。图5(b)为对每个电偶臂两端的电压差进行统计后所得电压差分布。在非均匀温度场的均温部分，由于两种材料的电导率不同，n型半导体和p型半导体电偶臂的压降不同，但同一种材料电偶臂的压降相同。而在TEC芯片非均匀温度场的高温部分，电偶臂的压降明显高于其他部分，这是因为两种材料的电导率随着温度变化而变化。由表 1可知两种材料的电导率与温度成二次函数关系，且极小值均约为500 K，因此两种材料在20 ℃时的电导率高于40 ℃时，导致高温区的电偶臂的电导率小，压降更大。

为对比在电流不变时，非均匀温度场各项参数th、θm、ω变化对功率P的影响，定义：

功率偏差:

ΔP=P-Pth

(15)

相对功率偏差：

(16)

式中：P与Pth分别为相同th对应的非均匀和均匀温度分布下所得功率。

图 6所示为非均匀温度场对TEC芯片ΔP和ηΔP的影响。由图6可知，ΔP和ηΔP均为正数，说明该非均匀温度场导致TEC芯片的总功率增加。从定量来看，θm对功率偏差的影响最大。由图 6(a)可知，ΔP和ηΔP随θm的变化接近线性关系；由图 6(b)可知，ω对功率偏差的影响较大，ΔP和ηΔP均随ω的增大而增大。th对ΔP的影响最小，th的增大使ω-ηΔP曲线和θm-ηΔP曲线略有下降。说明相对于非均匀温度场的特性参数θm和ω，th对TEC芯片系统总功率的影响较小。由于th增大，制冷系统的功率略有增加，所以非均匀温度场影响的ηΔP降低。在图 6所示的工况中，当ω=0.75，th=20 ℃，θm=30 ℃时，TEC芯片的ΔP=0.870 W，ηΔP=2.608%。