巧用平面几何性质，解决与圆有关的问题

江苏省梁丰高级中学数学组 王 燕

直线和圆的位置关系在高考要求中属于“理解”，它是平面解析几何的基础。平面解析几何中解决这类问题的方法通常是坐标法，也就是将几何问题代数化、用代数的方法解决几何问题。考试大纲中对椭圆、双曲线、抛物线要求的弱化，更加凸显了直线与圆的地位，但是有些直线与圆的题目如果用代数法解决计算比较复杂，得分也就比较低。 圆的垂径定理和苏教版选修4-1《几何证明选讲》中割线定理、切割线定理、相交弦定理在考试大纲要求中属于“理解”。如果我们能够熟练应用圆的这几个定理，则一定会为我们解决解析几何中直线与圆的有关问题提供更为广阔的思维空间。

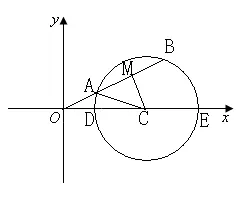
方法二：取弦AB的中点M，由垂径定理，设OA=x，AB=2x，两次利用勾股定理，得

评注：本题如果设直线方程后和圆方程联立来求弦长，AB=2OA这个条件用起来比较困难，而且计算比较复杂。这里巧妙利用圆的相交弦定理或垂径定理，使问题得到了顺利解决。

评注：本题若设两条直线的方程并与圆方程联立来解决，计算非常复杂，而且还需要讨论直线斜率是否存在，在此巧妙运用圆的垂径定理和基本不等式处理，使问题很快就迎刃而解。

例3 （2008年江苏省百所高中样本分析考试第18题）如图，已知圆A的半径是2，圆外一定点N与圆A上的点的最短距离为6，过动点P作A的切线PM（M为切点），连接PN，使得

（1）试建立适当的坐标系，求动点P的轨迹E；

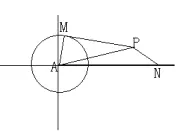
（2）方法一：设圆心（16,0），作圆的切线AK，连接MK。

方法二：设x轴与圆交于点Q，R，则由圆的割线定理得：

评注：本题第二问利用圆的切割线定理或割线定理，巧妙简化了计算，为求解其他题目可以赢得更多的时间。

例4 （2009届苏州五市三区高三数学九月调研测试卷第17题）已知圆，直线。

（1）求证：对m∈R，直线l与圆C总有两个不同的交点A、B；

（2）求弦AB的中点M的轨迹方程，并说明其轨迹是什么曲线；

（2）由垂径定理，CM⊥l, ∠CMP=90°，所以点M的轨迹是以CP为直径的圆，即以为圆心，为半径的圆（除掉点P（1,1））。所以AB的中点M的轨迹方程是：（除掉点P（1,1））。

（3）P（1,1）在直线l上，∴P，A，B共线。

过点P作圆C的直径EF，

评注：本题第（2）小题若将直线与圆联立得交点，再求中点，然后消去参数m，得中点的轨迹方程。大多数同学在求出后，不知如何消去参数m，也就无法得出轨迹了。这里我们利用圆的垂径定理，得中点M的轨迹是以CP为直径的圆（除掉点P（1,1））），巧妙地得到了解答，而且也简化了计算。

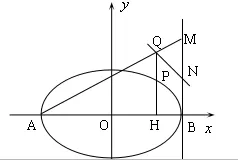
（1）求椭圆C的方程；

（2）证明点Q在以AB为直径的圆O上；

（3）试判断直线QN与圆O的位置关系。

（3）QN与圆O相切。

证明：连接OQ,ON,QB。

由（2）得，OQ=OB，∠AQB=90°，N为MB中点，所以QN=NB，OQ=OB，得出△OQN≌△OBN,所以∠OQN=∠OBN=90°，OQ⊥QN，QN与圆O相切。

评注：本题第三问研究直线与圆相切，可以利用斜率之积为-1，但是需要讨论分母是否为0，计算相对麻烦。在这里利用两个直角三角形全等，独辟蹊径，使问题得到圆满解决。

处理直线与圆的位置关系这一类的问题，如果我们能够换一种思路，从我们学习过的圆的性质入手，也许我们就能够找到柳暗花明又一村的感觉。如果我们平时能够积累一些处理类似问题的方法，在解决问题的时候也会往这方面想一想，而不是一味蛮干，这样也就达到了知识之间的融会贯通和综合运用的目的。