数形结合与有效课堂教学

江苏省苏州市吴中区木渎金山高级中学 顾维维

一、培养数形结合意识，寻找契合点

“冰冻三尺非一日之寒”，要让学生能够熟练掌握数形结合的思想方法，首先应培养学生具备数形结合的意识，这要求我们教师必须在平时的教学中经常渗透数形结合的思想方法，要注意培养学生这种思想意识，争取做到见数思形，见形想数。

分析：由于本题所给函数解析式结构较为复杂，没用明显突破点，运用常规办法难度较大，而且过程烦琐。仔细观察，可以发现题目所求可以看成是两段距离差值的最大值，将“数” 化成“形”来解决，值得一试。

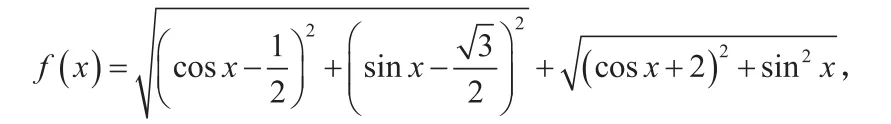
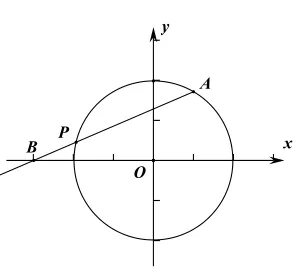
如图所示，结合图形可知，当A，B，P三点共线时，f（x）最小，此时

分析：题目已知的是分别关于a，b和c，d的两个方程，很一般，但是所求的形式却给了我们很好的灵感，它不就是两点间距离的平方吗？而这两点分别在所给方程对应的函数曲线上，那么强烈的数形结合意识便油然而生。

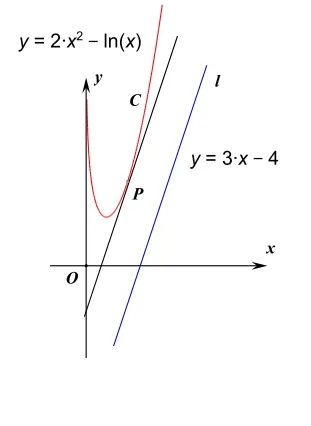
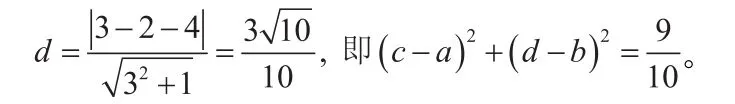
通过这两个例题可以看出，在平时教学中主动设置类似问题，引导学生仔细审题，认真观察，找到数形结合的契合点或者突破点，逐步培养数形结合的意识，由于数形结合是直观想象（数学核心素养要素之一）的重要内容，所以数形结合思想的渗透过程也是对学生数学核心素养的培养过程。

二、抓住本质，真正做到“心中有形”

（1）若f（x）≥0，求a的值；

分析：（1）问的解法很多，比如对a与0比较，进行分类讨论，或者参变分离，求导，求最小值等等。事实上，本题还可以通过数形结合来研究，当然，这种方法不一定最简单，笔者单纯从研究角度考虑本题的第（1）问。

解：令f（x）≥0，即x-1≥alnx，若a＜0，不妨取则显然不合题意。a=0时，取则 f（x）＜0，同样不合题意，故a＞0。

由于x-1≥alnx，该不等式所表示的含义可以这样理解：定直线y=x-1恒在过定点（1,0）的曲线y=alnx的上方，当a=1时，y=alnx在（1,0）处的切线是y=x-1，如下图中曲线C1所示，符合题意；

当a＞1时，如曲线C2，不符合题意；

当0＜a＜1时，如曲线C3，不符合题意。

所以，要满足定直线y=x-1恒在曲线y=alnx的上方，当且仅当a=1。

思维发散：事实上，本题还可以换个角度去研究，根据前面的分析可知a＞0，则x-1≥alnx可变形为那么问题转化为动直线恒在定曲线的上方，

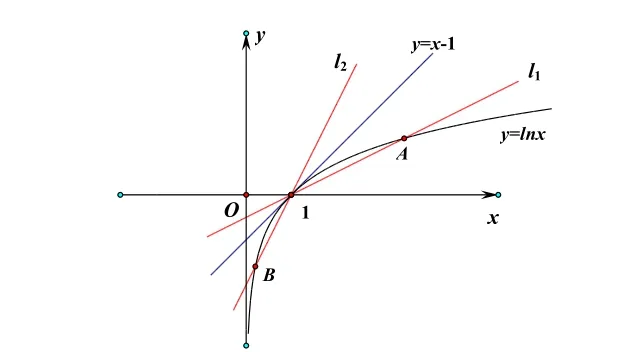
当a=1时，y=alnx在（1,0）处的切线是y=x-1，结合下图，符合题意；

当a＞1时，此时直线如下图l1所示，与y=lnx交于另一点A，不符合题意；

当0＜a＜1时，此时直线如下图l2所示，与y=lnx交于另一点B，不符合题意；

综上可知，a=1。

评注：本题以高考题为研究背景，运用数形结合，从多角度来展开探讨，在课堂上做开放性研究，教师适当引导，目的是要让学生知道如何去除问题表面，抓住数形结合的本质，同时又感受到数形结合的魅力，强化学生对数形结合的深刻理解，增强学生对数学的兴趣和轻松面对高考的信心。

在高中的教学中，我们经常会遇到许多相似的题目，这些题目大多数我们都很熟悉，作为教师，我们应该善于总结，发现内在联系和规律，形成知识体系，传授给学生，这样做能够开阔学生思维，增强学习兴趣和学习信心，同时可以有效避免题海战术以及学生一做就错，再做再错导致的消极学习心理。

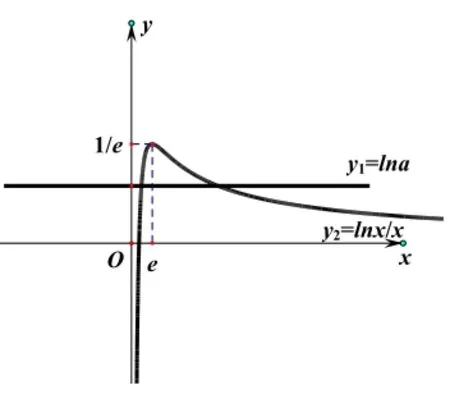
评注：两种解法首先均是利用y=ax(a＞1)的单调性得到以c，d为根的方程，解法1为常规解法，但解方程和不等式过程比较烦琐，而解法2比较灵活，首先对方程进行变形，转化为与常数函数y=lna的图像有两个交点问题，数形结合，答案一目了然。

当然，此时应趁热打铁，乘胜追击!

分析：本题若用一般方法解决，难度较大，若考虑数形结合，以函数的性质为依托，对函数进行适当变形，将原函数存在零点转为两条曲线有交点，那么问题便可迎刃而解。

图（1）

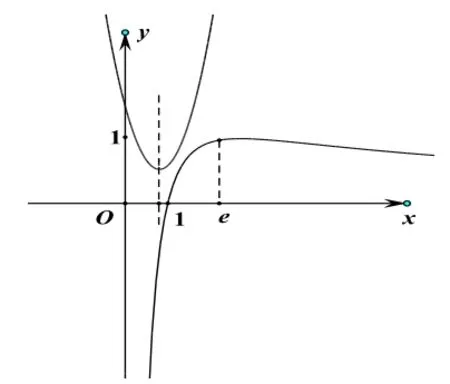
图（2）

数形结合的思想方法应始终贯穿在数学教学中，具体可以根据所授内容，结合学生实际情况，在我们的课堂教学和课后训练中不断渗透“数形结合”思想，事实上，这也是对学生数学核心素养的培养过程，在这个过程中，让学生感受到数学的魅力，增强其学习的兴趣和信心，快乐学习，同时也提高了学生的学习能力和解题能力。

在数学的学习和教学中，我们要仔细观察，善于总结，总结好的理论与思想，好的教学方法与对策，并实实在在地落实到每一节数学课堂中，切实提高教学实效。