浅谈“线性规划问题”常见题型及其求法

2018-12-10重庆市铁路中学校何成宝

中学生数理化(高中版.高二数学) 2018年11期

关键词：约束条件斜率整数

■重庆市铁路中学校何成宝

线性规划是运筹学的重要分支之一,也是高中数学教材中的重要内容之一,解题步骤是由已知条件写出约束条件,并作出可行域,进而通过平移直线在可行域内求线性目标函数的最优解。下面对线性规划常见的几类题型举例说明,希望对同学们的学习有所帮助。

一、已知线性约束条件,求线性目标函数的最值问题

例1若x、y满足约束条■件则z=x+2y的最小值是( )。

A.6 B.2 C.3 D.5

解：如图1,作出可行域。将直线l：x+2y=0向右上方平移,当过点A(2,0)时,有最小值2,故选B。

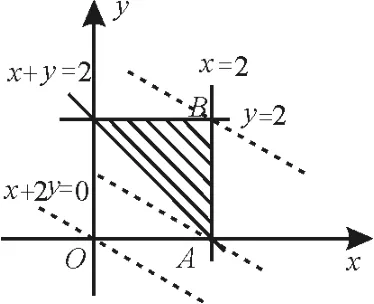
图1

点评：解决线性目标函数的最值问题,常将目标函数z=a x+b y转化为直线的斜截式：,通过求直线的截距的最值,间接求出z的最值。

变式训练1：设变量x、y满足约束条件的最大值为解：画出可行域,如图2所示。分析可得在直线2xy=2与直线x-y=-1的交点A(3,4)处,目标函数z取得最大值18。

图2

二、已知线性约束条件,求非线性目标函数的最值问题

例2已知x、y满足以下约束条件则z=x2+y2的最大值和最小值分别是( )。

A.13,1 B.13,2

解：如图3,作出可行域。x2+y2是可行域内的点(x,y)到原点的距离的平方,故最大值为点A(2,3)到原点的距离的平方,即|A O|2=13;最小值为原点到直线2x+y-2=0的距离的平方,解得值为。故选C。

图3

点评：解决非线性目标函数的最值问题,关键是先准确确定目标函数的几何意义,如表示点(x,y)与定点(a,b)的距离,表示点(x,y)与定点(a,b)连线的斜率,然后根据图形求最值。

变式训练2：已知则的取值范围是( )。

C.(-∞,3]∪[6,+∞)

D.[3,6]

图4

解：目标函数=表示点O(0,0)与可行域内的点P(x,y)连线的斜率。如图4,画出可行域。由得

A;由得B(1,6)。当直线O P过点A时,取得最小值为;当直线O P过点B(1,6)时,取得最大值为6。故选A。

三、已知线性约束条件为参数形式,求线性目标函数的最值问题

例3在约束条件下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是( )。

A.[6,15] B.[7,15]

C.[6,8] D.[7,8]

解：根据约束条件可画出可行域,如图5所示。

图5

目标函数z=3x+2y,即y=-,可知当斜率为的直线在y轴上截距最大时,z取得最大值。当s=3时,可知当函数经过C(1,2)时,z取到最大值7;而当s=5时,可知当函数经过B(0,4)时,z取到最大值8。所以z的最大值的变化范围为[7,8]。故选D。

点评：本题考查利用可行域求目标函数的最值,解决此类问题的一般步骤是：(1)作出可行域;(2)找到目标函数取最优解时的对应点;(3)将最优解的坐标代入目标函数即可求出最值。

变式训练3：若x、y满足且z=y-x的最小值为-4,则k的值为( )。

解：z=y-x表示在y轴上截距为z且平行于y=x的直线,z取得最小值-4时,得到直线y=x-4。画出直线x+y-2=0和y=x-4,由题意知,直线z=y-x经过原不等式所表示的平面区域的右端点(4,0),从而可知原不等式表示的平面区域如图6阴影部分所示。所以直线k x-y+2=0表示在x轴上的截距为4,在y轴上的截距为2的直线,当y=0时,x==4,k=,故选D。

图6

四、已知最优解成立条件，求线性目标函数参数的范围问题

例4已知变量x、y满足约束条件若目标函数(z=a x+ya＞0)仅在点(3,1)处取得最大值,则a的取值范围为

解：如图7,在坐标系中画出可行域。四边形A B C D,其中A(3,1),kA D=1,kA B=-1,目标函数z=a x+y(其中a＞0)中的z表示斜率为-a的直线系中的截距的大小。若仅在点(3,1)处取得最大值,则斜率应小于kA B=-1,即-a＜-1。

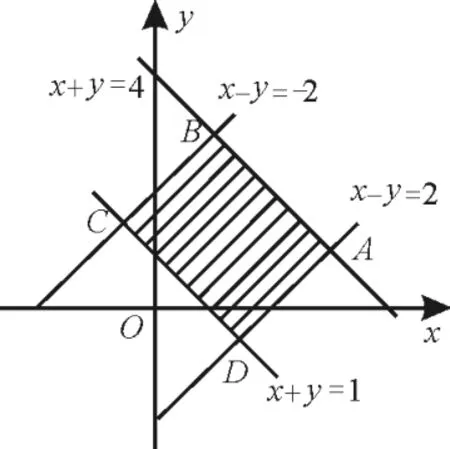
图7

所以a的取值范围为(1,+∞)。

点评：用图解决线性规划问题时,若目标函数z=a x+y只在点A处取得最优解,则过点A的直线z=a x+y与可行域只有一个交点,由此不难给出直线斜率-a的范围,进一步给出a的范围,但在解题时要注意目标函数是取最大值还是最小值,这也是这种题型最容易出错的地方。

变式训练4：已知x、y满足约束条件,使z=x+a y(a＞0)取得最小值的最优解有无数个,则a的值为( )。

A.-3 B.3 C.-1 D.1

解：如图8,作出可行域。作直线l：x+a y=0,要使目标函数z=x+a y(a＞0)取得最小值的最优解有无数个,则将直线向右上方平移后与直线x+y=5重合,故a=1,选D。

图8

五、求整数最优解问题

例5已知x、y满足约束条件,求z=7x+5y的最大值。

图9

解：满足线性约束条件的可行域如图9中的四边形A D O E内部的整点及部分边界整点。通过画图发现直线4x+3y-20=0,x-3y-2=0的交点是理论最优解,对应目标函数的理论最大值。但由于A不是整数点,故不是最优解。在可行域内所有整点有：(1,1),(1,2),(1,3),(1,4),(1,5),(2,1)(2,3),(2,4),(3,1),(3,2),(4,1),其中可使目标函数值较大的有(1,5),(2,4),(3,2),(4,1)(这些点也是距直线l0：7x+5y=34较近的点),代入目标函数一一验算,可知当x=2,y=4时,z有最大值34。

点评：如果可行域内整数点是有限的,我们可以写出可行域内所有整数点,然后再一一代入目标函数,通过验算,求出整数最优解。当可行域内含有无数个整点或整点较多时,这种方法就难以进行了。但可以改进,将接近的整数点逐个代入目标函数,通过验算,求出整数最优解。

变式训练5：给定区域令点集T={(x0,y0)∈D|x0,y0∈Z,(x0,y0)是z=x+y在D上取得最大值或最小值的点},则T中的点共确定条不同的直线。

解：如图10,阴影部分即为可行域。易得使z=x+y取得最小值的点仅有一个(0,1),使z=x+y取得最大值的点有(0,4),(1,3),(2,2),(3,1),(4,0)。点(0,1)与(0,4),(1,3),(2,2),(3,1),(4,0)中的任何一个点都可以构成一条直线,有5条。又(0,4),(1,3),(2,2),(3,1),(4,0)都在直线x+y=4上,故T中的点共确定6条不同的直线。

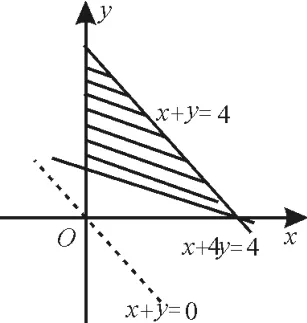
图10

六、线性规划的实际应用问题

例6A,B两种规格的产品需要在甲、乙两台机器上各自加工一道工序才能成为成品。已知A产品需要在甲机器上加工3小时,在乙机器上加工1小时;B产品需要在甲机器上加工1小时,在乙机器上加工3小时。在一个工作日内,甲机器至多只能使用11小时,乙机器至多只能使用9小时。A产品每件利润300元,B产品每件利润400元,则这两台机器在一个工作日内创造的最大利润是元。