基于并行卡尔曼滤波的车辆环境感知方法
2018-12-08涂岩恺张东风林明曹辉标
涂岩恺,张东风,林明,曹辉标
(1.厦门雅迅网络股份有限公司,福建厦门 361008;2.郑州宇通客车股份有限公司,河南郑州 450016)
0 引言
智能汽车是一个集环境感知、规划决策、多等级辅助驾驶等功能于一体的综合系统。它能使车辆在行驶过程中具有实时感知自身状态及所处地理环境的能力,能够为汽车的智能化动力性、安全性或经济性控制决策提供有力的参考依据。载荷与地理坡度是汽车智能优化控制最为依赖的感知量,目前针对载荷进行车辆优化控制的方法有发动机多态控制[1]、路径优化[2]等,针对地理坡度优化控制的方法有自适应巡航[3]、发动机功率控制[4]等,还有综合载荷与地理坡度的自动驾驶技术[5]。
传统的车辆环境感知都是基于传感器[6-7]的测量,但是高精度传感器面临成本高、易损坏、不易维护的问题。目前国外开始研究运用软件算法分析发动机和仪表往车辆总线上发出的实时数据推算出车辆当前载荷或所处地理坡度的方法。D KIM等[8]提出一种利用汽车纵向动力学关系和迭代最小二乘法的车身质量估算方法,但该方法易受坡度的影响。SEBSADJI等[9]提出利用扩展卡尔曼和龙伯格观测器结合的坡度估算方法,但是该方法以车身质量已知为前提,在实际商用车使用条件下,车身载荷的变化是非常大的。综合来看,目前缺少比较准确的能同时求解载荷与坡度的方法。
本文作者提出利用车辆CAN总线上的动力数据,采用分步骤方式先对状态方程进行差分来抵消相邻状态的坡度因素,并采用多组卡尔曼滤波器并行迭代处理,根据收敛结果误差最小的标准,来选择一组滤波器求解车辆总质量,之后再根据所求解的车辆质量利用纵向汽车模型来实时估算汽车所处的地理坡度。
1 系统数学模型
汽车纵向动力学模型如图1所示,汽车在行驶过程中同时受到外部力和内部力的作用。外部力包括空气阻力Fair、滚动阻力Frolling和重力Fgravity;内部力包括发动机输出的旋转扭矩经过传动系到达车轮上的前进驱动力Ftractive,以及传动系统的内部损耗。
根据图1所示的汽车纵向动力学模型,假设m表示汽车总质量,a为汽车加速度,则汽车的力学平衡关系:
Ftractive-Fair-Frolling-Fgravity=ma
(1)
汽车动力传动系统模型如图2所示。包括发动机、离合器、变速器、主减速器、车轮。发动机输出扭矩为Te,传动到离合器输出轴的扭矩为Tt,变速箱输出轴扭矩为Tf,轮轴扭矩为Tw。
发动机输出到变速器的扭矩Tt:
(2)
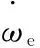
(3)
式中:It是传动惯性;it是传动挡位比;Tf是通过变速器后的输出扭矩。Tf通过主减速器,最终转化为轮轴上的驱动扭矩Tw:
(4)
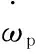
(5)
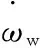
(6)
车辆的加速度可以表示成车轮的旋转加速度乘以车轮的半径:
(7)
综合上述公式可以得到牵引力的表达式:
(8)
式中:ug=itf/rw。
汽车行驶时纵向空气阻力:
(9)
式中:ρair是空气密度;Cd是空气阻力系数;A是车正面的面积。
汽车行驶时的纵向滚动阻力:
Frolling=frmgcosθ
(10)
式中:fr是滚动阻力系数;g是重力加速度常量;θ是道路坡度。
汽车行驶时由坡度带来的阻力:
Fgravity=mgsinθ
(11)
将公式(8)—(11)代入到公式(1)中,并且令βr=cos[arctan(fr],整理可得到:
(12)
式(12)可视为一个描述发动机输出扭矩、车速与质量、坡度关系的非线性方程。后续将该方程作为状态方程,联立观测方程,采用卡尔曼滤波迭代的方法,利用连续采集的车辆CAN总线动力数据(包含扭矩Te和车速v)对汽车总质量和坡度求解。
2 状态方程与求解
令Ts为车辆两个状态的时间间隔,v表示车辆速度,下标k表示状态序号,基于式(12)建立基于车辆速度的状态方程如下:
(13)
如果直接采用扩展卡尔曼滤波方法同时迭代求解式(13)状态方程中的坡度和质量参数,容易陷入错误收敛。例如当车辆行驶在无坡度的平原地区时,因为无地形变化来纠正误差,有可能迭代收敛得出质量偏重地形长下坡、或质量偏轻地形长上坡的错误结论。文中提出将状态方程进一步差分、分步求解的方法,先利用多组卡尔曼滤波器进行并行计算,取收敛后预测噪声最小的一组滤波器的质量作为车辆当前质量,再反推车辆所处的地理坡度。因为车辆总线上速度信号和扭矩信号的发送频率非常快,前后两个信号周期一般在100 ms以内,因此,前后两个状态的坡度和道路阻力系数近似相等,即:α2φ2,k≈α2φ2,k-1,因此将式(13)前后两个状态相减,令Xk=vk-vk-1,整理可得抵消掉坡度参数只含质量参数的状态方程:
Xk=AXk-1+BUk+Wk
(14)
式中:A=1;B=Ts;
观测量即为车辆当前的纵向加速度,因此观测方程:
zk=HXk+Vk
(15)
式中:观测矩阵H=1;Vk为观测噪声,方差为R。Pk表示信号协方差,即信号的预测误差。建立卡尔曼迭代方程组如下,其中ε取一个常数初始值开始迭代:
(16)
上述迭代方程组是对车辆加速度的预测求解,且方程组中的质量参数未知,不能直接进行运算,需要有一个预设质量值。由于商用车辆的车型参数中具有空载的整备质量me与最大允许总质量mz两个参数,因此实质的载重质量应该介于me与Mz之间。在me与mz之间每100 kg取一个质量值,作为式(16)迭代方程组中的质量参数,这样一共有N=(mz-me)/100组卡尔曼迭代方程组进行并行计算。N组卡尔曼滤波器各自独立进行迭代运算,如图3所示。
取所有运算结果为收敛的滤波器,比较收敛后Pk的大小,Pk越小,表示使用当前质量对于加速度的预测误差越小,说明该质量参数最符合车辆运行的动力模型,取该组卡尔曼滤波器对应的质量值为车辆当前总质量。求得车辆质量参数后,将质量代回公式(12)即可由车辆的扭矩信号Te及加速度a计算车辆当前所处坡度值。
3 实验结果
采用ZK6876H5Z型号客车进行实验,整备质量为4 300 kg,最大允许质量为6 100 kg。实验时经过装载负重,实际整车质量为5 543 kg。由于比较难去测绘准确的道路地理坡度,因此将车辆置于汽车转鼓实验台上进行实验,如图4所示,所需地理坡度可直接在转鼓实验台上设置,将文中的环境感知算法计算得到的坡度与转鼓所设地理坡度比较,以验证数据的准确性。
从整备质量4 300 kg开始,每100 kg取一个质量代入式(16)卡尔曼滤波器组,一共有19组滤波器并行进行迭代计算,每组滤波器ε取一个相同常数初始值,进行了200轮迭代后,共有4组滤波器收敛,15组滤波器不收敛。收敛的4组滤波器Pk值关系如图5所示。
可以看到,5 500 kg对应的卡尔曼滤波器迭代收敛误差最小,因此取5 500 kg为载重计算结果。得到质量之后,进一步反推车辆所处的坡度。将利用式(12)反推出的车辆所经过的地理坡度和转鼓设置的坡度进行对比,结果如图6所示,可以看出二者有比较高的重合度,说明此方法估算的地理坡度有比较高的准确性。
4 小结
文中通过车辆的纵向动力学关系,在建立基于速度的状态方程基础上,进一步进行差分处理,建立基于加速度的卡尔曼迭代计算方程,利用汽车总线信号频率高间隔短的特点,先约去卡尔曼滤波器中的坡度参数,将质量参数分段代入滤波器组中,利用并行卡尔曼滤波器组迭代计算,选择收敛后误差最小的滤波器组对应的质量为估算的车辆质量,之后再反推坡度。实验证明:该方法有比较高的准确性,可直接利用车辆总线信号估算车辆环境参数,减少了利用传感器的成本,使车辆能够实时感知当前所处内外部环境状态,能有效提高车辆智能化水平。
