车用燃料电池欧姆内阻辨识算法

曾雷，符兴锋，任强，张松林，翟艳霞，王佳骐

(广州汽车集团股份有限公司汽车工程研究院，广州广东 511434)

0 引言

燃料电池是一种把燃料所具有的吉布斯自由能部分转换成电能的装置，它分为碱性燃料电池、磷酸燃料电池、固体氧化物燃料电池、质子交换膜燃料电池(Proton Exchange Membrane Fuel Cell, PEMFC)。其中PEMFC以氢作为燃料，具有功率密度高、体积小、质量轻、反应温度适中、启动速度快、比能量高等优点，是21世纪最有前途的“绿色能源”装置[1]，被认为是实现未来汽车工业可持续发展的重要方向之一[2]。

对于PEMFC来说，欧姆内阻是其运行的一个重要参数，它反映了燃料电池内部的运行状态[3]，是衡量质子和电子在电池内部传输难易程度的主要标志，体现发电效率的大小[4]。另外，通过估计欧姆内阻可以间接地预测膜的湿度和电池寿命的衰减。文献[5-6]中采用交流阻抗法测量燃料电池的内阻，该方法对燃料电池的扰动比较小，但也需要额外的激励源。文献[7]中采用改进型交流阻抗法测量燃料电池的内阻，但仍然需要额外的激励源。文献[3]中则采用双卡尔曼滤波算法估计燃料电池欧姆内阻，只需输入燃料电池电压电流数据即可实时辨识出燃料电池欧姆内阻，但双卡尔曼滤波算法相对较复杂。本文作者采用最小二乘法，根据燃料电池电压电流数据实时辨识燃料电池欧姆内阻。

1 燃料电池等效电路模型

1.1 燃料电池工作原理

PEMFC由阳极、阴极和质子交换膜组成，基本原理如图1所示。工作时，氢气和氧气发生反应形成离子移动，从而在外部电路形成电流。阳极发生氧化反应，电子流流向外部电路，氢离子穿过质子交换膜到达阴极：

H2→2H++2e

(1)

阴极发生还原反应，氧气与氢离子结合产生水：

(2)

电池总反应：

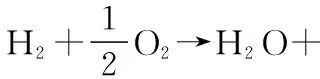
(3)

图1 PEMFC基本原理

1.2 燃料电池工作原理

文献[8]中同时考虑燃料电池内阻容性和阻性的特点，提出的电池内部电路模型如图2所示，该模型由一个电阻和一个阻容并联环节组成。

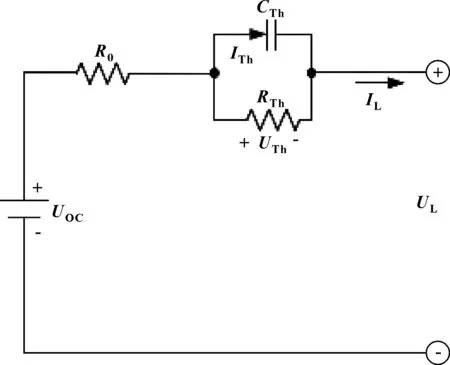
图2 燃料电池内部电路模型

模型中电阻R0即是所求的欧姆内阻，由于该电阻的存在，当电流IL发生突变时也会引起输出电压UL的突变，由双电层分布电容CTh和电阻RTh组成的RC并联环节，体现了燃料电池电极表面多孔结构的化学特性[3]。燃料电池能斯特电压与氢气压力、氧气压力以及温度等多种因素有关，实际得到的开路电压要比理论计算得到的能斯特电压小[3]。模型中的UOC可理解为燃料电池的开路电压，在燃料电池正常工作区域(线性区域)可视为定值。

1.3 等效电路模型的差分方程

根据电路相关知识可列出等效模型的数学关系如下：

(4)

下面推导该模型的差分方程，将公式(4)离散化得

(5)

式中：Δt为采样间隔；τ为时间常数；k为采样时刻。令Ek为k时刻的动态电压：

Ek=UL,k-UOC,k

(6)

由公式(5)和(6)可得

Ek+1=-[e-Δt/τUTh,k+(1-e-Δt/τ)RThIL,k]-IL,k+1R0=

-[e-Δt/τ(UOC,k-UL,k-IL,kR0)+(1-e-Δt/τ)RThIL,k]-IL,k+1R0=

e-Δt/τEk+(-R0)IL,k+1+[e-Δt/τR0-(1-e-Δt/τ)RTh]IL,k

(7)

因此，差分方程可以写成：

Ek+1=aEk+bIL,k+1+cIL,k

(8)

式中：a、b、c为待估计参数，a、b、c分别为

(9)

由公式(9)可知，只要能辨识出差分方程的参数b，就可以求出电池等效模型的参数R0，即燃料电池的欧姆内阻。

2 利用最小二乘法辨识欧姆内阻

2.1 离线最小二乘法

最小二乘法是一种古老的数据处理方法，由高斯首先提出最小二乘法的概念，并将它用于天文计算。在参数辨识领域中，最小二乘法是重要的估计方法。它既可以用于动态系统也可用于静态系统，既可用于线性系统也可用于非线性系统，既可用于离线估计也可用于在线估计。在随机的环境条件下，利用最小二乘法时，并不要求观测数据提供出有关噪声的概率统计特性，而这种方法所得出的结果却有相当好的统计特性。下面对最小二乘法基本原理进行简要介绍，假设被辨识系统的差分方程：

z(k)=-a1z(k-1)-......-anz(k-na)+b0u(k)+b1u(k-1)+......+bnu(k-nb)+e(k)

(10)

式中：z(k)为系统输出量的第k次观测值，z(k-1)是系统输出量的第k-1次观测值，依次类推；u(k)为系统的第k次输入值；e(k)为均值为零的噪声；a1、......、an，b1、......、bn为待辨识参数。

令：

(11)

式中：h为样本集合；θ为待辨识参数向量，则式(10)可改写为

z(k)=hT(k)θ+e(k)

(12)

对于k=1,2,......，G，构成了一个线性方程组，可以写成：

zG(k)=HG(k)θ+eG(k)

(13)

式中：

(14)

HG=

(15)

最小二乘法的基本思想是找出一个参数估计值θ，使得判定函数：

(16)

取极小值，此时的参数估计值称为最小二乘法意义下的估计值，用θGS表示，可以推出：

(17)

2.2 递推最小二乘法及欧姆内阻辨识

上一节讨论的最小二乘算法是一种离线算法，适合成批处理观测数据。为了实时跟踪动态系统的时变参数，需转化成递推算法。递推算法的基本思想是当被辨识系统在运行时，每获得一组新的观测数据后，在上次估计结果的基础上，利用新获取的观测数据对上次估计的结果根据递推算法进行修正，从而递推得到新的参数估计值。这样随着新的观测数据的逐次引入，不断地进行参数估计，直到参数估计值接近于真实值。递推最小二乘算法的基本思想可以概括：

此次新的估计值=上次老的估计值+修正项

即新的估计值是在老的估计值的基础上，利用新的观测数据对老估计值进行修正而得到的。假设上次老的估计值：

(18)

则此次新的估计值：

(19)

令：

(20)

则可以推出：

(21)

整理得到最小二乘法的递推公式：

(22)

最小二乘算法的推导中，没有做任何近似处理。因此，递推估计和离线估计在理论上是一致的。结合公式(8)电池模型的差分方程，可知：

(23)

式中：Ek=UL,k-UOC,k，开路电压UOC,k在燃料电池正常工作区域可视为定值，给定初始值P0和θGS,0(后面章节有初始值设定分析)，再输入燃料电池两端电压、电流值即可实时辨识出a、b、c3个参数。根据公式(9)可知欧姆内阻为-b，从而得到电池的欧姆内阻。

3 算法分析及验证

3.1 欧姆内阻辨识

文中采用广汽某款燃料电池车上的电堆，额定功率30 kW，由120片单体串联而成，工作电流0～500 A，工作电压60～120 V，开路电压105 V。文中搭载NEDC(New European Driving Cycle)工况进行算法的分析及验证。NEDC是新欧洲行驶工况，主要有欧洲、中国、澳大利亚等国家使用，由市区运转循环和市郊运转循环组成，其电压电流曲线如图3所示，采样间隔为0.2 s。

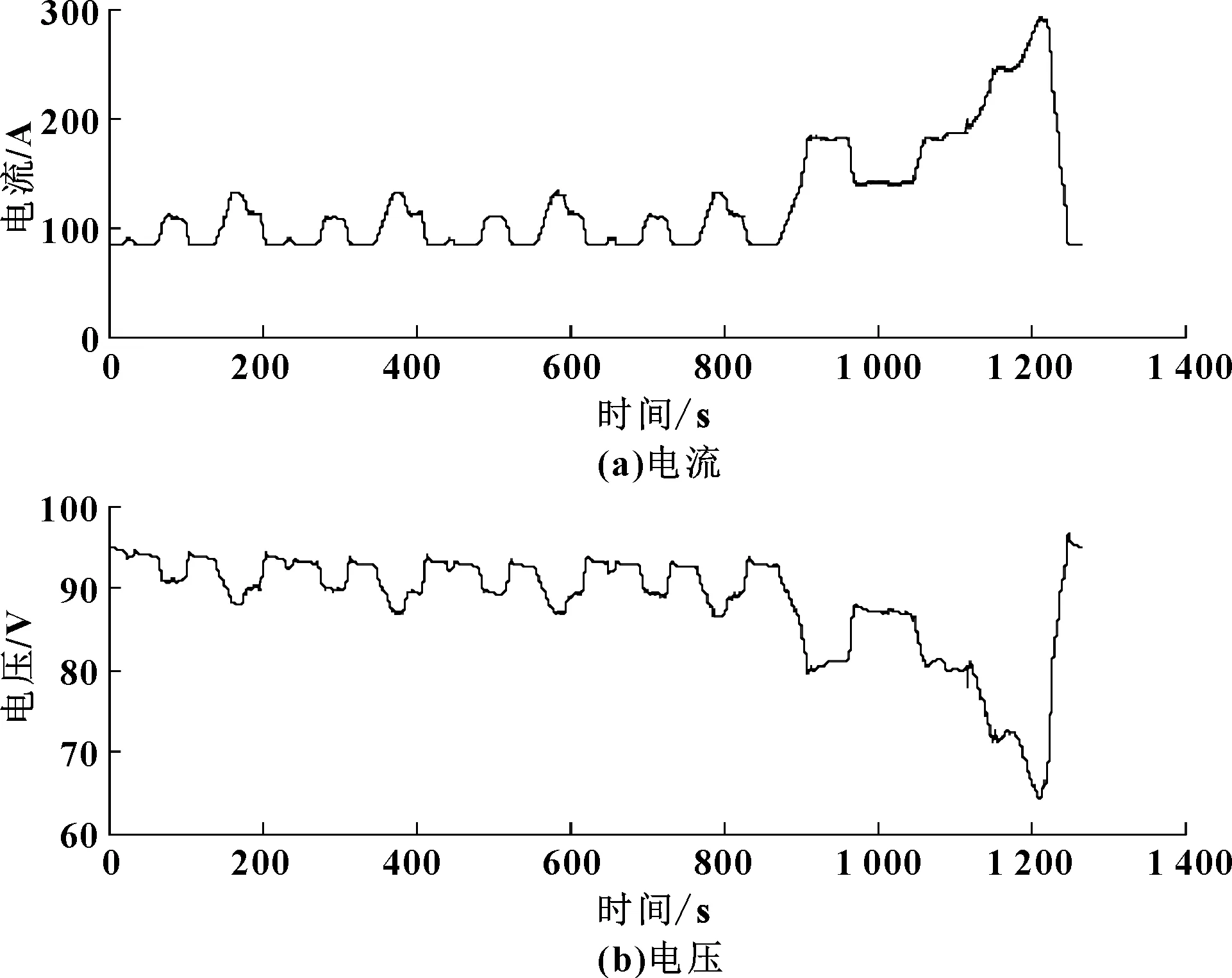
图3 NEDC工况电压电流曲线

给定初始值如下：

θGS,0=[1, 1, 1]T×m

(24)

式中：n为1×106；m为0。实时辨识出的欧姆内阻曲线如图4所示。可以看出：在辨识初期结果波动比较大，这是因为算法在辨识初期还未收敛，之后曲线逐渐稳定，验证了算法的收敛性，最终的辨识结果为0.037 9 Ω。

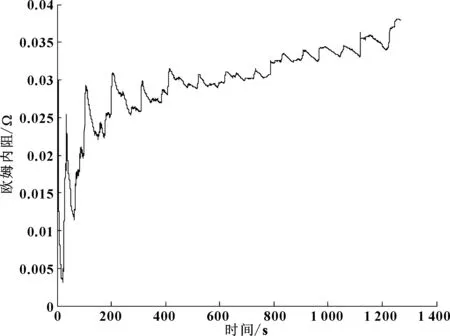
图4 欧姆内阻辨识结果

3.2 算法验证

燃料电池的可测量较少，常用的参数辨识准确与否的验证方法是利用真实电压输出与辨识得到内部参数值之后，利用辨识参数值导入仿真模型得到的电压输出值，两者相比较可以得出参数辨识算法对电池内部参数的辨识能力，两者之间的误差值越小，则辨识算法越准确，这是目前较为常用的参数辨识算法的评价方法。在Simulink仿真平台上搭建好验证模型，如图5所示，输入电流、真实的电压以及开路电压值，利用递推最小二乘法估计出欧姆内阻，然后反推出仿真电压值，再结合真实电压值得出电压误差曲线。电压误差如图6所示，可以看出：整个辨识过程中电压误差值始终在±1.5 V以内，相对开路电压误差为1.4%，验证了算法的有效性。

3.3 算法初始值的设定

对于上述算法，在开始计算的第一步必须给定P0和θGS,0的初始值，表1是不同初始值对应的估计结果，m、n含义见上文所述。

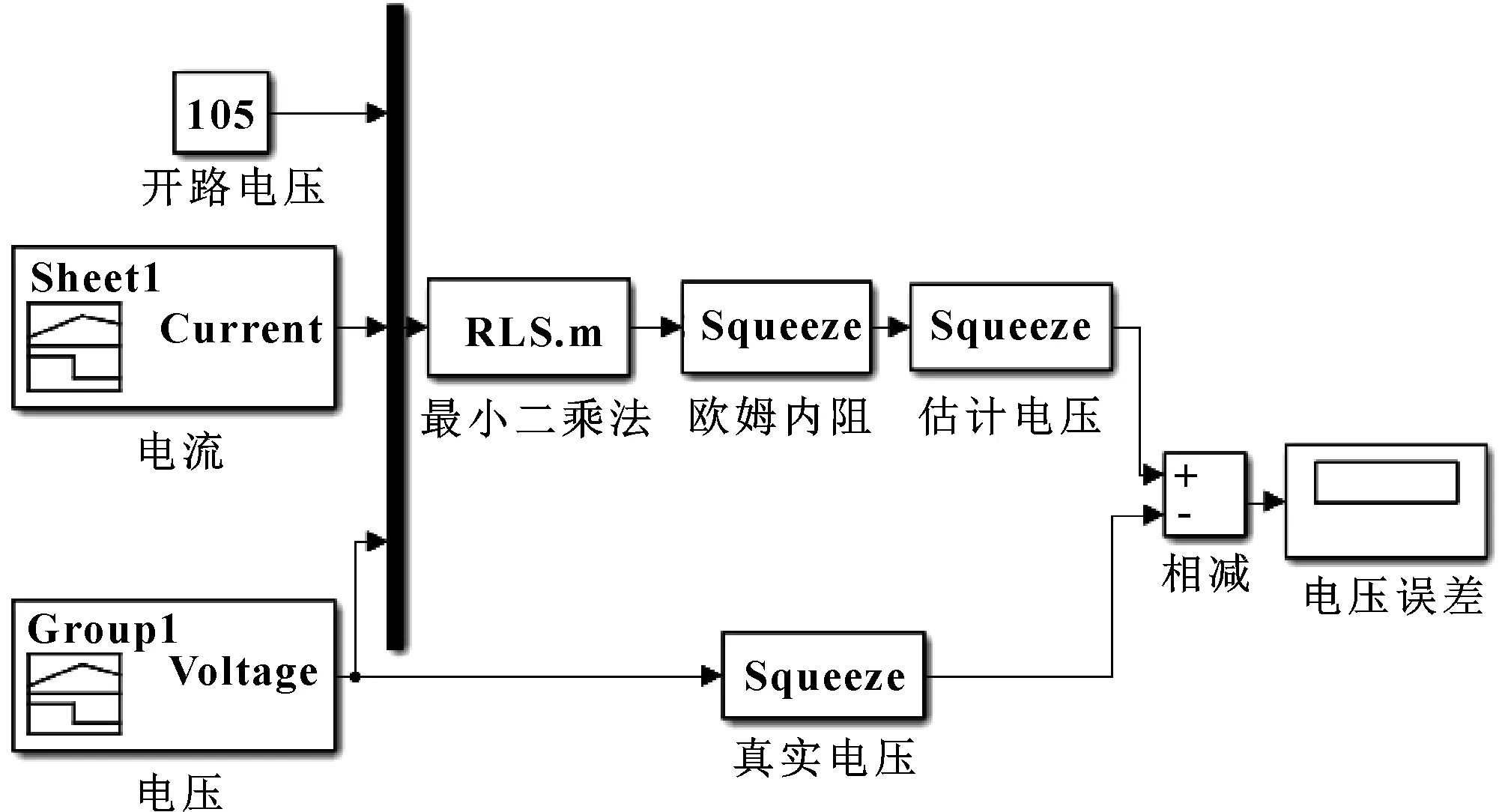
图5 验证模型

图6 电压误差结果

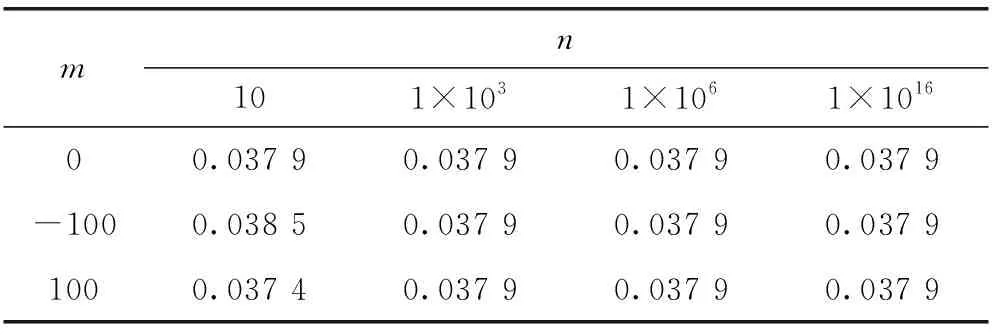
mn101×1031×1061×101600.037 90.037 90.037 90.037 9-1000.038 50.037 90.037 90.037 91000.037 40.037 90.037 90.037 9

从表中可以看出：当n的取值足够大时(1 000以上)，初值的设定对估计结果无影响。当n初始取值10时，m初始值-100和100对应的相对误差也仅为1.6%和1.3%，在可接受范围内。因此，初始值的选定对估计结果影响很小，当n取值足够大时，初值对估计结果的影响基本可以忽略。由此可见，算法具有良好的鲁棒性。

4 结束语

文中基于质子交换膜燃料电池的等效电路模型，提出采用最小二乘法辨识电池的欧姆内阻，所提出的方法与现有方法相比，具有在线实时估计、无需额外激励源以及硬件电路支持、算法较简单等优点，而且通过搭载整车NEDC工况，在Simulink仿真平台上验证了该算法的收敛性、有效性以及良好的鲁棒性。当然，该算法仅仅适用于燃料电池在线性工作区域内，结合实车数据，可以发现燃料电池大部分时间都工作在线性区域，因此并不影响此方法的推广。对于PEMFC来说，欧姆内阻反映了燃料电池内部的运行状态，是衡量质子和电子在电池内部传输难易程度的主要标志，体现发电效率的大小。另外，通过估计欧姆内阻可以间接地预测膜的湿度和电池寿命的衰减。由于电堆中各单体本身存在差异性以及电堆装配工艺的原因，单体电池的输出特性存在不一致，而单片电池的性能会直接影响到整个电堆的性能。因此，辨识出的欧姆内阻可应用于：(1)间接估算膜的湿度，为加湿策略提供参考；(2)间接估算电堆的健康状态，从而预测电堆寿命；(3)估算电堆输出功率、发电效率等状态参数；(4)辨识出单体的欧姆内阻可判断电堆的不一致性，从而及时采用相应措施。