基于扩展卡尔曼滤波的车用锂离子电池SOC估算

何忠霖，彭忆强，郭威,席林

(西华大学汽车与交通学院，四川成都 610039)

0 引言

随着国家对环保的要求越来越严，督查力度愈来愈大，不少系统和设备开始采用锂离子电池作为能量的主要来源。锂离子电池具有能量密度大、功率密度大、自发放电率低、无记忆效应等优点。荷电状态(State of Charge， SOC)作为电池管理系统(Battery Management System， BMS)中均衡各单体电池的重要参数，在动力电池的使用过程中，易受到内外各种不确定因素的干扰，发生复杂电化学反应的锂离子电池又是典型的非线性系统。因此，如何利用电池可测参数数据，如电流、电压、温度、自放电率、循环充电次数等，通过适当算法来实现当前电池剩余电量准确估算，一直以来是BMS的核心问题和亟需解决的技术难点。为适应需求，许多估算方法应运而生。文献[1]中提出了安时积分法，并分析了安时积分法估算SOC存在的误差及解决方案；文献[2]中提出了开路电压法，并得到了开路电压法不适于SOC在线实时估算的结论；文献[3]中提出了有效质量法，通过测量电池电解液有效质量估算SOC值，但该法只适用于能直接测量电解液质量的铅酸电池，对于纯电动汽车主要使用的锂离子电池，并不具备使用价值。基于现代控制理论而提出的SOC估计策略在近年来得到了长足发展，其中主要的方法有卡尔曼滤波法、神经网络法、状态观测器法等[4]。其中，神经网络估算和模糊控制法由于难度大，还停留在计算机仿真研究阶段，距离实际运用还有不少路要走。

电池组电量一般是按照电池模组总电压来进行估算和矫正的，如果电池组的不一致性很大，将会使SOC估算精度误差增大。具有代表性的是韩国亚洲大学和先进工程研究院，研究人员在对镍氢电池SOC估算过程中，提出了考虑自恢复效应、自放电效应及老化效应对电池容量的影响[5]，并提出SOC计算公式：

SOC(%)=100%×(实际容量+自恢复效应恢复电量-自放电效应放电量-老化效应损失电量+充电量-放电量)/额定容量

(1)

该公式考虑了伴随电池使用导致的老化效应，存放过程中的自放电效应和充、放电结束时的自恢复效应对电池电量的影响，计算所得SOC精度相对较高。

对于电动汽车，SOC估算准确与否在很大程度上取决于电池本身寿命长短。同时，SOC也作为电池最基本信息之一提供给驾驶者。因此，SOC估算是BMS中的重点和难点。

为适应锂电池复杂电反应机制，本文作者在卡尔曼滤波的基础上，通过将扩展卡尔曼滤波(EKF，Extended Kalman Filter)和复合电池模型结合，搭建了基于EKF原理下SOC估算的仿真模型。文中的创新点在于考虑到复合电池模型的输入参数为充、放电电流和电池温度，添加了与电池温度有关的容量校正模型和与库仑效率有关的电流效率模型，实现对SOC估算的校正，增加模型估算精度。

1 扩展卡尔曼滤波

1960年卡尔曼在时域状态空间理论基础上提出了卡尔曼滤波，随着计算机系统的发展，卡尔曼滤波逐渐应用到控制系统的各个领域。在卡尔曼滤波中，状态方程表示相邻时刻状态变量的变化规律，输出方程对部分或全部状态变量进行观测，从而实现系统状态变量的最优估计，即由初始化、估测估计及最优估计三部分构成。

标准卡尔曼滤波常用于线性动态系统，其状态空间模型如下：

状态方程：

xk+1=Akxk+Bkuk+wk

(2)

输出方程：

yk=Ckxk+Dkuk+vk

(3)

式中：uk为系统的输入量，输入量是电池温度和电流；xk为状态变量，代表SOC值；yk为输出量，指电池负载电压，也称端电压；vk为过程噪声，描述状态转移过程中的加性噪声及误差的过程噪声变量；wk为观测噪声，表示测量系统输入量时产生的噪声和误差，由于vk、wk均为高斯随机白噪声，在计算的过程中无法知道实际值，故将其假设为零；Ak、Bk、Ck、Dk为方程匹配系数，用来体现系统动态特性。

锂离子电池性能受到温度、电压、电流等多种因素的影响，在使用过程中是典型的非线性系统，应采用扩展卡尔曼滤波对电池组SOC进行实时估算。扩展卡尔曼滤波是通过系统状态空间模型将动力电池非线性系统进行线性化，然后再利用标准卡尔曼滤波算法的原理对状态变量做最优估计。系统状态空间模型如下：

状态方程：

xk+1=f(xk,uk)+wk

(4)

输出方程：

yk=g(xk,uk)+vk

(5)

式中：f(xk,uk)为非线性转移函数；g(xk,uk)为非线性测量函数。相对于标准卡尔曼滤波，扩展卡尔曼滤波用f(xk,uk)替代了Akxk+Bkuk，用g(xk,uk)替代了Ckxk+Dkuk。为方便理解，给出如图1所示的方框图。

图1 非线性离散时间状态模型

具体计算过程如下：

(6)

(7)

状态变量的真值无法直接测得，因此只能通过间接的方法通过计算得到，必然存在误差。扩展卡尔曼滤波正是将存在的误差利用最小均方差原理让最优估计经过有限次后收敛于真实状态值。因此，EKF计算后结果收敛的准确性与初值无关，初值仅决定收敛所需时间，而模型的精确性决定收敛结果精度。

(8)

(9)

式中：Dw是过程噪声wk的方差,会让均方估计值增加并且会增加状态估计值的不稳定性。

(3)卡尔曼滤波增益Lk：

(10)

式中：Ck为匹配系数，用来体现系统动态特性；Dv是观测噪声vk的方差。卡尔曼滤波增益又叫信噪比平衡因子。当状态变量处于比较稳定时，修整幅度较小，Lk值较小，反之Lk值较大，修正幅度较大。由公式(10)可以看出，当观测噪声增大，Lk值会减小，导致调整幅度减小。

(11)

(12)

当观测变量yk测量结束后，采用标准卡尔曼滤波对状态变量、均方估计误差的预测估计值进行修正，从而得到状态变量、均方估计误差的最优估计值。

2 电池模型

文中以某磷酸铁锂单体电池模组作为研究对象，基本参数如表1所示。对于扩展卡尔曼滤波，从非线性转移函数f(xk,uk)、非线性测量函数g(xk,uk)和状态变量的角度出发，可以分为复合模型、简化模型、带滞后效应模型、极化效应修正模型。虽然复合模型精度不及带滞后效应模型和极化效应修正模型，但计算较为简单且易于微控制系统实现，所以文中选择复合模型进行模型搭建。模型总体框架如图2所示。

表1 某磷酸铁锂电池模组参数

图2 系统结构框图

2.1 复合模型

复合模型是基于Shepherd模型、Unnewehr universal模型、Nerest模型组合得到[7]。

状态方程：

(13)

输出方程：

(14)

式中：ηT为温度对电池容量的补偿系数；ηI为库仑效率对电池容量的补偿系数；R为电池内阻，会随温度和充、放电状态变化；Ki为电池极化电阻，K1、K2、K3、K4是利用最小方差原理得到，为电池相关匹配参数。

2.2 温度对电池容量校正模型

电池内部温度是影响电池容量的重要因素。温度较高时，电池活性增加，能量得到更有效地发挥，但若电池在高温环境下长时间工作，会让电池中的电解质和某些活性物质发生不可逆转的化学反应，从而导致电池内部晶格被破坏，寿命明显地缩短。温度较低时，电化学反应速率降低，电池活性明显降低，温度过低时电解液甚至可能冻结，极化效应明显，电池内阻增加，电池很难充满电，实际可用容量减少，电池能量利用效率下降。

电池内部温度对SOC的影响主要有以下两点：(1)非线性特性。温度对SOC的影响是非线性的，无论大小，都不能用简单的线性关系进行描述。(2)温度对电池容量的影响是非固定的。因此，需要通过试验得到不同温度下的容量补偿系数。以某单体磷酸铁锂电池为研究对象，在满电(45 A·h)情况下，分别将电池置于-20、-10、0、 25、 40、60 ℃的温度下，以标称放电倍率C/30对电池进行放电到截止电压，通过实验可得到各温度下电池的实际容量，通过与标称容量比较，可得到不同温度下的容量补偿系数ηT：

(15)

式中：QTi为实际容量；QTI为标称容量。

具体数据如表2所示。

表2 不同温度下的补偿系数

由于所测点温度分别为-20、-10、0、 25、 40、60 ℃，其为离散点，不能为除所测点外的其他温度提供容量校正值。因此，将所测实际容量与对应温度进行曲线拟合，为其他温度下的容量校正提供支撑，如图3所示。

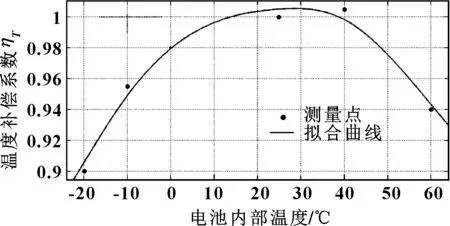
图3 内部温度对电池容量校正拟合曲线

一般电池测量温度为电池极柱温度，由于电池在生产过程中由于本身构造、使用材料以及装配方式等不同，导致电池内部温度和电池极柱温度有差异，所以需对所测电池温度进行自校。在满电并以C/30倍率进行放电，直至截止电压，如表3所示。

表3 不同温度下的自校系数

为得到除测量点外其他温度的自校系数εT，将表3所测数据进行曲线拟合，如图4所示。

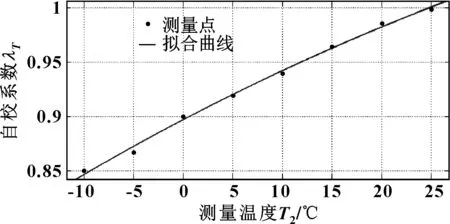
图4 温度自校系数拟合曲线

2.3 电流效率模型

电流效率模型主要与库仑效率有关。库仑效率又叫放电效率，是指在同一循环过程中放电容量和充电容量的比值。与磷酸铁锂电池不同的是，镍氢、镍镉蓄电池具有一定的耐过充能力，因此均衡策略常被设计为正限制。随着电量增加，磷酸铁锂电池的库仑效率会逐渐降低，过充的电能大部分转化为热能消散了。而磷酸铁锂电池的库仑效率一般能达到90%，应在建模过程中考虑该电池库仑效率变化对电池容量的影响。磷酸铁锂在实际使用过程中，充电过程一般是先恒流充电，充到截止电压后再恒压充，最后进行涓流充电，充电模式较为固定。因此，库仑效率主要考虑放电倍率的影响。设置充、放电条件：在25 ℃条件下，充电倍率为0.5C(22.5 A)，分别以0.1C(4.5 A)、0.5C(22.5 A)、1C(45 A)、1.5C(67.5 A)、2C(90 A)、3C(180 A)放电倍率进行放电至截止电压，如表4所示，可得到不同放电倍率下的容量补偿系数，即库仑效率ηI：

(16)

式中：Qti为实际放电容量；QtI为实际充电容量。

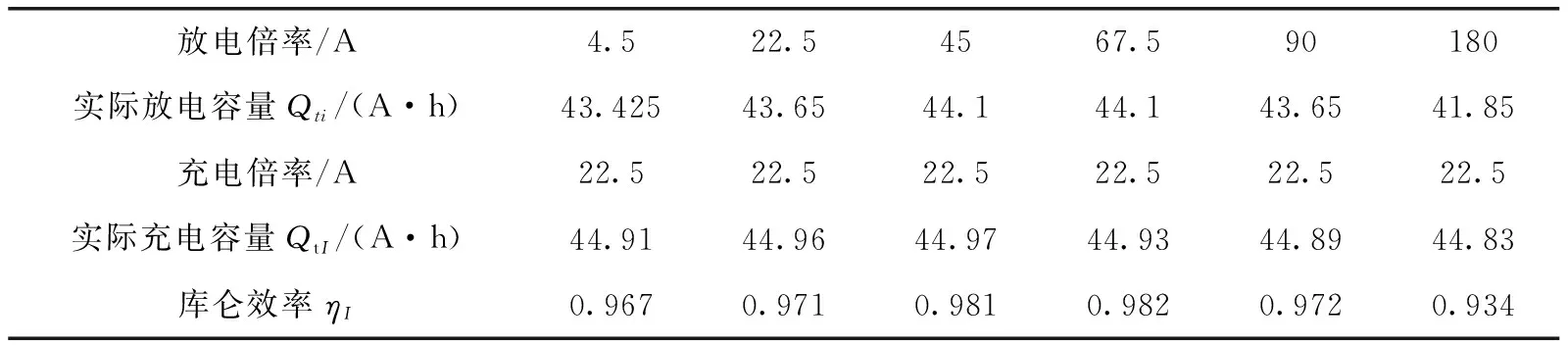
表4 不同放电倍率下的库仑效率

同理，为得到不同放电倍率下的库仑效率ηI，将表4中测量点拟合，得到如图5所示曲线。

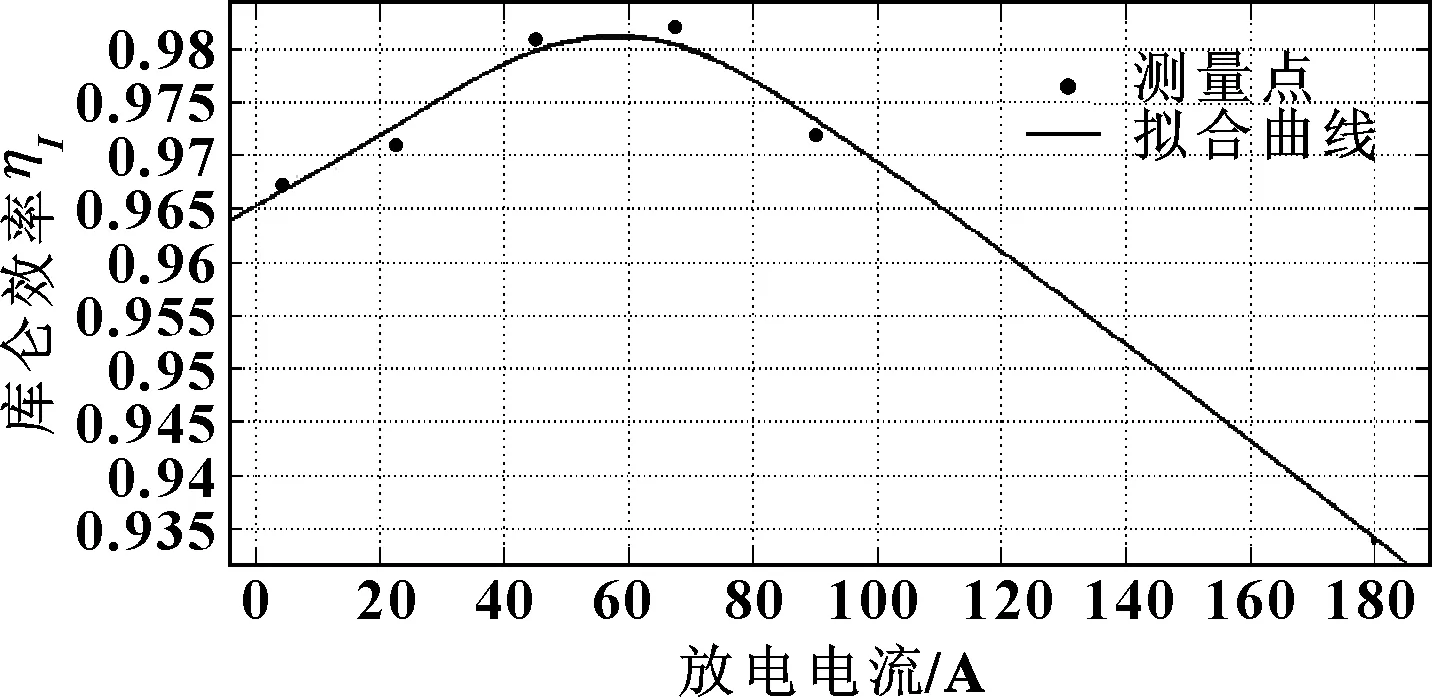
图5 库仑效率拟合曲线

3 仿真结果分析

模型搭建完成后，为考虑充、放电倍率对该算法SOC估算的影响，选择在常温(25 ℃)下，分别对该模型以1C、3.4C进行恒流放电，静置一段时间后，再分别以1C、3.4C进行恒流充电、放电，如图6—图7所示。下面将截取一部分数据，来验证文中所提算法的精确性。

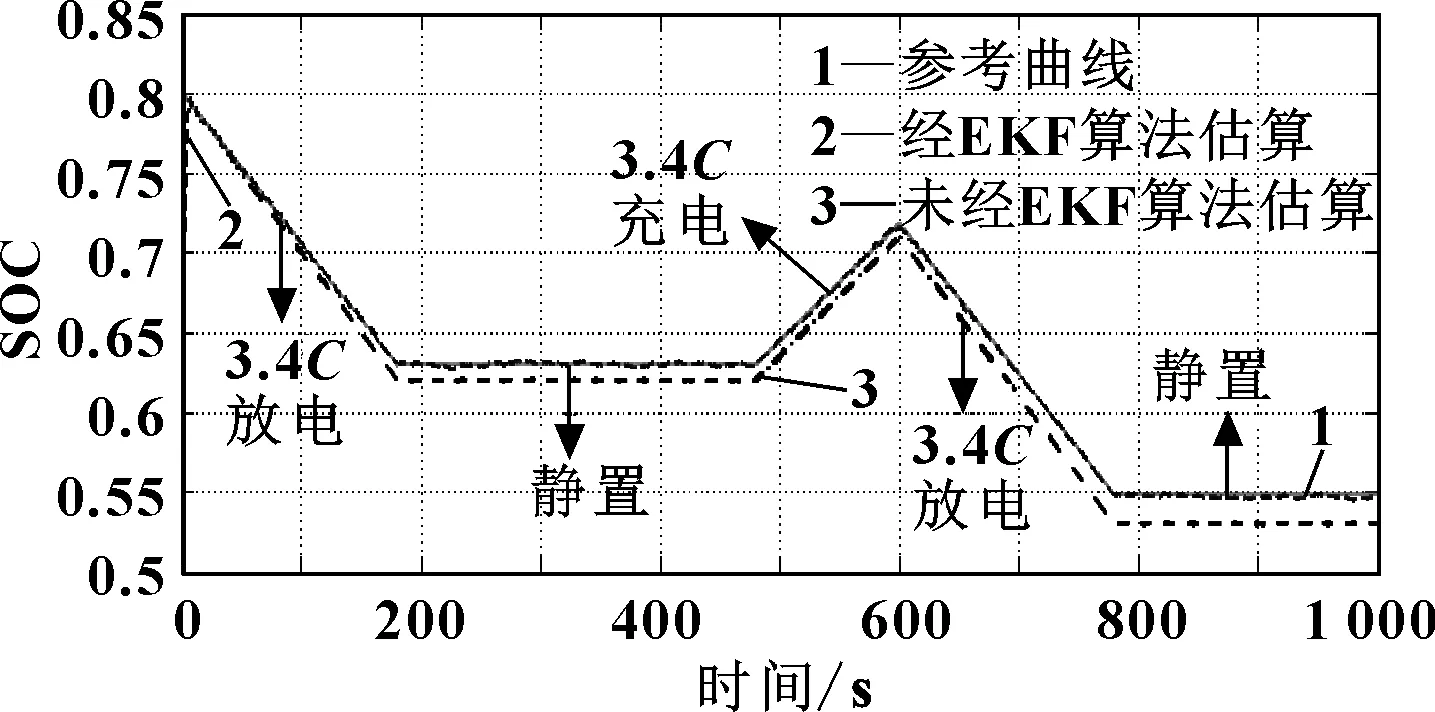
图6 25 ℃，3.4C充、放电倍率下SOC值曲线图

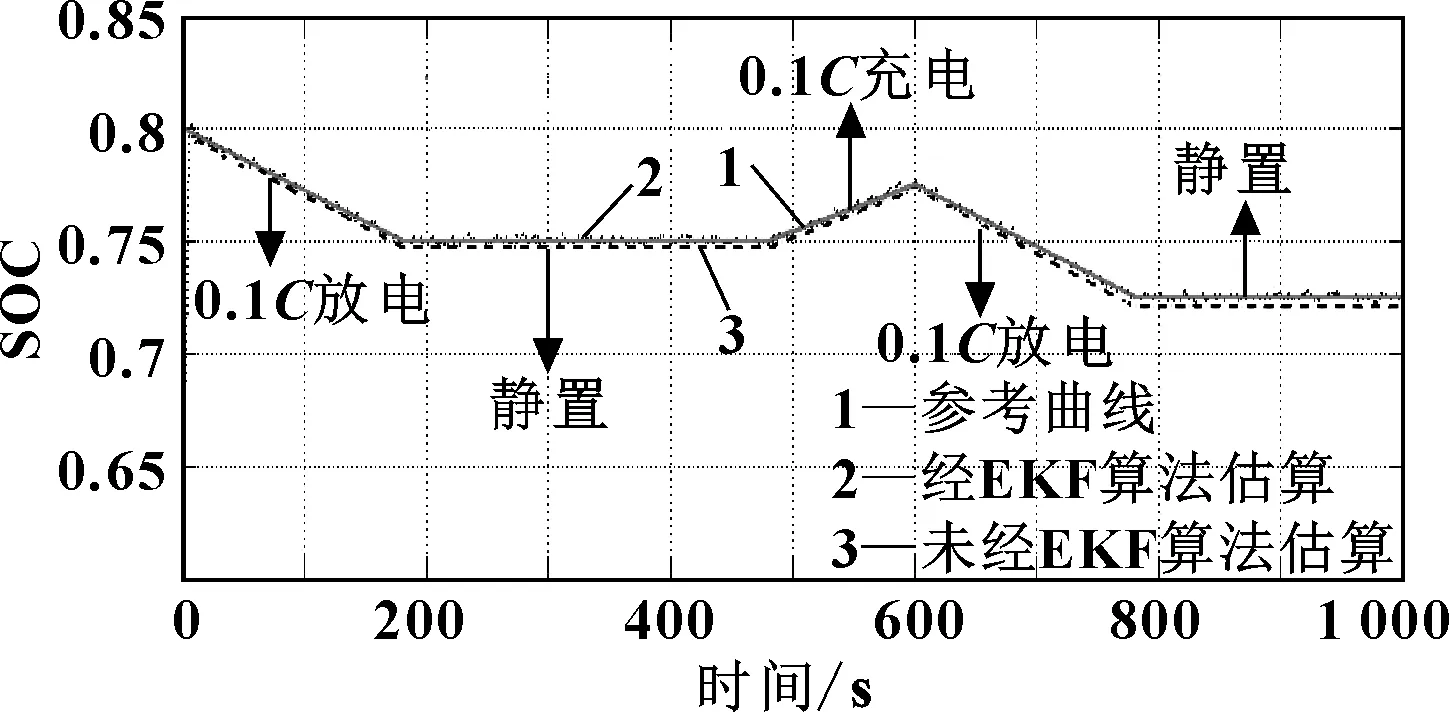
图7 25 ℃，1C充、放电倍率下SOC值曲线图

将1C充电倍率下的SOC曲线图局部放大，如图8所示。

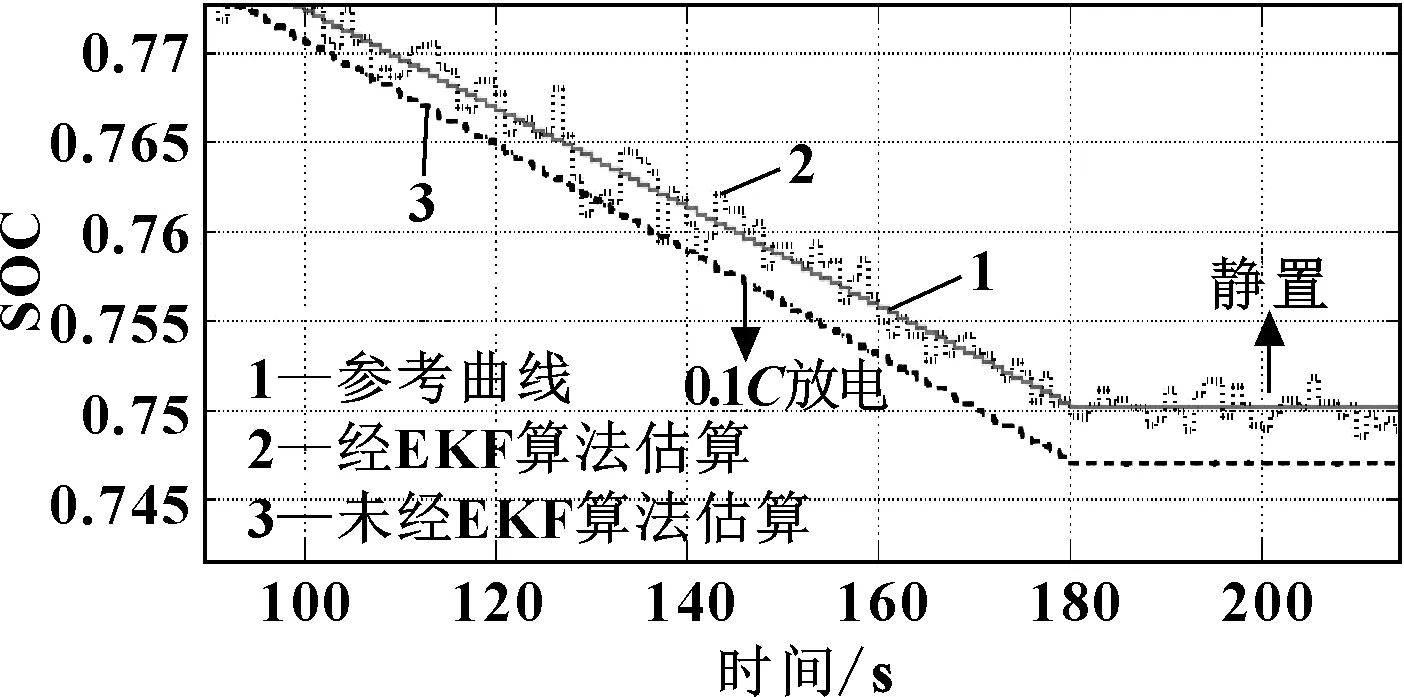
图8 25 ℃，1C充、放电倍率下SOC值局部放大图

曲线1为通过安时积分法得到的曲线。因为充、放电过程均为恒流充电、放电，因此，以这条曲线作为参考曲线，且赋予SOC初值SOC0为80%。曲线2是以EKF作为基础，结合复合电池模型，并经过容量修正、温度校正后得到的输出曲线。曲线3是以电池模型作为基础，以SOC值作为状态变量，未经EKF直接输出SOC估算曲线。

通过将不同充、放电倍率下的SOC输出值比较，不难发现，随着充、放电倍率增大，未经EKF的SOC估算输出曲线距参考曲线距离逐渐增大，误差逐渐增大。而无论是在1C倍率下，还是在3.4C倍率下，EKF输出曲线始终围绕参考曲线上下波动，随着均方误差逐渐减小，其值最终会收敛于参考曲线。且在这两种充、放电倍率下，EKF算法估算得到的SOC值比未经EKF、由电池模型直接得到的SOC估算值精度要高。体现了EKF算法的精确度高，稳定性好。

为验证温度对模型算法的影响，选择在3.4C充、放电倍率下，分别以-5、25 ℃进行充、放电，如图9所示。

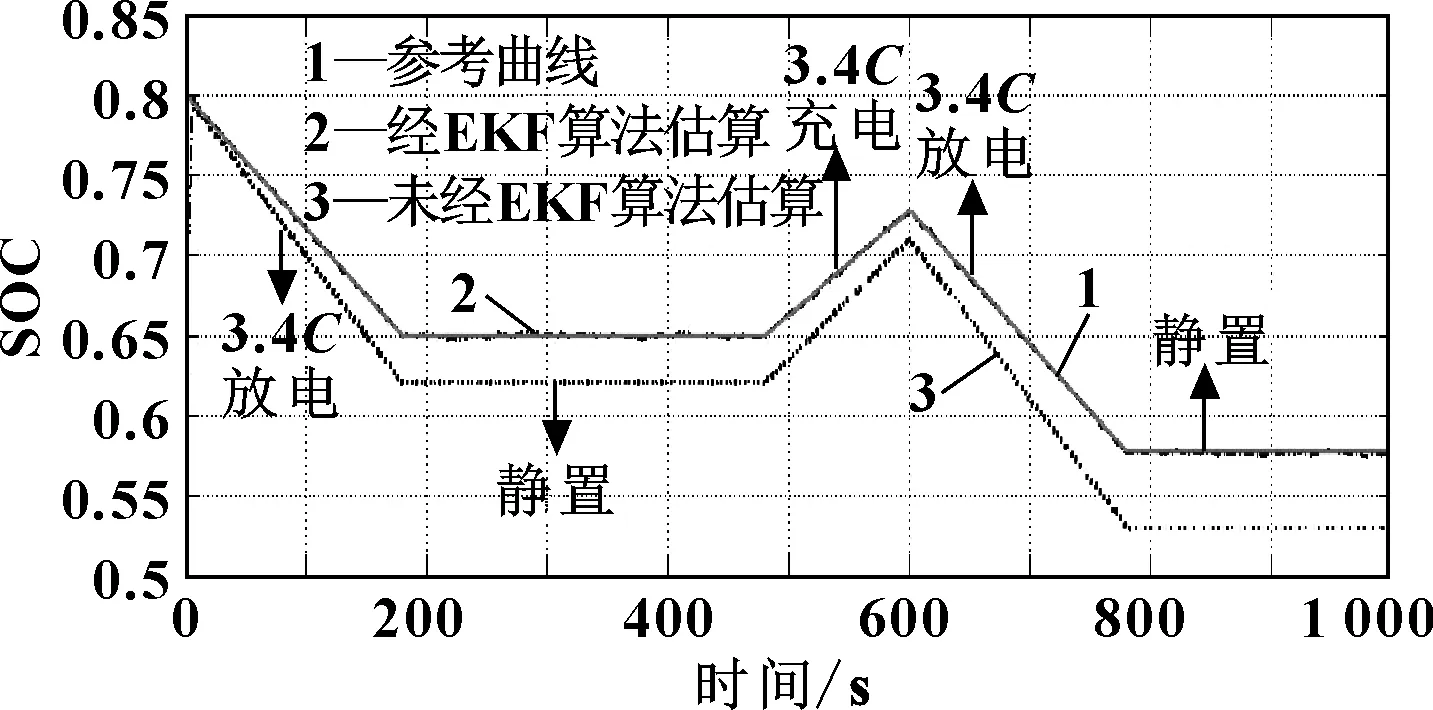
图9 -5 ℃，3.4C充、放电倍率下SOC值曲线图

通过图6和图9可以明显看出，温度对该算法影响很大，-5 ℃下未经EKF算法输出曲线与参考曲线误差较大，将近达到4%，而经EKF算法得到的SOC输出曲线在该环境下误差较小，经计算最大为0.5%，还存在围绕参考曲线来回波动的调节过程。说明EKF算法在极端环境中精确度较高，鲁棒性较好。

无论是以安时积分法为基础输出曲线，还是以电池模型为基础输出曲线，都需要赋予S0C初值SOC0，而EKF原理输出曲线的收敛性与初值SOC0无关。在EKF中，初值的准确与否只关系到算法的收敛时间，所赋初值和实际值之差的绝对值越大，收敛时间越长，反之越短。输出SOC曲线变化规律不会受到初值影响，属于EKF算法的优越性。

电动汽车在行驶过程中存在加速超车情况，此时电池需大倍率放电，因此以25 ℃，3.4C倍率放电为主要研究对象。如图6所示，所选择的数据范围为0.520 7～0.8。在开始放电阶段，卡尔曼滤波设置的初始值x0为0.630 5，与初值SOC0相差较大，根据卡尔曼滤波原理，为使均方误差最小，曲线迅速上升，在t=6 s时第一次与参考曲线相交，此时卡尔曼滤波算法预测结果几乎接近于SOC真实值。随后无论是在充、放电阶段，SOC预测曲线都在参考曲线附近上下摆动，在预测范围内多次穿越参考曲线并与之反复相交，说明模型精度高，反馈响应及时。但最终预测曲线并不会与参考曲线贴合，而是始终在其周围小幅震荡。原因如下：

(1)噪声矩阵对算法精度的影响。由于无法测量过程噪声和观测噪声真实值，将其假定为零，势必造成系统噪声在参数统计过程中存在误差，导致噪声参数设置不准确，反馈响应存在误差[8]。

(2)在充、放电过程中，由于电池极化效应影响，电池参数如电阻等会不断变化。在建模过程中，为保证算法的实用性和模型的难易度，舍弃了模型中极化效应修正部分，导致电池极化效应对模型响应产生影响。

而另外一条曲线虽能反映SOC变化趋势，但始终位于参考曲线下方，因为复合模型和系统原模型还存在偏差，在对等效模型进行更新时，由于迟滞效应导致复合模型和真值产生偏差，系统噪声为有色噪声，并不为零[9]。

图10为输出结果SOC绝对误差曲线图，曲线1为经EKF的绝对误差，计算开始后，真实初值SOC0和EKF中所赋初值存在偏差，根据卡尔曼滤波原理，均方误差逐渐减小，算法中SOC值向真值逐渐靠拢。误差曲线迅速向零靠近。SOC值在真值附近小幅震荡，因此误差值在零附近小幅震荡，且最大误差不超过0.5%，精度比较高。

曲线2是未经EKF滤波，经过复合模型后直接输出的SOC值的误差曲线，相对考虑容量校正、温度校正等的EKF误差曲线而言，误差相对较大，当t=600 s后，误差逐渐增大，整个过程都没有来回震荡的调节过程。EKF算法优越性展现无遗。

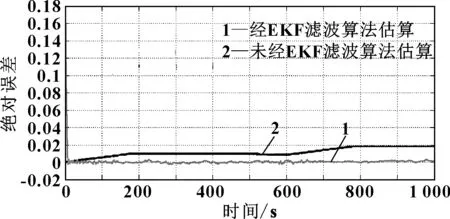
图10 25 ℃，3.4C倍率下SOC绝对误差曲线

4 结束语

本文作者以卡尔曼滤波为理论基础，结合复合电池模型，提出了基于扩展卡曼滤波的锂离子电池SOC估算方法，并添加了与电池表面温度有关的容量校正模型以及和库仑效率有关的电流效率模型，实现对SOC估算的校正。在MATLAB/Simulink中建立上述仿真模型，并对输出曲线进行分析。通过将经过EKF算法估算和未经EKF算法估算得到的SOC输出曲线进行比较，表明该算法估算精度较高，误差较小，且具有来回震荡的调节过程、抗干扰能力较强的优点。对于SOC估算的实际应用具有一定的参考价值。