利用最小冗余对称阵列的近场源定位算法
2018-12-07倪萌钰倪柳柳张佳佳
校 松,陈 辉,倪萌钰,倪柳柳,张佳佳
(空军预警学院 重点实验室,湖北 武汉 430019)
信号源定位问题是阵列信号处理中的一个重要的热点研究内容,广泛应用于雷达、声呐、通信等领域.在远场情况下入射到阵列的信号为平面波,所以只能对信号源进行测向,而不能定位.在国内外有大量的学者提出了众多的方法,例如多重信号分类(MUltiple SIgnal Classification, MUSIC)[1]算法、旋转不变子空间(Estimation of Signal Parameters via Rotational Invariance Techniques, ESPRIT)[2]算法等.当信号源位于近场条件时(即信源与阵列距离处于菲涅尔区域),平面波的假设不再成立,信号以球面波的形式传播,此时需要对信号的波达方向(Direction Of Arrival,DOA)和距离两个参数进行估计,从而实现近场源定位.
近10年来,国内外学者对于近场源定位问题进行了大量研究,各种方法相继提出.最初阶段主要集中在等距均匀阵列的研究上[3-8],但为了避免方位和距离模糊,均匀线阵的间距由半波长缩小至 1/4 波长.文献[3]的MUSIC算法将远场对角度一维估计的方法变成近场方位和距离二维估计方法,这类算法的精度高、性能稳健,但需要进行多维搜索,运算量非常大.为了克服这个缺点,人们利用等距均匀线阵的对称特点和高阶累积量来重构数据矩阵,从而将二维处理转化为一维的级联处理,减少了运算量.如文献[4]通过构造高阶累积量的ESPRIT算法来进行参数估计,文献[5-6]利用对称的阵列模型来进行DOA估计,这类算法的缺点是,重构后的虚拟阵列阵元数小于真实阵列,通常能估计的信源数不足阵元数目的一半.文献[7]构造高阶累积量矩阵进行参数估计,减小了孔径损失.文献[8]研究了阵元间距大于 1/4 波长时产生的模糊问题.这些算法都受到均匀阵列孔径的限制,估计精度和空间分辨率不高.
为了突破均匀阵列孔径的限制,很多学者针对非均匀线阵进行了一些研究[9-14].文献[9]采用对称稀疏阵列基于降秩的思想估计方位角,但这种方法会造成一半阵列孔径的损失.为了避免阵列孔径的损失,提高阵列的利用率,文献[10-11]分别采用互素阵列和对称嵌套阵列,构造高阶累积量矩阵对方位进行估计.文献[12]讨论了远场参数估计的稀疏嵌套阵列模型,大大提高了阵列自由度.文献[13]研究了近场中非均匀阵列的设计思路.笔者提出了基于最小冗余对称阵列[14]的协方差矩阵重构算法.该算法通过构造一个只与方位角有关的四阶累积量矩阵重构出阵列接收数据协方差矩阵,利用MUSIC算法进行信号DOA的估计;然后在估计出的角度的距离维上进行搜索,得到距离参数,从而实现定位.该算法既扩展了阵列的孔径,提高了估计性能和空间分辨率,又提高了阵列自由度,可以估计更多的信源数目,且只须进行一维搜索,无需进行参数配对.
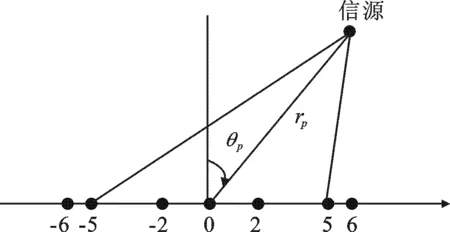
图1 对称最小冗余阵列模型
1 近场信号模型
文中采用的阵列模型是最小冗余对称阵列,阵元数为2M+1,阵元位置以d为单位,阵元的坐标为l-Md,l-M+1d,…,lMd.如图1所示,以M=3 为例,即是一个7元阵构成的最小冗余对称阵列.
假设有P个窄带近场信号,以中心阵元0为参考阵元,则阵元m接收到的信号可表示为
(1)
其中,sp(t)为阵元接收到的第p个信号源,nm(t)是阵元m接收到的噪声,τpm为第p个信源在阵元m和阵元0之间的时延差,其可表示为
(2)
其中,λ为信源的波长,θp为第p个信源的入射角,rp表示第p个信源与参考阵元之间的距离.式(2)由菲涅尔近似可表示为
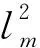
(3)
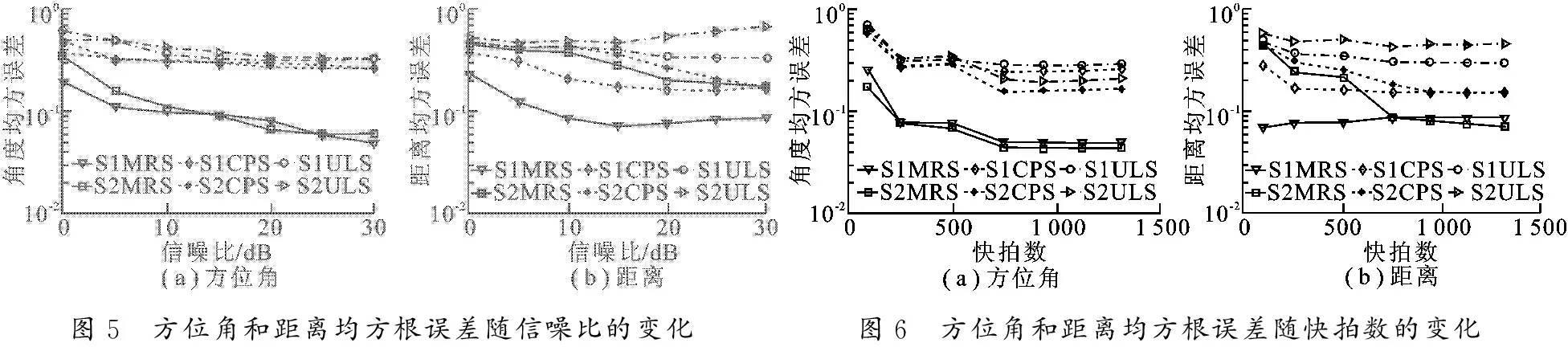
其中,μp=(-2πd/λ) sinθp,φp=[πd2/(λrp)] cos2θp,rp满足 0.62(D3/λ)1/2 (4) 则阵列接收信号用矩阵形式表示为 不失一般性,进行如下假设: (1) 各信源为零均值、独立的非高斯窄带平稳随机过程,具有非零峰度. (2) 阵元噪声为零均值的高斯噪声,各阵元噪声独立,且与信源不相关. (3)d=λ/4,λ为信源波长,信源个数P≤2M. 根据对称阵列和高阶累积量的性质,构建只与信源方位角有关的四阶累积量: (11) 其中,m,n∈[0,M],xm为第m个阵元的接收数据.由高阶累积量的性质可以简单推导得到 (14) z=[Rx(-6),Rx(-5),…,Rx(0),…,Rx(5),Rx(6)]T. (15) 根据列向量z构造7×7维Toeplitz矩阵Z,可表示为 (16) 在高斯噪声的假设下,矩阵Z为重构的阵列接收数据的协方差矩阵,其可表示为 根据式(17)~式(20)得到,矩阵Z等效于远场虚拟阵元数为7的等距均匀线阵(间距为λ/2) 所接收到的阵列协方差矩阵,对其进行特征分解得到: (21) 其中,US是由P个大特征值对应的特征矢量张成的信号子空间,ΣS是P个大特征值组成的对角矩阵,UN是由 7-P个小特征值对应的特征矢量张成的噪声子空间,ΣN是 7-P个小特征值组成的对角矩阵.根据MUSIC算法的谱可以得到信源方位角的估计值: (22) 图2 实际阵列与虚拟阵列 图2为实际阵列与虚拟均匀线阵阵列结构图,其中“●”代表实际对称最优最小冗余阵列,“■”为等效的虚拟均匀线阵. 由上述过程可知,利用以d=λ/4为单位的最小冗余对称阵列模型来构建高阶累积量矩阵,其可以等效为阵元数目更多的间距为半波长的虚拟等距均匀线阵.该阵列模型相比于同阵元数的均匀线阵,扩展了阵列的孔径,增加了阵列的自由度,可以估计更多的信源角度,且不会产生模糊. R=E[X(t)X(t)H] , (23) (24) 上述估计方法只需对谱函数进行P次一维搜索就得到信源距离的估计值,避免二维搜索,无须参数配对,减少了计算量,仅需P+1 次搜索就可得到信源的角度与距离参数,实现定位. 由文献[14]可知,最优的最小冗余阵列其阵元数为4,即最优的最小冗余对称阵列阵元数为7,当阵元数大于7时,则采用非最优最小冗余阵列模型进行估计(除了零之外,其余位置也可以有冗余性).表1给出了部分不同阵元数的非最优最小冗余对称阵列所能等效均匀线阵的虚拟阵元数目和孔径. 表1 不同阵元数的非最优最小冗余对称阵列 可以看出,当实际冗余对称阵列模型阵元数大于7时,其等效的均匀线阵虚拟阵元数大于实际阵元数,并且随着实际阵元数的增大,所等效的数目也越来越多,阵列自由度也随之增大.由于在距离估计中利用实际阵列接收数据协方差矩阵,因此当实际阵元数为Q(Q≥7) 时,文中最小冗余对称协方差矩阵重构(Minimum Redundant Symmetric covariance matrix reconstruction,MRS)算法可估计Q-1 个信源,而文献[5,9]算法只能达到MRS算法估计信源数的一半. 当阵元数相同时,以实际阵元数11为例,表2给出了MRS算法与等距均匀阵列(Uniform Linear Symmetric,ULS)以及文献[10]基于互素阵列(Co-Prime Symmetric,CPS)算法的阵列孔径比较.可以看到,MRS算法相比ULS算法和CPS算法,可等效更多的虚拟阵元数,扩展了阵列孔径,并且随着阵元数的不断增大,获得的孔径越来越大. 表2 3种阵列孔径比较 3种算法的计算量对比,差距主要来自于构造的高阶累积量矩阵,当阵元数为Q时,MRS算法与ULS算法同样都是构造一个[(Q+1)/2]×[(Q+1)/2]维的累积量矩阵,CPS算法构造一个 [(Q+1)(Q+5)/ 8-1]×1 维向量.由此可见,MRS算法与ULS算法计算量相当,CPS算法计算量较小,但其孔径和估计精度不如MRS算法的. 在仿真试验中,考虑如图1所示的7阵元最优最小冗余对称阵列以及表1中11阵元的非最优最小冗余对称阵列,其位置矢量Y= (-13,-10,-6,-2,-1,0,1,2,6,10,13)d.为了验证算法的性能,在相同阵元数情况下,将MRS算法与ULS算法以及CPS算法进行比较.在算法统计特性比较中,采用均方根误差(Root Mean Square Error,RMSE)作为评价指标,即 (25) 实验1 角度和距离谱图.两个相互独立等功率的近场窄带信号分别入射到图1最优最小冗余对称阵列和与其阵元数相同的等距均匀线阵(阵元间距λ/4) 上.信源位置参数分别为(-10°,3.5λ)和(8°,3.5λ),快拍数设为500,信噪比为 10 dB,仿真结果如图3所示.图3中S1代表第1个信源,S2代表第2个信源. 从图3中可以看出,两种阵列模型都可以在DOA估计中形成谱峰,并且没有伪峰.但MRS算法谱峰更加尖锐,估计更为精确,更加接近真实角度.同时在距离估计中,MRS算法形成的谱峰远远好于ULS算法的.这说明,在阵元数较少的情况下,MRS算法相比于ULS算法,扩展了阵列孔径,估计性能更好. 实验2 多阵元DOA谱图及空间分辨率.两个相互独立等功率的近场窄带信号,分别入射到11阵元的非最优最小冗余对称阵列和与其阵元数相同的等距均匀线阵以及文献[10]互素阵列上.信源位置参数分别为(5°,10λ)和(15°,20λ),快拍数设为500,信噪比为 10 dB,分别画出其DOA谱图.缩小角度间隔,当信源位置参数变为(7°,10λ)和(9.5°,20λ)时,画出DOA谱图,结果如图4所示. 从图4可以看出,在角度间隔比较大时,MRS算法和CPS算法都可以在真实角度处形成比较尖锐的谱峰,可以分辨出两个信号方向,而ULS算法则出现伪峰,无法分辨出两个信号角度.而当角度非常接近时,MRS算法所形成的谱峰更接近真实角度,而CPS算法偏离了真实角度.这说明MRS算法相比于CPS算法有着更好的角度分辨率. 实验3 算法统计特性仿真.两个信源位置参数同实验2的第1次仿真参数,仿真结果采用200次蒙特卡罗统计实验.图5给出了不同信噪比下3种算法方位和距离估计的均方根误差图,快拍数设为500.由于3种算法均采用高阶累积量,算法精度受快拍数影响比较大.图6给出了不同快拍数下3种算法的DOA和距离估计的均方根误差图,信噪比为 10 dB. 从图5可以看出,3种算法的均方根误差均随着信噪比的增大而减小,MRS算法的估计性能明显好于CPS算法以及ULS算法的,这是因为在同阵元数的情况下,MRS算法基于对称最小冗余阵列模型,利用四阶累积量重构阵列接收数据协方差矩阵,有着更大的阵列孔径.而在距离估计中,3种算法对信源1的距离估计精度明显大于信源2的,这表明信源距离越近,距离的估计就更加准确,定位精度更高,这与文献[4]中的理论分析一致.从图6可以看出,3种算法的均方根误差均随着快拍数的增大而减小,而MRS算法的估计精度明显高于CPS算法以及ULS算法的. 文中提出了一种基于最小冗余对称阵列的近场源角度和距离估计的协方差矩阵重构算法.该算法首先构造一个仅与信号角度有关的四阶累积量矩阵,从而重构出阵列接收数据协方差矩阵,利用MUSIC算法进行信号DOA的估计,然后在估计出的角度方向的距离维上进行搜索,估计出信号的距离.该算法克服了传统的基于均匀线阵方法造成孔径和阵元数损失,阵列自由度不足阵元数一半的缺点,扩展了阵列的孔径,拥有更好的估计精度和分辨概率,并且增加了阵列的自由度,可估计出更多的信源数目.2 最小冗余对称阵列的定位算法
2.1 信号DOA估计
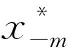
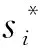
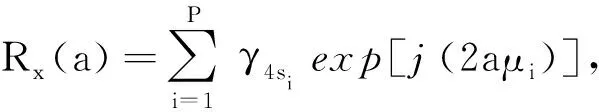
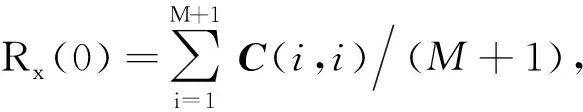

2.2 信号距离估计
2.3 虚拟阵元数分析


3 计算机仿真
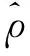

4 结 束 语
