一种动态分群带熵权的粒子群优化方法
2018-12-07刘道华胡秀云赵岩松崔玉爽
刘道华,胡秀云,赵岩松,崔玉爽
(1. 信阳师范学院 计算机与信息技术学院,河南 信阳 464000;2. 信阳师范学院 河南省教育大数据分析与应用重点实验室,河南 信阳 464000)
粒子群优化算法(Particle Swarm Optimization,PSO)是一种群体智能的随机优化算法,由于其具有控制参数少、收敛速度快和寻优效果好等优点,广泛应用于复杂多峰优化问题的求解.为了增强粒子群算法的全局搜索能力,许多学者采用了各种改进策略以提高粒子群优化算法的求解性能.在众多的改进算法中,基本上均是从参数优化、解的邻域选择、种群划分以及算法混合上进行改进.在参数优化改进上,如文献[1]发现当惯性权重随迭代次数线性递减时算法寻优效果较好.文献[2]设计了一种基于离散度大小的动态调整粒子群参数的优化方法.在解的邻域选择上,文献[3]利用个体粒子间“充分信任”的信息,提出了一种粒子群优化算法邻域结构的选择方法.文献[4]利用粒子的衰退机理,提出了一种动态调整全局最优型邻域结构的方法,以增强粒子寻优时最优解的多样性.在种群划分上,文献[5]采用主-从群混合进化的粒子群算法优化规则参数,建立了一种基于双启动标准的限制供水解析规则,以此提高算法的求解精度和收敛速度.文献[6]提出了一种基于分类的自适应粒子群优化算法.在算法混合上,文献[7]针对目前粒子群优化算法在多零点低旁瓣约束的阵列天线方向图综合中早熟收敛、易陷入局部极值的问题,融合混沌优化算法和粒子群优化算法的优点,提出了一种新的混合优化算法.文献[8]提出了一种混合小生境粒子群优化算法,以求解复杂多峰优化问题.总之,这些改进策略均提高了粒子群算法的求解性能.但既采用分群划分的改进策略,同时又使用参数调整的策略,这样的文献还很少见.基于此,笔者将粒子群依据k的均值聚类划分成若干个子群,同时以子群为中心,更改子群算法的参数,将子群粒子优化过程中的熵信息融入到子群惯性权重参数ω的调整上,通过经典的Benchmark典型测试函数进行验证,并同其他优化方法进行求解对比得出,这种动态分群带熵权的粒子群优化方法具有收敛速度快、解的精度高,尤其在对复杂的多峰病态函数求解时,既能获得函数的所有峰值解,又能提高解的精度.
1 粒子群算法动态分群及带熵权策略
1.1 粒子群算法动态分群策略
传统的粒子群算法基本上均为一个群体,这种方法用于求解复杂多峰函数时,很难找全所有峰值解,尤其对于复杂局部近似峰值解时,该方法更难找全局部峰值解.为了获得复杂多峰函数所有峰值解以及所有局部峰值解,采用多子群且先粗搜索后精搜索的方式进行求解.在粗搜索的过程中,先将初始化后的随机粒子或是优化迭代一步后的粒子采用k均值聚类的方式构建k个子群体,每个子群体依据自身子种群对原问题进行优化迭代的每一次,均将执行一次k均值聚类重新分群,从而实现粒子群动态分群策略.
1.2 粒子群算法带熵权策略
在传统的PSO算法中,设搜索空间的维数为D,粒子群个体规模为s,则第i个粒子的当前位置状态xi= (x1,x2,…,xD)T,当前速度vi= (v1,v2,…,vD)T,当前搜索到最优位置pi= (pi,1,pi,2,…,pi,D)T,i=1,2,…,s.设整个种群搜索到最优位置时对应粒子下标为g,则PSO中各粒子的速度位置更新方程为
其中,t为当前迭代次数,t=1,2,…,maxgen;d表示维度,d=1,2,…,D;c1和c2分别为个体认知因子和社会认知因子,但在一般情况下,c1=c2= 2;r1和r2为随机数,独立服从区间(0,1)上均匀分布;ω为惯性权重[9].
从式(1)和式(2)可以看出,传统粒子群算法的关键参数分别为惯性权重参数ω、加速因子参数c1及c2.许多学者都提出ω的值应该在算法搜索迭代过程中线性下降,ω可表示为
ω=ωmax-(ωmax-ωmin)g/G,
(3)
其中,g是算法的当前迭代次数,G是最大迭代次数,ωmax和ωmin一般设为0.9和0.4.
这种传统的惯性权重参数调整方法不能很好地获得其他粒子熵信息.基于此,在任一子群进行粗搜索时就充分利用其他子群的熵信息,因此,对于式(1)中的ω将采用如下操作方式获得.
假定通过k均方聚类获得k个聚类中心,则设子群数为k个,当然每个子群所包含的粒子数可能不相等.在每个子群经过m次迭代后,每个子群获得的优化解设为Aj,其中j∈ (1,2,…,m),则k个子群经过m次迭代后所构建的最优解矩阵D为
(4)
全局最优解D归一化后,得
(5)
每个子群在迭代搜索m次时全局解Aj的信息熵为
(6)
(7)
由于式(1)中的r1和r2为随机数,且独立服从区间(0,1)上均匀分布,则该参数不能充分利用本群内其他粒子的信息熵.基于此,将参数r2附加上自身群内不同粒子间迭代搜索的熵信息,此时自身群n个粒子经过m次迭代时获得的优化解设为Aj,其中j∈ (1,2,…,m),则n个粒子经过m次迭代后所构建的最优解矩阵D为
(8)
同样,本群内新的信息熵权为
(9)
同样,采用式(5)及式(6)计算Ej所用的Aij将依据式(8)计算得出.
相应地,将式(1)更改为
vi,d(t+1)=ω′vi,d(t)+c1r[pi,d(t)-xi,d(t)]+c2[ω″pg,d(t)-xi,d(t)] .
(10)
在精搜索过程中,不存在其他子群的熵信息,仍采用k个子群构建k个粒子,每个粒子的初始位置以当前群获得的最优解为初始设置,进行PSO精搜索.在精搜索过程中,依据每一子群搜索到最优解时那一粒子的最终信息构成新粒子群的初始信息,即此时群体有k个粒子.式(10)中不存在其他子群的熵信息,此时的ω′将以式(1)中的ω代替,而Aj为k个粒子经过m次迭代时的最优值.则该群内全局优化解将附加的信息熵权为
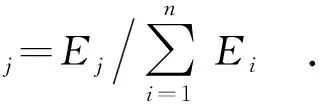
(11)
同样,此时采用式(5)及式(6)计算Ej所用的Aij将依据式(8)计算得出.
相应地,将式(1)更改为
vi,d(t+1)=ωvi,d(t)+c1r[pi,d(t)-xi,d(t)]+c2[ω‴pg,d(t)-xi,d(t)] .
(12)
2 动态分群带熵权的粒子群优化方法
动态分群带熵权的粒子群优化方法先进行粗搜索,以获得复杂多峰最优解或近似最优解,并将该最优解作为精搜索的初始信息.该方法粗搜索的具体步骤如下:
步骤1 初始化.依据被优化多峰函数的难易程度选择初始群体的规模s,最大迭代次数maxgen,迭代次数计数器t为0、ωmax和ωmin,初始化粒子群,即随机设定各粒子的初始位置x和初始速度v.
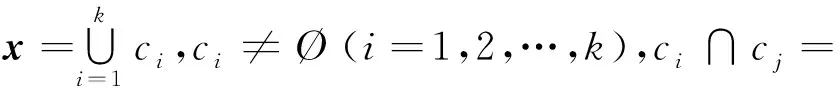
步骤3 计算所有子群每一个粒子的适应度值.
步骤4 比较所有子群每个粒子的适应度值和它自身经历过的最好位置pi,d的适应度值,如果优于先前最优值,则用此时适应度值替换原pi,d值.
步骤5 寻找当前所有群所有粒子的最优位置适应度值pd.
步骤6 比较所有子群每个粒子的适应度值和该子群体经历过的最好位置pg,d的适应度值,如果优于先前最优值pd,则用此时适应度值替换原pg,d值.
步骤7 分别计算式(2),式(4)~式(10),调整各子群各粒子的速度及位置.
步骤8 迭代计数器t=t+1.
步骤9 判断是否达到最大迭代次数,如满足,则退出循环;否则,转步骤2.
该方法精搜索的具体步骤如下:
步骤1 将粗搜索各子群获得最优位置及速度的粒子作为精搜索粒子群的初始条件(粒子个数与原子群个数相同),重新设置最大迭代次数,迭代次数计数器t=0.
步骤2 计算各个粒子的适应度值.
步骤3 比较每一个粒子适应度值和它自身经历过的最好位置pi,d的适应度值,如果优于先前最优值,则用此时适应度值替换原pi,d值.
步骤4 比较每一个粒子适应度值和该群体经历过的最好位置pg,d的适应度值,如果优于先前最优值,则用此时适应度值替换原pg,d值.
步骤5 分别计算式(2)~式(6),式(11)~式(12),调整各粒子的速度及位置.
步骤6 迭代计数器t=t+1.
步骤7 判断是否达到最大迭代次数,如满足,则退出循环;否则,转步骤2.
3 实例及分析
为了验证该优化方法求解复杂函数的有效性,以如下4个代表性的Benchmark测试函数为例:

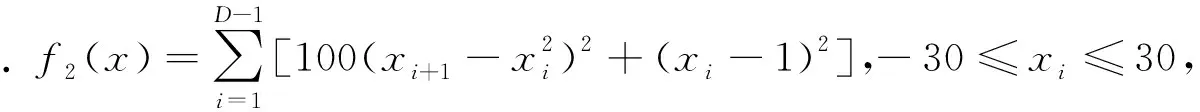


4个函数在三维坐标下的图像如图1所示.

图1 4个测试函数的函数图像
基于上述4个代表性的不同种类型的测试函数,用文中方法与传统的PSO方法、文献[9]所提多策略粒子群优化(Multi-strategy Particle Swarm Optimization,MPSO)方法进行算法性能比较.
在实验过程中,采用Intel(R) Core(TM) i3-2120 CPU,@ 3.30 GHz,并在MATLAB R2008a编程环境下进行求解验证.每个测试函数维数D固定设置为10,每个函数采用每种方法独立运行50次,统计每个函数的最优值、平均值、标准差以及平均迭代数(若没找到最优解则将其视为最大迭代次数).对于传统的PSO方法,其算法参数设置: 个体规模s= 30,最大迭代数G= 1 000,个体认知因子和社会认知因子c1=c2=2,惯性权重ωmax和ωmin分别为0.9和0.4.对于MPSO方法,其算法参数设置:维数D= 30,种群大小ps= 20,最大速度vmax= 0.1xmax,加速系数c1=c2=2.对于文中方法,其算法参数设置: 个体规模s= 100,最大迭代数 maxgen= 1 000,个体认知因子和社会认知因子c1=c2=2,式(12)中惯性权重ωmax和ωmin分别为0.9和0.4.实验结果如表1所示.
从表1中数据对比可知,文中方法的平均迭代数远少于传统PSO方法和MPSO方法的,这充分体现文中方法具有较高的优化效率.而文中方法的最优值、平均值以及标准差也优于其他两种方法对应的指标,表明文中方法具有较强的求解稳定性.由于4个函数的理论值均为零,在实验中,尤其对于复杂多峰函数f3及f4具有大量局部极值点,由于文中方法利用了其他熵权信息,而且在精搜索过程中,许多局部极值点在粗搜索过程中就事先找到,从而提高了整个算法的搜索效率.总之,文中方法是一种综合性能较好的粒子群优化算法.

图2~图5给出了4个函数3种方法的优化曲线对比图.从图2~图5中可以看出,在对4个典型函数的优化求解过程中,只有对于f3函数,文中方法优化迭代次数略高于其他两种方法,但获得解的精度远高于其余两种方法.对于f1、f2以及f4函数,文中方法获得优化解的精度均高于其他两种方法的,而且在获得所求函数的最优解时,所用优化迭代次数远少于其他两种方法.同时算法从一开始就能及早地达到问题的最优解,而且达到最优解后,算法一直处于收敛状态,不存在振荡现象,体现出该方法具有稳定的求解性能.

4 结 束 语
采用k均值聚类方法获得子群的分类个数,并且在所有粒子优化迭代每一次后重新执行k均值聚类分群,从而实现动态分群策略.充分利用其他子群的熵信息,以构建不同子群的熵权,从而提高了整个算法的收敛效率.利用子群粗搜索获得的信息作为精搜索粒子群初始信息,从而充分利用了先前子群获得的最优解信息,使得该方法极易获得复杂多峰函数的局部极值点;同时,这种方法也极易获得复杂多峰函数的所有全局不同最优解.这种动态分群带熵权策略也为其他群智能方法的改进提供了很好的借鉴.
