基于IC卡数据的公交下车站点区间不确定性客流推导方法

柳伍生，周向栋，匡凯



基于IC卡数据的公交下车站点区间不确定性客流推导方法

柳伍生，周向栋，匡凯

(长沙理工大学 交通运输工程学院，湖南 长沙 410004)

在交通大数据背景下，针对现有公交客流推导研究中站点客流皆为固定单一值与实际波动区间值不符的问题，利用区间不确定性理论，以及公交IC卡数据与GPS数据相结合，得到上车站点的公交区间客流。对公交刷卡行为进行分析，考虑乘客个体出行特征和乘客出行距离于站点吸引权重中，得到下车站点客流推导概率模型，结合区间不确定性理论，得到下车站点客流区间值。以深圳市的21路公交IC卡数据和GPS数据为例进行实例分析。通过对推导结果的合理性分析，表明得到的公交区间不确定性客流，更符合实际，算法流程清晰，具有更好的可靠性。

公交客流OD；区间不确定性理论；IC卡数据；GPS数据；下车站点

传统的公交客流往往依靠人工调查，数据采集主要为人工调查方法。传统方法往往通过人工问卷调查法获取公交出行OD，需要耗费大量的人力、物力，且样本数量少、精度不高。近年来，以公交IC卡为主的数据分析方法，数据丰富全面有效，费用较低，是现在公交客流OD研究的主流方法[1−4]。国外对结合大数据的公交客流OD研究较早，也相对成熟。Barry等[5]依托大数据分析实现了对纽约市的公交客流OD推导。ZHAO等[6]针对地铁−地铁，地铁−公交的2类出行链做了公交客流推导，CUI[2]对于不同规模的公交客流研究了相应的推导方法。Pelletier等[7−12]采用公交智能卡对出行目的、出行链等进行分析。国内对于公交客流OD的推导研究较晚。胡郁葱等[13]通过IC卡数据挖掘技术获取了公交OD矩阵。陈峥嵘[14]将智能公交数据处理方法应用于公交客流OD研究。胡继华等[15]提出结合出行链的IC卡公交客流研究方法。国内学者研究主要集中于IC卡数据的下车站点的客流推导确定值问题[16−20]。结合大数据，国内外对于区间不确定性分析研究较少。全维杰等[21−22]分别采用双层规划模型及高维代理模型对区间不确定性问题进行分析。Averbakh等[23−25]分别研究了带区间的后悔网络优化问题以及离散区间的优化问题。实际上，复杂的公共交通环境以及乘客的个体随机出行特征，使得上下车客流往往在一个区间范围内波动，但过去的方法往往得到的是一确定值。给定一个区间客流值给决策者提供更好的支撑。本研究通过区间不确定性理论与交通大数据相结合，以出行链的思想，对一天刷卡次数行为进行分析，结合乘客出行站数和乘客个体出行特征，以公交IC卡数据和GPS数据为基础，对公交客流区间OD推导方法进行系统研究，并以深圳市公交数据为实例进行分析研究。

1 公交数据处理与上车站点的确定

本研究数据来源于深圳市公交IC卡和公交GPS数据，公交线路及站点基础数据，选取深圳市常规公交IC卡系统数据卡编号，刷卡时间，车辆编号，线路编号4个数据类型，GPS系统数据中终端ID(车辆编号)，GPS系统时间，接受时间，经纬度4个数据类型，线路及站点基础数据中线路名称，线路车辆编号、站点名称，站点经纬度4个数据类型，车辆编号与车牌号之间有种对应关系，终端ID与车牌号之间有种对应关系。筛选得到的公交基础数据见表1，所得公交融合数据见表2。

表1 公交基础数据

表2 公交融合数据

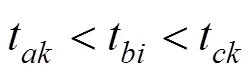
其中：t为车辆到站时间；t为车辆离站时间。

2 区间不确定性理论

在实际复杂的公共交通环境下，公交客流OD时刻在变化，存在或多或少的不确定性因素。依托交通大数据，通过对海量公交客流数据进行分析，可得公交客流OD区间集合。传统公交客流OD推导方法未考虑区间不确定性因素，使用区间不确定理论，可减少简化和假设，使得模型更真实更符合实际。

区间不确定性理论在数学上叫做区间数优化方法[20−22]。通过一个参数取值的波动区间集合，对该区间集合进行优化即区间数优化。区间数优化方法一般以概率大小来确定不确定约束及控制的满意程度，不确定性目标函数的性能由多个约束保证，具有更好的灵活性和柔性。区间数优化方法分为3类：一为基于区间数序关系的线性区间数优化，二为基于最大最小后悔准则的线性区间数优化，三为非线性区间数优化。

3 下车站点区间客流推导

3.1 公交刷卡行为分析

结合现实生活中存在和人共乘，一卡多刷的现象，提出和人共乘行为的假设：如果同一卡号的连续2次以上的刷卡记录的时间间隔小于对应站点间的行程时间，则后几条刷卡记录判定为和人共乘记录。假设和人共乘人员出行路径一致，即两者下车站点一致(假设1)。对刷卡数据进一步整理，对代刷次数合并整理，以下刷卡次数为已合并代刷的刷卡次数。

实际生活中公交乘客存在一天多次的刷卡行为，本研究对一天刷卡次数1至4次的行为进行了分析，对于刷卡次数超过4次以上的少数情况忽略不计，不予考虑，本研究选取一天刷卡次数4次以下数据为研究数据对象。依据出行特征将刷卡数据进行分类分析，从而对下车站点进行分类推导，分类方法见表3。部分一天多次的刷卡记录可依据表1的上下车站点推导依据直接推导得出。

表3 IC卡上下车站点推导依据

结合刷卡行为分析，结合实际运营中，公交乘客于同一站点间换乘，提出换乘假设：乘客下次刷卡站点位于当次乘客刷卡上车站点的下游站点(当次乘客线路行驶方向向下)且时间间隔为当次乘车所用时间波动区间内，则乘客当次乘车的下车站点为下次乘车上车站点(假设2)。

3.2 下车站点客流推导模型

现有公交IC卡信息中无乘客下车信息，依本研究上车站点确定方法，可得乘客上车站点具体情况，下车站点可通过挖掘乘客出行规律和站点的客流特征来进行推导，从而预测一天的下车站点客流。乘客出行站数分布具有一定的统计分布规律，本研究采用泊松分布。

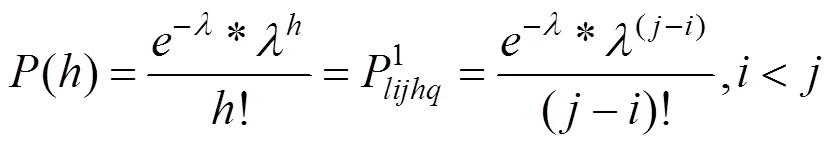
个体乘客的出行概率，在任意站点上车的特定乘客，在线路l下游任意站点下车，定义 如下：

1) 下游站点集合：运行方向下线路l在上车站点的下方所有站点集合。

2) 高频站点集合F：下游站点集合中，乘客上下车频次高的站点。由于每个乘客的高频站点各不相同，F为乘客前天上车站点记录的集合与E的交集。F中的站点需满足如下条件，乘客在该站点的前天上车次数高于数值。的取值由前天的时间跨度所决定，从而得到高频站点集合F。

3) 换乘枢纽站点集合G：乘客下次乘车的上车站点与的交集。

若G非空，则站点对特定乘客的站点吸引权为：

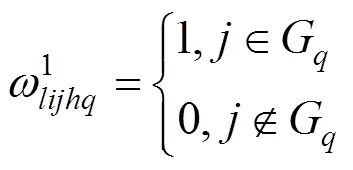
若G为空，F非空，则站点吸引权重为

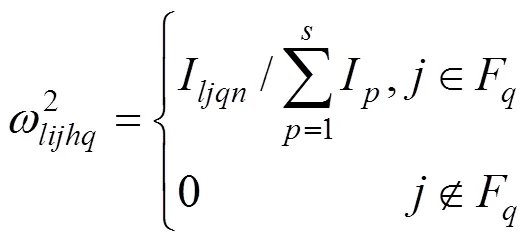
其中：I为在线路l上，特定乘客在前天在站点的上车次数；为高频站点集合包含的站点 个数。

若G为空，F为空，则站点吸引权重为

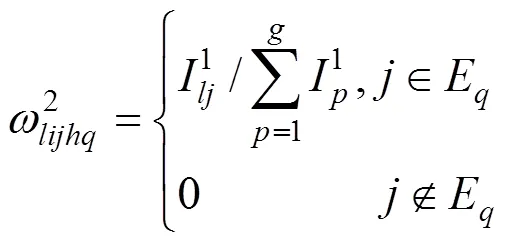
综上，考虑乘客个体出行特征情况，线路l上在站点上车的特定乘客，经过个站点在站点下车的概率为

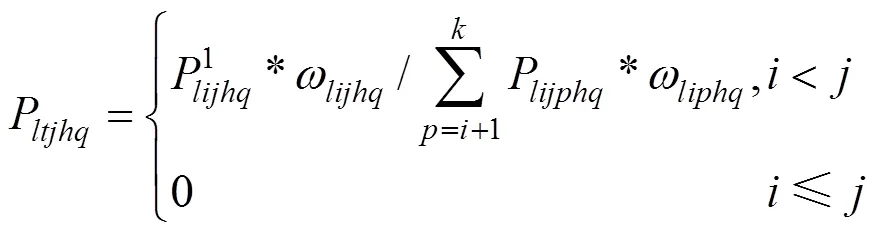
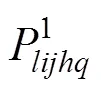
3.3 下车客流区间推导

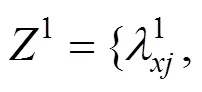
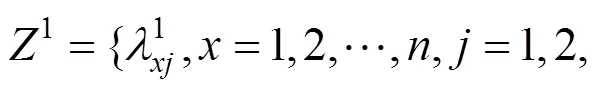
4 实例分析

依据本研究下车站点客流推导流程法则，进行下车站点推导，高频站点集的频次约束不低于3次，乘客近期出行的历史数据为2015−11−10~2016− 01−10的深圳市21路刷卡数据，判断出下车站点的数据总数共61 610条，其部分计算结果和下车站点客流区间如表4和图1所示。2016−01−13对深圳市21路进行区间抽样调查得到扩样系数表见表5，全天各站点下车人数调查统计见表6，各站点全天调查下车人数与预测下车站点客流区间进行有效性判别，结果显示，该天客流均在预测客流区间范围内，见表6，得调查客流在预测区间范围内占比例95.55%，准确度高，具有很高的实际调度参考价值。

表4 算法部分计算结果

图1 下车客流区间分布图(单向)

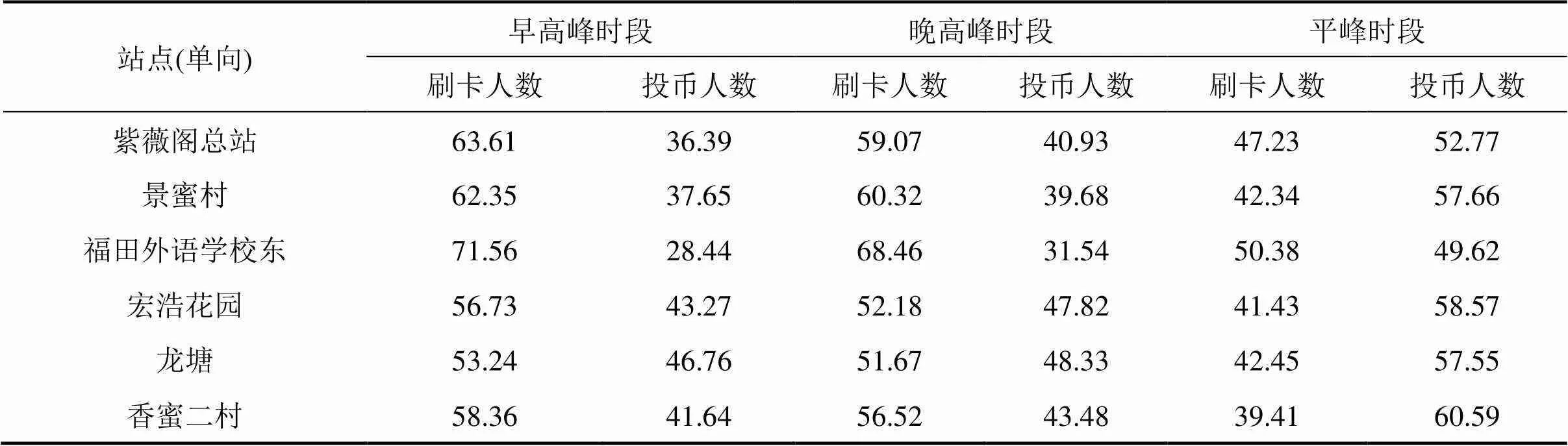
表5 部分扩样系数

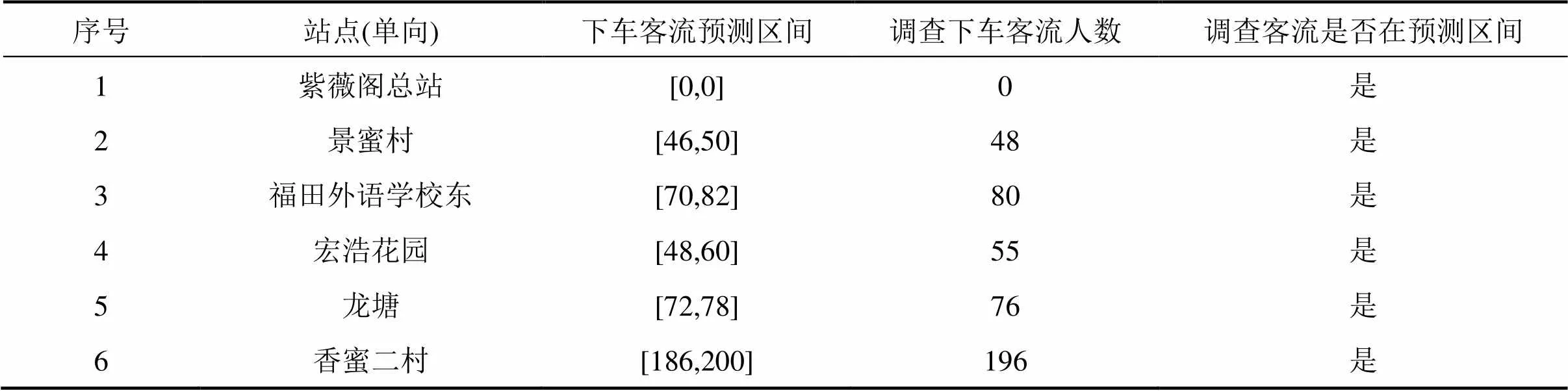
表6 部分下车客流区间检验

5 结论

1) 分析公交乘客刷卡行为特性，结合区间不确定性理论，考虑乘客个体出行特征和乘客出行距离于站点吸引权重计算模型，得到单条线路乘客上车客流区间值，更符合实际分布。

2) 对于乘客上车客流区间值分布研究，本研究可做到每天每个时段的精确分布；对于乘客下车客流区间值分布研究，本文研究每天的客流区间分布，对于每个时段的客流区间分布将是下一步研究重点，同时将通过可靠的居民出行OD数据结合交通大数据，得到公交出行交通出行区间OD。

[1] Bagchi M, White P R. The potential of public transport smart card data[J]. Transport Policy, 2005, 12(5): 464−474.

[2] CUI A. Bus passenger origin-destination matrix estimation using automated data collection system[D]. Boston: Massachusetts Institute of Technology, 2006.

[3] 杨万波, 王昊, 叶晓飞, 等. 基于GPS和IC卡数据的公交出行OD推算方法[J]. 重庆交通大学学报(自然科学版), 2015, 34(4): 117−121. YANG Wanbo, WANG Hao, YE Xiaofei, et al. OD matrix inference for urban public transportation trip based on GPS and IC card data[J]. Journal of Chongqing Jiaotong University (Natural Science), 2015, 33(4): 117−121.

[4] 陆百川, 邓捷, 马庆禄, 等. 基于IC卡和RBF神经网络的短时公交客流量预测[J]. 重庆交通大学学报(自然科学版), 2015, 34(6): 106−110. LU Baichuan, DENG Jie, MA Qinlu, et al. A short-term public transit volume forecasting model based on IC card and RBF neural network[J]. Journal of Chongqing Jiaotong University (Natural Science), 2015, 34(6): 106− 110.

[5] Barry J, Newhouser R, Rahbee A, et al. Origin and destination estimation in New York City with automated fare system data[J]. Transportation Research Record, 2002, 18(17): 183−187.

[6] ZHAO J H. The planning and analysis implications of automated data collection systems: rail transit OD matrix inference and path choice modeling examples[D]. Cambridge: Massachusetts Institute of Technology, 2004.

[7] Pelletier M P, Trépanier M, Morency C. Smart card data use in public transit: A literature review[J]. Transportation Research Part C, 2011, 19(4): 557−568.

[8] Markus Hofmalill, Margaret O’Mahony. Transfer. Journey identification and analyses from electronic fare collection data[C]// Proceedings of 8th International IEEE Conference on Intelligent Transportation Systems, Vienna, Austria, 2005.

[9] ZHAO Jinhua. The planning and analysis implications of automated data collection systems: Rail transit OD matrix inference and path choice modeling examples[D]. Massaehusetts Institute of Teehnology, 2004.

[10] Sang G L, Hickman M. Trip purpose inference using automated fare collection date[J]. Public Transport, 2014, 6(2): 1−20.

[11] Gordon J B, Koutsopoulos H N. Automated inference of linked transit journeys in London using fare-transaction and vehicle location data[J]. Transportation Research Record Journal of the Transportation Research Board, 2013, 23(43): 17−24.

[12] Nassir N, Hickman M, Ma Z L. Activity detection and transfer identification for public transit fare card data[J]. Transportation, 2015, 42(4): 1−23.

[13] 胡郁葱, 梁杰荣, 梁枫明. 基于IC卡数据挖掘获取公交OD矩阵的方法[J]. 交通信息与安全，2012, 30(4): 66−70. HU Yucong, LIANG Jierong, LIANG Fengming. A way to get bus regional OD matrix based on mining IC card information[J]. Journal of Transport Information and Safety, 2012, 30(4): 66−70.

[14] 陈峥嵘. 智能公共交通系统数据分析方法与应用研究[D]. 南京: 东南大学, 2012. CHEN Zhengrong. Study on intelligent public transportation system data analysis methods and applications[D]. Nanjing: Southeast University, 2012.

[15] 胡继华, 邓俊, 黄泽. 结合出行链的公交IC卡乘客下车站点判断概率模型[J]. 交通运输系统工程与信息, 2014, 14(2): 62−67. HU Jihua, DENG Jun, HUANG Ze. Trip-chain based probability model for identifying alighting stations of smart card passengers[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(2): 62−67.

[16] 邓连波, 高伟. 基于换乘网络的城市轨道交通关联公交接驳线网优化[J].铁道科学与工程学报, 2012, 9(6): 77−83. DENG Lianbo, GAO Wei. Optimal design of feeder-bus network related to urban rail transit based on transfer network[J]. Journal of Railway Science and Engineering, 2012，9(6): 77−83.

[17] 王周全. 基于IC卡数据与GPS数据的公交客流时空分布研究[D]. 成都: 西南交通大学, 2016. WANG Zhouquan. Research on bus passenger flow space-time distribution based on IC card data and GPS data[D]. Chengdu: Southwest Jiaotong University, 2016.

[18] 陈绍辉, 陈艳艳, 赖见辉. 基于GPS与IC卡数据的公交站点匹配方法[J]. 公路交通科技, 2012, 29(5): 102−106. CHEN Shaohui, CHEN Yanyan, LAI Jianhui. An approach on station ID and trade record match based on GPS and IC card data[J]. Journal of Highway and Transportation Research and Development, 2012, 29(5): 102−106.

[19] 徐文远, 邓春瑶, 刘宝义. 基于公交IC卡数据的公交客流统计方法[J]. 中国公路学报, 2013, 26(5): 158−163. XU Wenyuan, DENG Chunyao, LIU Baoyi. Approach on public traffic passenger flow statistics based on IC data[J]. China Journal of Highway and Transport, 2013, 26(5): 158−163.

[20] 周和平,全维杰, 杨启福, 等. 基于区间情景的不确定性OD反推模型与算法[J].系统工程, 2013, 31(10): 75−80. ZHOU Heping, QUAN Weijie, YANG Qifu, et al. Uncertain optimization model and algorithm of estimating origin-destination matrices based on interval scenarios[J]. Systems Engineering, 2013, 31(10): 75−80.

[21] 全维杰. 区间不确定需求下的OD反推模型与算法研究[D]. 长沙: 长沙理工大学, 2013. QUAN Weijie. The model and algorithm for estimating origin-destination matrices under interval and uncertain demand[D]. Changsha: Changsha University of Science and Technology, 2013.

[22] 赵子衡. 区间不确定性优化的若干高校算法研究及应用[D]. 长沙: 湖南大学, 2012. ZHAO Ziheng. Research on efficient algorithms of interval-based optimization under uncertainty and its applications[D]. Changsha: Hunan University, 2012.

[23] Averbakh I, Lebedev V. Interval data minmax regret network optimization problems[J]. Discrete Applied Mathematics, 2004, 138(3): 289−301.

[24] Kasperski A. Discrete optimization with interval data: Minmax regret and fuzzy approach[J]. Distributed Computing & Networking, Internation, 2008, 4904: 393− 400.

[25] Kun An, Hong K Lo. Two-phase stochastic program for transit network design under demand uncertainty[J]. Transportation Research Part B, 2016, 11(84): 157−181.

The method of deriving passenger flow of bus alighting stops based on smart card data and interval uncertainty

LIU Wusheng, ZHOU Xiangdong, KUANG Kai

(School of Traffic and Transportation Engineering, Changsha University of Science and Technology, Changsha 410004, China)

In the context of large traffic data, for the existing passenger traffic OD derivation study passenger flow OD are fixed single value and the actual fluctuation interval value does not match the problem, the use of interval uncertainty theory, bus IC card data and GPS data combined, respectively To carry out on and off the station section of the passenger flow optimization, get off the bus station bus section OD. Integration of bus IC card data and GPS data, the use of interval uncertainty theory to get on the passenger flow interval value. The passenger travel behavior is analyzed, considering the passenger travel characteristics and passenger travel distance in the site to attract the weight, get off the station passenger flow derivation probability model, using interval uncertainty theory, get off the station passenger flow interval value. Taking the IC bus data and GPS data of 21 bus routes in Shenzhen as an example. Through the analysis of the rationality of the results, it shows that the OD of the passenger flow is more realistic, the algorithm is clear and the reliability is better.

Public transit OD; interval uncertainty theory; smart card data; GPS data; alighting location

10.19713/j.cnki.43−1423/u.2018.11.032

U49

A

1672 − 7029(2018)11 − 2988 − 07

2017−09−28

国家自然科学基金面上资助项目(61508065，51178061)

柳伍生(1976−)，男，湖北监利人，副教授，博士，从事交通运输规划与管理、公共交通网络设计、交通行为分析等方面的研究；E−mail：lwusheng@163.com

(编辑 阳丽霞)