基于系统动力学与logit模型的驮背运输运价研究

冯芬玲，余海军



基于系统动力学与logit模型的驮背运输运价研究

冯芬玲，余海军

(中南大学 交通运输工程学院，湖南 长沙 410075)

利用logit模型，建立驮背运输与公路运输货运需求分担模型，结合系统动力学，形成驮背运输属性与需求之间的动态反馈仿真模型。在京沪通道货运需求增长率为“高”、“中”和“低”3种情形下，分别对政府定价、市场化运价和市场+调控运价3种运价体制进行仿真，得出3种体制下的较优运价策略，分析3种运价体制的优缺点，提出驮背运输运价发展建议。驮背运输价格仿真模型，提供了一种价格仿真方式，仿真结果为驮背运输的调整提供了参考。

驮背运输；运价；logit模型；系统动力学

《“十三五”现代综合交通运输体系发展规划》提出“布局网络化、服务一体化、管理智能化、发展绿色化”的综合交通运输体系发展导向，多式联运是实现“四化”发展的重点。驮背运输，作为公铁联运的一种方式，以铁路平车运输汽车半挂车、汽车整车，结合公路运输与铁路运输的优势，实现公路“门到门”运输，是货物运输向现代物流业发展方向。我国没有开展驮背运输，现状空白，同时，我国铁路市场化改革进入深水区，铁路企业运价自主权扩大，运价弹性增大，铁路运价由政府定价向市场化运价转型。在此背景下，有必要对驮背运输的运价政策进行研究，为驮背运输进入市场提供参考。在市场化运价环境，驼背运价由铁路运输供需比、可替代运输方式竞争价格、政府调控等因素控制。驮背运输以铁路线路为依托，具有固定的路线，运输需求来源于通道的整车货物，logit模型在研究客货运输方式分担率上应用成熟。Ravibabu[1]建立港口集装箱货物在内陆运输选择的NL模型，发现运价和时间是货主选择的主要影响因素。宋睿等[2−3]分别建立货物运输链的多层logit模型和混合logit模型，研究运输链货运方式选择的关键决定因素。logit模型确定运输方式的选择概率，是静态、单向的决策过程。实际中，运输方式的选择是动态变化的，既有时序的动态变化，也有运输方式选择和决策属性相互作用的动态变化，系统动力学常用于处理动态、反馈问题。Shepherd[4]综述了系统动力学在交通运输上的应用。LIU等[5]运用系统动力学仿真了拥堵定价策略对缓解城市交通拥堵的动态影响。孙广林等[6]仿真了不同社会经济水平下的城市公交的价格策略。市场经济下，供需比的变化影响运输方式的决策属性(价格、运能等)，决策属性的调整影响运输方式的需求。本文结合logit模型和系统动力学优势，建立通道下驮背运输决策属性与运输方式分担率的动态反馈仿真模型，研究驮背运输不同运价策略的差异。

1 京沪通道货运方式分担率的logit模型的建立

logit离散选择模型的理论基础是“消费者在选择时追求效用最大化”，交通出行中，出行者从交通方式集中选择效用最大的交通方式。运输方式选择集为A时，第批货物选择运输方式的概率如式(1)P所示，U为第批货物选择运输方式的效用值。效用值包括非随机变化部分V和随机变化部分，如式(2)所示。当随机效用服从相同的二重指数分布式，方式的被选择概率可表示为式(3)。

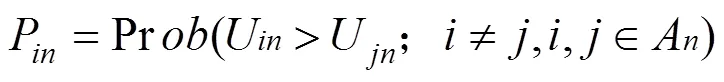
基于假设(1)，2015年京沪通道开行驮背运输。运输方式选择集为{驮背运输、公路运输}。综合现有通道货运方式选择研究和驮背运输特点，选取式(4)形式表达效用值固定项V，式中S，C，T，F，R，Q和H依次表示第批或第种运输方式的安全性、运价、作业完成时间、客户感知服务质量、准点率、是否需要换乘和是否实现“门到门运输”，其中，Q和H为0和1变量，取值1表示“是”。

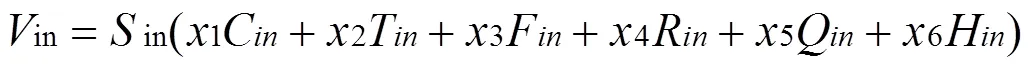
2 驮背运输系统动力学模型的建立

2.1 模型假设

1) 2015年京沪通道开行驮背运输。

2) 假设上海至北京的驮背班列为直达班列。

3) 驮背班列基价1的最小值为0.1。

2.2 系统边界的确定及子系统的划分

驮背运价仿真研究是多层次的复杂系统，根据国外驮背运输的开行和我国铁路运输管理，将驮背运输价格仿真模型划分为驮背运输、驮背服务、驮背市场和驮背运价调整四大子系统，子系统内的主要要素及相互关系如图1(a)所示。

根据子系统之间物质、信息流的流动、反馈，得到如图1(b)驮背运价仿真模型因果关系图，运价调整、运能增长调整为仿真调整变量。

2.3 系统流图及方程

驮背运输价格仿真系统动力学模型中，包含logit运输方式选择模型，图2为驮背运输直达班列龙体模型效用值的流图模块，公路运输效用值流图具有相同形式。

基于图1中子系统之间的关系、主要因果反馈环，结合国外驮背运输的实际情形[7]，采用vensim- ple软件制定图3的系统动力学流图。

(a) 子系统划分；(b) 因果回路

图2 直达班列效用值系统流图

图3 驮背运输运价系统流图

3 驮背运输运价仿真及仿真结果分析

3.1 模型参数的确定

3.1.1 logit模型系数的确定

决策属性的系数1~6常有统计回归和专家打分2种确定方法，本文的系数基于专家打分，采用层次分析法确定，取值如表1所示。

表1 系数权重

Table 2 Coefficient weight

确定决策属性系数后，需要对决策属性数值进行标准化处理。文献[8]提供的数值处理方法,将决策属性的实际数值归一化，极大地降低了属性的灵敏度。在BL模型中，效用值与决策属性值并非线性相关。以运价为例，运价差值不大时，运价对分担率的影响较小，随着运价差值的增大，对分担率的影响逐渐增加。本文采用式(5)~(6)分别对逆属性(效用值与属性值负相关)、正属性(效用值与属性值正相关)处理，1和2为驮背运输、公路运输的决策属性输入值，1和2表示驮背运输、公路运输决策属性数值，1和2为待确定参数，表示属性的数量。

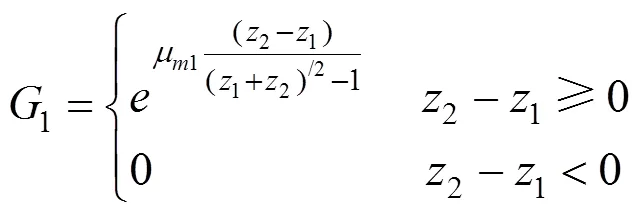
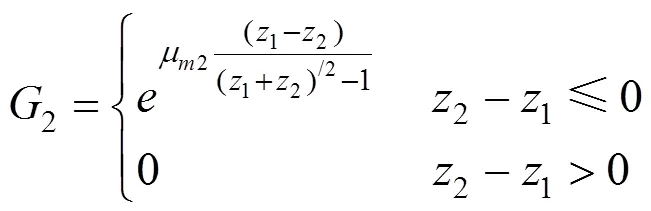
μ1和μ2确定决策属性对分担率的灵敏度，通过系统动力学模型测试求得。以运价参数11和12为例，市场调查发现，公路运价在0.3~0.4，当驮背运价为0.6~0.8，驮背运输选择概率为0.05，当驮背运输运价为0.1~0.2，驮背运输选择概率为0.95，求得μ1=2.744 6，μ2=4.097。其他μ1和μ2通过相同方法求得，结果如表2所示。

表2 参数μm1和μm2取值

3.1.2 系统动力学仿真模型数据的确定

1) 仿真时间及步长

京沪通道驮背运输仿真模型以2015年为时间起点，2055年为终点，1 a为时间步长。

2) 京沪通道货运需求增长率

考虑京沪通道整车货运需求增长率高、中和低3种可能情景，“高增长率”情景，货运需求延续1996~2015年全国货运量增长率均值0.065，标准差0.53的正态分布；“中增长率”情景，根据发展预测，2015年以后我国经济、货运需求将保持低位增长，增长率服从均值0.02，标准差0.25的正态分布；“低增长率”情景，货运需求出现负增长时，增长率服从均值−0.035(1996~2015年中的货运量最低增长率)、方差2的正态分布。3种情景下的需求变化情况如表3所示。

表3 通道整车货运需求增长率

3) 公路运输、驮背运输的属性值

公路、驮背运输技术参数如表4所示。通道整车货运需求、公路运价按照式(7)~(8)计算，公路趋势运价等于文献[9]提供的全国公路运价，变动运价按照式(9)计算。

表4 公路、驮背运输相关参数

整车货运需求=货运密度[10]/平均运输时间

*365 d*24 h*整车比率*需求占比[11](7)

公路运价=公路趋势运价+公路变动运价 (8)

公路变动运价=(通道货运实际增长率−

“高”增长率)/0.02*0.01−0.05≤

公路变动运价≤0.05 (9)

3.2 仿真结果分析

3.2.1 驮背运输政府定价、市场化运价、市场+调控运价的差异

利用驮背运输仿真模型，分析驮背运输“政府定价”、“市场化运价[12]”、“市场+调控运价”差异。《中华人民共和国铁道部铁路货物运价规则》规定，铁路运价计算如式(10)所示，基价1为运输费率，基价2为装卸费率。驮背运输其他费率采用铁路整车6号运价，基价2为50元，基价1为仿真变量。政府定价体制下，基价1维持不变，市场运价体制下，基价1随市场供需变动，文献[13]给出市场环境下价格与供需比的一般关系。市场+调控体制下，对基价1与运能的波动予以调控。3种模式的主要区别如表5所示，其中，和为未知变量。

运价=(基价1*运距+基价2)/运距+电气费率+

建设基金费率+新路建设费 (10)

表5 3种运价体制的差异

其中：直达班列运价增长=表函数[(0.2,0.05), (0.5,0.04),(0.9,0.02),(1,0)]

直达班列运价降低=表函数[(1,0),(1.1,−0.02),(1.5, −0.04),(1.8,−0.05),(2,−0.06)]

3.2.2 3种运价体制下运费收入差异及结果分析

京沪通道货运需求高、中和低3种增长情况下，班列累计收入如图4所示，3种运价体制累计收入情况依次为：市场+调控收入＞政府定价收入＞市场运价收入、市场+调控收入＞政府定价收入＞市场运价收入、政府定价收入＞市场+调控收入＞市场运价收入。其中政府定价收入是该体制下的最佳收入，市场化运价收入、市场+调控是一种较优 收入。

高增长率情景，政府定价、市场化运价体制下，驮背运能增长滞后于需求增长，运价持续增高，驮背运输市场份额降低，运价和运量不是最佳匹配。市场+调控体制下，一方面提高运能的增长速度，另一方面限制运价的增长速度，运能与运价能相互协调配合。

中增长率情景，政府定价、市场化运价体制下，驮背运能还是滞后于需求，但是差值较小，影响驮背货运需求的主要因素是公路运价。市场+调控体制下，限制驮背运价波动幅度，实现驮背货运需求与运价的稳定协调。

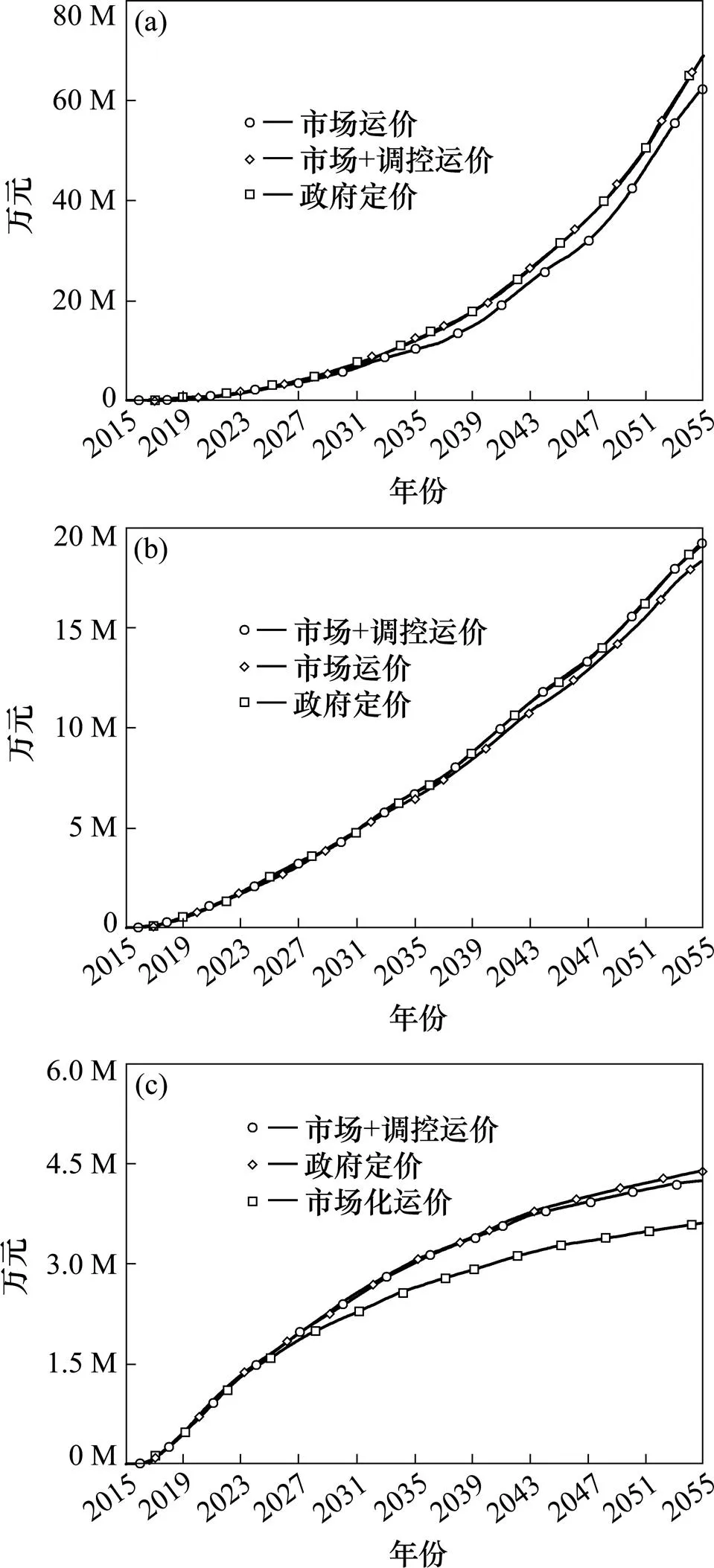
(a) 高增长率；(b) 中增长率；(c) 低增长率

低增长率情景需求负增长，运能大于需求。市场运价体制下，运价降低，实现运能的利用。市场+调控体制下，限制运能在前期的增长，降低运价降低幅度，使运价与运量协调。

3种运价体制下的运价、运能相关参数如表6所示，所有参数都是在各种体制下多次仿真下得到的，该结果可以为上海至北京驮背运输直达班列的运价决策提供参考。

表6 3种运价体制下的运价、运能相关数据

3.2.3 3种运价体制下的运价、市场份额和驮背运输运能利用的差异

3种运价体制收入上的差异归根结底是由于其在运价、市场份额方面的差异。政府定价体制下，运价维持不变，价格缺乏市场弹性，运能变化与市场总体趋势脱节，虽有稳定的驮背运输收入，但市场份额波动大(图5(b))，造成运能的不足(高增长率下)或运能的剩余(低增长率下，图5(c))。市场运价体制下，运价随供需比波动，而驮背运能不能适应市场规律。驮背运能造价高，运能增长受到生产能力制约；在退役期前，驮背运能只能非负增长。驮背运能增长滞后需求增长，运价波动大(图5(a))。市场+调控运价体制，通过运价、运能的调控，实现运价变化、运能增长与市场需求趋势的匹配既实现运费收入的优化，也保证了驮背运能的利用 (图5(c))。

3.2.4 驮背运输价格策略的建议

综合3种情景下，3种运价体制的收入、市场份额的差异结果，政府定价体制不能反映市场供需的变化，市场化运价体制难以兼顾运价与运能的协调，市场+调控体制的市场调控需要建立在对通道整体需求增长趋势把握。建议在未来驮背运输的运价制定中：

1) 采用“市场+调控”的运价体制。驮背运价与公路运价的大小，应当根据货运需求决定，当货运需要增长率高，驮背运价可适当高于公路运价。

2) 做好市场调研，根据市场变化，优化驮背运价的调控机制。

3) 合理协调运能与运价的调节作用，能够实现运能的充分利用和运输收益的提高。

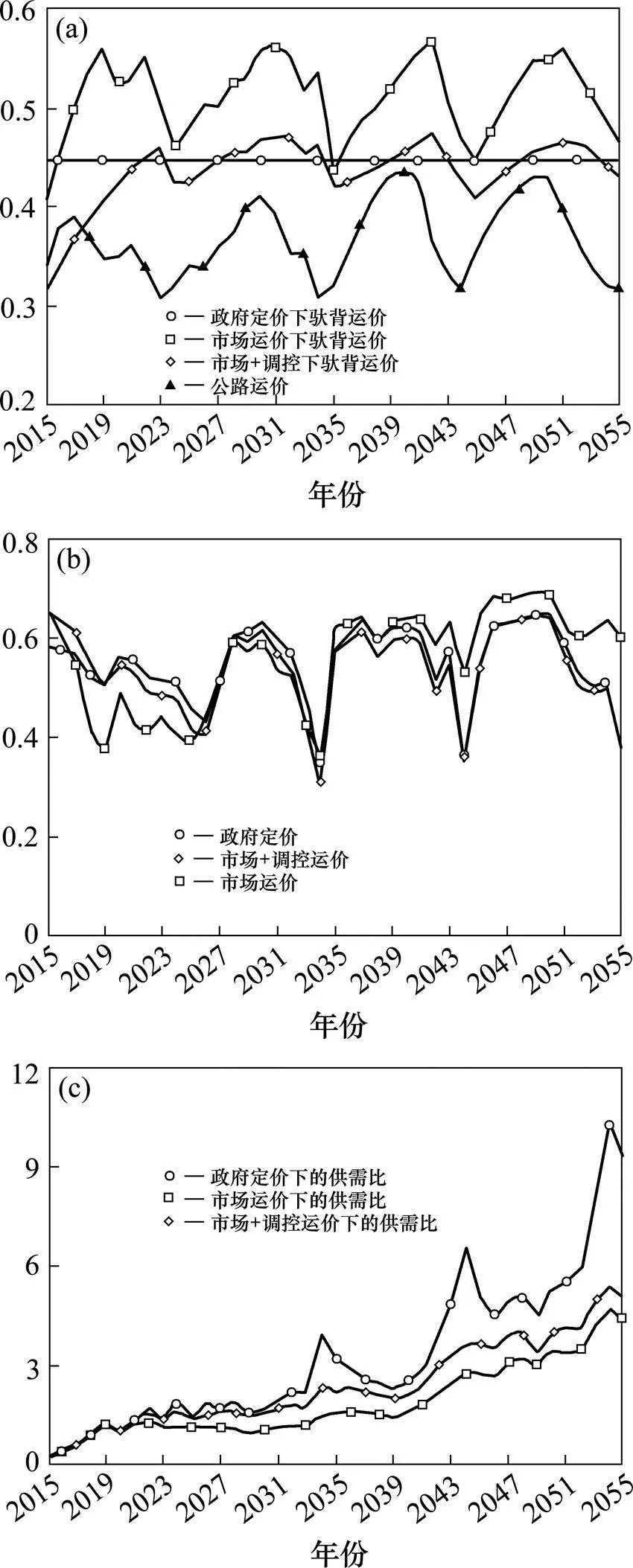
(a) 高增长率运价对比；(b) 中增长率市场份额对比；(c) 低增长率供需比对比

4 结论

1) 政府定价体制，运价缺乏市场弹性，易造成驮背运输市场份额的不稳定。市场化运价体制，运价与运能难以同时匹配市场需求规律，难以获得较高的运费收入。市场+调控运输体制，尽力避免市场化运价体制的弊端，使运价与运能的变化符合市场需求规律，在获得较高收入的同时，稳定驮背运输市场份额，提高驮背运输运能利用。

2) 在未来驮背运输的开行中，宜选用“市场+调控”运价体制。做好市场调研，不同需求增长时，采用合理的定价和调控手段，做到运能利用和运输收益的最大化。

[1] Ravibabu M. A nested logit model of mode choice for inland movement of export shipments: A case study of containerised export cargo from India[J]. Research in Transportation Economics, 2013, 38(1): 91−100.

[2] 宋睿, 孙焰. 基于多层logit模型的货物运输链选择研究[J]. 武汉理工大学学报(交通科学与工程版), 2014(4): 792−795. SONG Rui, SUN Yan. Research on the selection of freight transport chain based on multi-layer logit model[J]. Journal of Wuhan University of Technology, 2014(4): 792−795.

[3] 张戎, 诸立超, 陶学宗. 基于混合logit模型的饶甬运输链选择行为分析[J]. 交通运输系统工程与信息, 2014, 14(1): 138−143. ZHANG Rong, ZHU Lichao, TAO Xuezong. Analysis of Raoyong transportation chain choice based on mixed multinomial logit model[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(1): 138−143.

[4] Shepherd S P. A review of system dynamics models applied in transportation[J]. Transportmetrica B Transport Dynamics, 2014, 2(2): 83−105.

[5] LIU S, Triantis K P, Sarangi S. A framework for evaluating the dynamic impacts of a congestion pricing policy for a transportation socioeconomic system[J]. Transportation Research Part A Policy & Practice, 2010, 44(8): 596−608.

[6] 孙广林, 王健, 胡晓伟. 城市公交价格组合策略的系统动力学建模与仿真[J]. 交通运输系统工程与信息, 2010, 10(6): 121−127. SUN Guanglin, WANG Jian, HU Xiaowei. System dynamics model and simulation of integrated price strategies of urban public transport[J]. Journal of Transportation Systems Engineering and Information Technology, 2010, 10(6): 121−127.

[7] Seidelman C. 40 years combined transport road-rail in Europe: from piggy-back transport to an intermodal transport system[M]. Brussels: International Union of Combined Road-Rail Transport Companies, 2010.

[8] 宋建强, 鲍学英, 王起才, 等. 基于Influ-Logit模型的兰州至中川铁路货运量分担率研究[J]. 铁道科学与工程学报, 2016, 13(1): 176−180. SONG Jianqiang, BAO Xueying, WANG Qicai, et al. Study on the share rate of Lanzhou to Zhongchuan railway freight volume based on Influ-Logit model[J]. Journal of Railway Science and Engineering, 2016, 13(1): 176−180.

[9] 顾敬岩, 吴群琪. 我国公路货运市场价格的演进趋势、问题及对策[J]. 交通运输系统工程与信息, 2013, 13(6): 191−197. GU Jingyan, WU Qunqi. Price evolution trends, problems and countermeasures of china road freight market[J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13(6): 191−197.

[10] 中华人民共和国交通运输部. 2015中国高速公路运输量统计调查分析报告[M]. 北京: 人民交通出版社, 2016. Ministry of Transport of the People’s Republic of China. The Report of China’s Highway Traffic Volume Survey Analysis in 2015[M]. Beijing: China Communications Press, 2016.

[11] 中华人民共和国交通运输部. 全国公路水路运输量专项调查资料汇编[M]. 北京: 中国经济出版社, 2009. Ministry of Transport of the People’s Republic of China. The Compilation of Special Survey Data on National Highway and Waterway Traffic[M]. Beijing: China Economic Publishing House, 2009.

[12] 丁永民, 黄鑫. 关于铁路运输市场价格形成机制的研究[J]. 铁道运输与经济, 2015, 37(12): 1−7. DING Yongmin, HUANG Xin. Study on tariff forming mechanism of raitway transport market[J]. Railway Transport and Economy, 2015, 37(12): 1−7.

[13] 杨菊红, 郝睿, 王旭明, 等. 基于产品定价机制的博弈模型[J]. 复杂系统与复杂性科学, 2013, 10(2): 44−51. YANG Juhong, HAO Rui, WANG Xuming, et al. A game model based on pricing mechanism[J].Complex Systems and Complexity Science, 2013, 10(2): 44−51.

Research on piggyback transport price based on system dynamics and logit model

FENG Fenling, YU Haijun

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

Based on the logit model, this paper built a model of freight demand sharing model between Piggyback transport and Highway freight. Then, a dynamic feedback simulation model, about system dynamics, between property and demand of Piggyback transport was formed. In the case of “high”, “middle” and “low” of freight demand growth rate in the Beijing-Shanghai corridor, this paper simulated Government pricing, Market freight rate and Market & Regulation freight rat. The optimal price strategies under three kinds of freight rate system were obtained through the simulations. This paper analyzed the advantages and disadvantages of the three kinds of freight rate system, and put forward suggestions for the development of piggyback transport price. The simulation model of Piggyback transport freight rate provides a method of price simulation, and the simulation results provide a reference for Tariff Strategy of Piggyback transport.

piggyback transport; freight rate; logit model; system dynamics

10.19713/j.cnki.43−1423/u.2018.11.031

U294.1

A

1672 − 7029(2018)11 − 2980 − 08

2017−09−19

国家重点研发计划项目(2018YFB1201402-10)

冯芬玲(1973−)，女，河北邯郸人，副教授，博士，从事交通运输规划与管理研究；E−mail：ffl0731@163.com

(编辑 阳丽霞)