放飞思维 精彩纷呈——“超级全能生”全国卷26省3月联考乙卷理科第15题探析与教学启示

山东 尹承利

“超级全能生”3月联考成功举行，通过联考及时检测了学生复习备考的情况.在试卷中有许多蕴涵丰富数学思维价值的试题，本文根据数学全国乙卷理科第15题的考情及所潜在的思维功能、应用功能及拓展功能作如下探析.

一、试题呈现

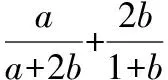
二、考情分析

这是一道有着深度思维背景的考题，从考试成绩分析的数据看，该题平均得分率、区分度均偏低，由下表便可窥见一斑.

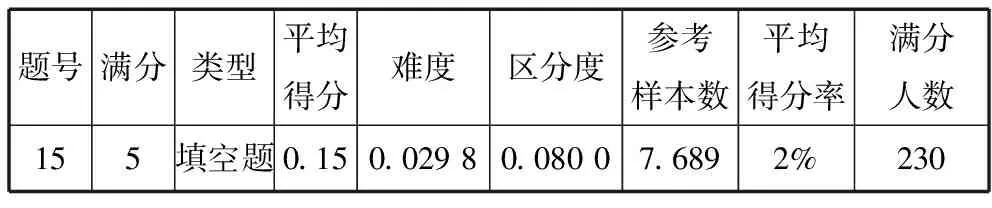
题号满分类型平均得分难度区分度参考样本数平均得分率满分人数155填空题0.150.029 80.080 07.6892%230

由于是填空题，我们无法从学生卷面去找到学生答题不理想的原因！但我们可以试着从试题本身的结构形式和思维量等视角略作剖析：

1.该题难度大，体现在该题的是“二元分式型的条件最值”问题，并由此使得变形、整理过程冗繁，运算量大，技巧性强.因而大多数的学生“望题生畏”、“望题兴叹”，出现解答的畏难情绪或不敢涉猎该题的情况也就不足为怪了！

2.难道说该试题就不可取吗？恰恰相反，该题是一道能充分考查学生思维能力的优质试题，命题老师设置精当、颇具匠心.那是什么原因导致这样的局面呢？笔者个人认为，问题还是出在备考上，就该题而言，在备考方面无论是学生的知识和方法的积累、储备，还是学生应对思维量大的问题，分析问题的背景、将问题转化处理的能力等都还是有所欠缺的，当遇到情景相对新一些的问题就不知所措、束手无策了.其实，解答本题时，消元→化为一元函数式→利用单调性求解；或者，代换“1”→待求式通分整理→齐次化→分离常数→直接运用基本不等式，或换元后运用基本不等式，或转化为一元二次方程用判别式求解，这两方面的途径都纯属再正常不过的解题思路.至于学生作答的这么不理想，不能不说是有些遗憾的，这也为我们后面冲刺阶段的备考敲响了警钟，理应引起教师的重视.

三、解法探析

为发挥该试题的最大效益，笔者特从不同的视角给出解答该题的思维分析和几种不同的解法，供参考.

1.思维分析

解答该题如何寻找切入点呢？条件式是整式和的形式，结论式是分式和的形式.在求最值的一些常用方法中，比如利用二次函数的最值、三角函数的最值、基本不等式等求最值，依据目标式的结构特点，我们首要想到的是运用基本不等式，这样就初步确定求解该题的基本方向，当然也可能会有其他的方法.其次，从条件式2a+b=1获得的信息，可大致有两种具体求解的路径：一是消元，转化为一元问题求解，根据变形、转化待求分式的情况或利用单调性，或利用基本不等式；二是，由于待求分式第二项的分母中有“1”，这就暗示可以进行“1”的代换，“1”的代换后就将分式化为了齐次式，进而或通分并分离常数，或换元转化，变形出基本不等式的结构求解.

求解这类二元最值问题的思维导图：

由于求解该题的方向、方法均确定了，便有了下面具体的求解方法.

2.解法赏析

分析1.首先进行“1”的代换：1=2a+b，化为关于a,b的二次齐次分式后变形为基本不等式的结构形式，利用基本不等式求得最值.

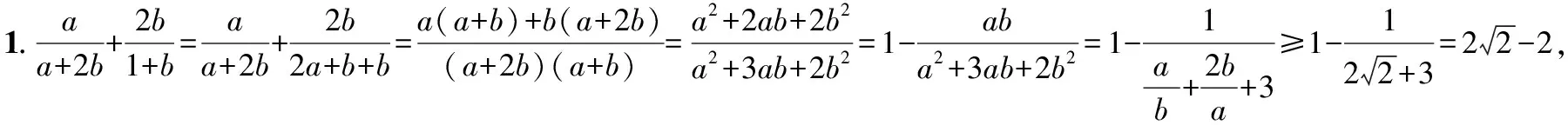
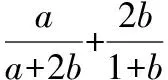
【点评】该解法将目标式整理为关于a,b的二次齐次分式后，分离常数，进而转化为运用基本不等式的结构形式求解，技巧性较强.

分析2.首先进行“1”的代换：1=2a+b，化为关于a,b的二次齐次分式后，进行双变量换元，变形为基本不等式的结构形式，利用基本不等式求得最值.

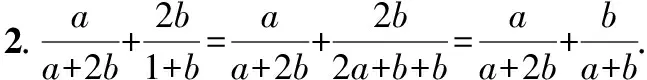
令a+2b=m,a+b=n(m>0,n>0)，则a=2n-m,b=m-n，所以

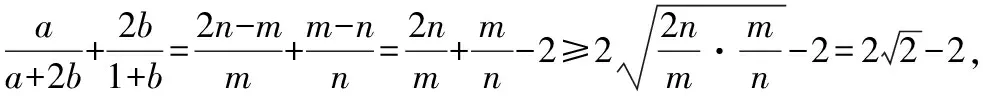
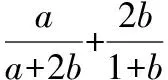
【点评】对于通过“常值代换”转化成两项一元齐次分式和的一类二元条件最值问题，利用双变量换元法求解十分奏效.

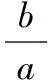
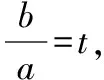
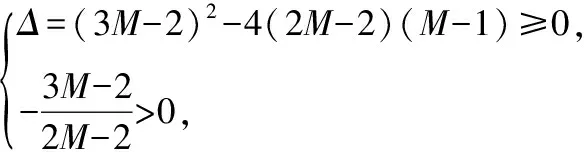
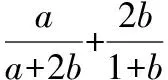
【点评】该解法把目标式变形整理作比后，再换元化为关于新元的一元二次方程，利用判别式法求解.

分析4.由2a+b=1，得b=1-2a，消元转化为关于a的二次齐次分式后，利用导数求解.

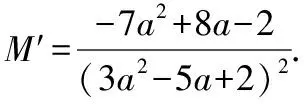
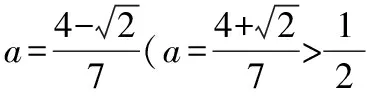
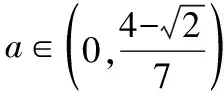
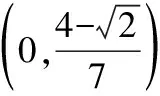
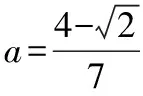
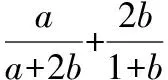
【点评】该解法通过消元，化为关于a的一元函数式，求导利用单调性求解.这也是求解二元条件最值问题常用的一条途径.

四、问题变式

俗话说：铁打的盘，流水的兵.高考中不变的是知识，变化的是情景的呈现形式和问题的结构方式.这就要求我们面对典型的数学问题时，能突破常规，多做变式工作，使学生做一个题，会一类题、一串题.

仅仅改变一下问题的条件式的背景，可有变式1～4.

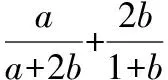
略解：由点(a,b)在线段2x+y=1(x>0,y>0)上，得2a+b=1(a>0,b>0).下同上面的方法.

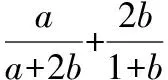
略解：由点(1,1)恒在函数y=2ax+b(a>0且a≠1,b>0)的图象上，得2a1+b=1(a>0且a≠1,b>0)，即2a+b=1(a>0且a≠1,b>0).下同上面的方法.

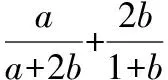
略解：因为m·n=-1，所以-2a-b=-1，即2a+b=1(a>0,b>0).下同上面的方法.

所以2a+b=1(a>0,b>0).下同上面的方法.

问题的条件式不变，改变待求的分式的形式，可有变式5.

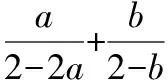
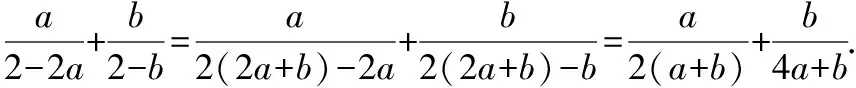
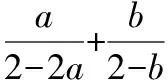
注：本题是将目标式化为两个一次齐次分式和的形式后，利用双变量换元，转化为基本不等式的结构求解的.

既稍加改变条件式，同时又改变待求的分式，可有变式6.

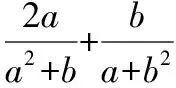
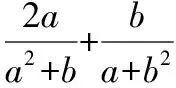
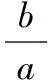
逆向考虑问题，可有变式7.

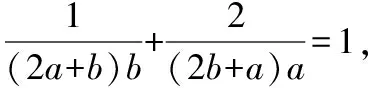
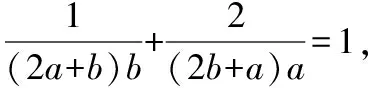
设2a+b=m，2b+a=n(m>0,n>0)，

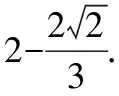
注：已知条件式是“和的形式”，目标式是“积的形式”，从而联想到基本不等式，采用“1的代换”，把目标转化为一次齐次分式后，进行双变量换元，问题得以解决.

将问题中的条件等式换为不等式，同时改变待求的分式，可有变式8.

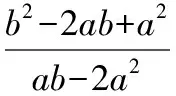
设u=t-2(u>0)，则

注：本变式的条件式是不等关系式，应特别注意换元后新元的范围跟进.本题解法中进行了两次换元，最后转化构造出基本不等式的结构形式求解.

若进一步强化条件，将问题中的条件等式加强为不等式，同时改变待求的分式，可有变式9.

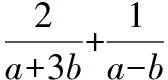
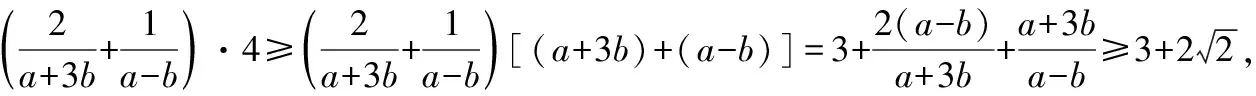
注：首先分析出条件中的不等式与待求式在结构上的联系，然后进行代换，构造出基本不等式的结构，利用基本不等式放缩求解.运用放缩技巧时，要注意放或缩的一致性，并且特别注意各步的放或缩是否可以同时取得等号.

二元条件最值问题，不止是“分式型”，在高考或各地模拟题，或是各类竞赛题中“整式型”的问题也常出现，结合联考题化为二次齐次式的式子，这里可有变式10.

变式10.已知正实数a,b满足a2+3ab+2b2=1，则a2+2ab+2b2的最小值是 ．

解析：(单变量换元法)由a2+3ab+2b2=1，得(a+b)(a+2b)=1.

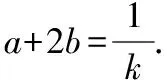
由于a,b均为正实数，则有a+b>0，所以k>0.

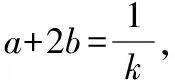
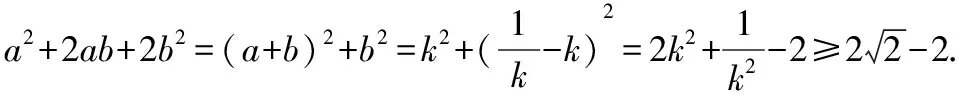
五、题型规律

二元函数的条件最值问题，因其注重考查考生的综合思维能力，具有很好的区分功能，能够很好地考查学生的数学思维能力，一直备受命题者的青睐.此类问题求解时往往技巧性特别强，学生不易掌握.储存、掌握这类问题的模式和解决的方法是解答的关键.

根据问题的结构特征，解答二元函数的条件最值这类问题所用的数学思想是：常量(“1”)代换和齐次化；所用的方法途径通常有三个：①将函数式变形转化后，直接利用基本不等式，如联考题解法1；②将函数式变形转化后，消元转化为一元函数利用基本不等式或函数的单调性，如联考题解法4；③将函数式变形转化后，换元，利用基本不等式求解，如联考题解法3，或转化为一元二次不等式利用判别式工具求解，如联考题解法2；其中换元又分为单变量换元，如变式10的解法，双变量换元，如联考题解法2.

六、教学启示

如何利用“变式教学”来促进学生数学核心素养的形成和发展，是当前数学教学研究的重要课题，也是《普通高中数学课程标准》的要求，为此《教学考试》为我们提供了一个良好地展示自我的平台，我们应怀有一颗虔诚的心，顺势而为.

1.数学问题的“变式教学”，不能仅仅满足让学生掌握几种解题方法，更重要的是着眼于学生的进一步发展，通过各种方法的对比，教会学生如何挖掘问题条件蕴含的内容，学会看准目标，优化解题思路.当然，过程体会与循序而导对于学生的思维品质提高、解法自然生成也有决定性的作用.我们在关注解法的同时，更让学生经历“如何想到这样解”的思路历程.这样的话，解题的思想方法才会得到较充分的落实.