研究圆锥曲线的一些结论的必要性

安徽 乔明东 张 威

圆锥曲线是高考考查的重点和难点，也是热点，是高考中区分度较大的题目，题型有选择题、填空题、解答题，难度一般是中档以上.而在高考真题中一般是以圆锥曲线的定义、简单几何性质、直线与圆锥曲线的位置关系为命题角度，其中一部分是有着很强的结论性背景的题目.可见研究圆锥曲线的一些结论是必要的.那么研究这些结论到底有什么好处呢？笔者有以下几点认识.

一、“秒杀”客观题

在高考数学试卷中，客观题所占的分值比较高，考查的知识覆盖面广，小巧灵活，又有一定的综合性和深度，能否快速准确的得到答案，为解答题赢得更多的时间，就显得至关重要.而客观题中的圆锥曲线题一般计算都稍显复杂，如果采用小题大做的方法，是不明智的选择.比如2018年高考全国卷Ⅲ理科第16题.

【例1】已知点M(-1，1)和抛物线C:y2=4x，过C的焦点且斜率为k的直线与C交于A，B两点．若∠AMB=90°，

则k= ．

【题目分析】此题是填空题的压轴题，从所处的位置来看，就使得一部分学生畏缩不前.同时如果作为解答题来求解，又要花费很长时间，而且可能由于计算的失误，导致结果错误.但是如果理解此题的结论背景，就可以快速求解.那么此题隐含了什么样的结论呢？具体如下：

若抛物线C：y2=2px(p>0)的焦点为F,过F且斜率为k的直线l与C交于A,B两点.

【评注】可以发现此题利用结论进行求解是非常快的，所以对于客观题尽可能的采取小题小做，或者小题不做的策略，快速智取.像这样具有结论性背景的圆锥曲线客观题在2018年高考真题中比比皆是.

二、增强解题的信心和提供解题思路

在高考数学试卷中，圆锥曲线解答题一般设置两问，尤其是第二问，思维性和计算性要求都很高，属于较难题.在求解的过程中，可能出现有思路，而无法运算到底，也可能一点思路都没有.而如果了解了题目的结论性背景，不仅可以提供思路，而且还可以提前得到答案.比如2018年高考全国卷Ⅰ理科第19题.

(Ⅰ)当l与x轴垂直时，求直线AM的方程；

(Ⅱ)设O为坐标原点，证明：∠OMA=∠OMB.

【题目分析】在近几年高考中，圆锥曲线作为解答题一般出现在第20题，而2018年却出现在第19题，对于题目本身难度虽有所降低，但从整卷位置看来，此题权重很大，所处的位置是一个基础分和拔高分的分水岭.同时在大多数学生的思维中，圆锥曲线属于难题，还没有审题，就有畏难情绪，极易让学生心生“澎湃”，所以是否能够正确解答和快速解答就会直接影响学生解答其余题目的信心.那么如果知道此题的结论性背景，无疑给自己打了一针“强心剂”，同时如果进一步了解结论的推导过程，则题目即可迎刃而解了.那么此题有什么样的结论性背景呢？具体如下：

对于例2，从所给的条件来看，完全符合上述结论，当发现该题的结论性背景时，内心一片“窃喜”，同时增加了一种信念——这题会做.再结合该结论的推导过程(利用直线l的方程与椭圆方程联立，再利用韦达定理建立未知量的等量关系，从而得到kMA+kMB=0，继而得到∠OMA=∠OMB)，故可以对例2进行快速求解，具体如下：

因为直线l过x轴上定点，故直线l的方程可设为x=my+1，A(x1,y1),B(x2,y2)，

所以即证明y1(x2-2)+y2(x1-2)=0，即只需要证明y1(my2-1)+y2(my1-1)=0，

当m=0时，由椭圆对称性可得∠OMA=∠OMB；

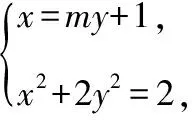
又当直线l与x轴重合时， ∠OMA=∠OMB=0°.

综上所述∠OMA=∠OMB.

【评注】可以发现，掌握了结论及其推导过程，既增强了解题的信心，又快速有了解题思路，这个在高考中是多么难能可贵.同时此题解法较多，在此只给出一种比较常见的通法.同时在求解的过程中，要特别注意对斜率的讨论，以免由于不严谨被扣分.

三、能快速抓住题目的本质，继而解决一类题

如何解决一类题，笔者认为只要抓住这一类题的本质即可.那么什么是题目的本质呢？本质就是事物的根本性质.认识事物的本质就是把握事物的必然性，规律性.本质隐藏在现象中，不能被感官直接把握，只能由思维来揭示.为此我们在分析和解决数学问题时,应通过对题目条件和结论的细致观察，充分比较，深入分析，广泛联想，抓住其本质.只有这样，我们才能提纲挈领,居高临下地洞察问题的症结，从而制定出一种解决问题的方法，即通性通法.而以结论为背景的圆锥曲线题，其本质即为其结论，以同一个结论为背景的不同题目很多，绝大多数只是设问角度不同，只要抓住其结论及推导方法，问题就能迎刃而解.比如下面这道以例2所对的结论为背景的原创题.

(Ⅰ)求C的方程；

(Ⅱ)设直线l与x轴的交点为M，当直线l变化(l不与x轴重合)时，若|MA||PB|=|MB||PA|,求点M的坐标．

(Ⅱ)设A(x1,y1)，B(x2,y2)，l的方程为x=ky+m，代入椭圆方程并整理得

(3k2+4)y2+6kmy+3m2-12=0，

由Δ=(6km)2-4(3k2+4)(3m2-12)>0，

解得m2<3k2+4，

因为∠OPA=∠OPB，所以kPA=-kPB，即kPA+kPB=0.

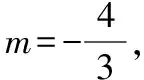
【评注】通过此题可以发现，只要掌握了这个结论，那么以这个结论为背景命制的试题，其解法基本上是一样的.同样的这个结论也可以推广到以双曲线、抛物线为背景的试题中去，比如2018年高考全国卷Ⅰ文科第20题.

四、拓宽原创试题的“道路”

利用教师个人命制的原创试题来检验和巩固学生所学的知识是教师的一项重要的、经常性的工作.而拓宽个人原创试题的“道路”更是教师一项重要的和长期性的工作.笔者认为掌握圆锥曲线的一些结论，是拓宽圆锥曲线题的原创“道路”的一种重要方法.如例3就是以圆锥曲线的一个结论为背景的原创试题，再比如2018年高考全国卷Ⅱ文科第11题.

【例4】已知F1,F2是椭圆C的两个焦点,P是C上的一点,若PF1⊥PF2,且∠PF2F1=60°,则C的离心率为

( )

【题目分析】此题考查椭圆的简单几何性质，难度属于中档.要想以此为背景进行原创试题或变式，那么必须要抓住题目的实质，而此题的实质恰是椭圆的一个结论，具体如下：

通过上述结论，可以原创如下试题：

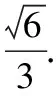
答案：∠F2PF1=120°.

【评注】通过上述原创试题，可以发现，不仅可以通过改变题干，也可以通过改变设问角度进行原创，只要抓住这个结论即可.

五、提升分析问题和解决问题的能力

发现问题、分析问题的目的是为了解决问题.能否解决问题,就必须要从题干上、设问上和题目所蕴含的结论上入手，这样才能真正地解决问题.而如何挖掘出题目所蕴含的结论，需要对题目进行反思,反思的过程即是一个发现问题和分析问题的过程，这个过程不仅提升了分析问题和解决问题的能力，也巩固了题目本身所对应的知识.