超几何分布与二项分布易混问题剖析
2018-12-07甘肃魏正清
甘肃 魏正清
超几何分布与二项分布是常见的离散型随机变量的分布问题,一直是高考考查的热点.但有不少学生在求解离散型随机变量的分布列时,时常把超几何分布问题当二项分布处理,或把二项分布问题当超几何分布处理.本文从三个层面剖析易混误区.
易混点一 超几何分布与二项分布的概念理解不深不透
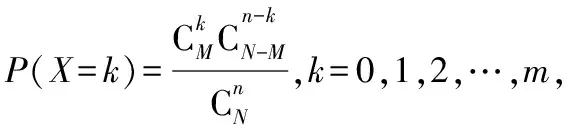
如果随机变量X的分布列具有下列形式:

X01…mPC0MCn-0N-MCnNC1MCn-1N-MCnN…CmMCn-mN-MCnN
则称随机变量X服从超几何分布.
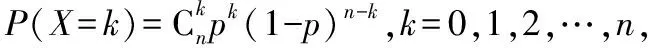
可见,超几何分布必须要知道总体的容量,且是不放回抽取;而二项分布不需要知道总体容量,且是放回抽取的.
易混点二 误把二项分布当超几何分布
例1在中国,不仅是购物,而且从共享单车到医院挂号再到公共缴费,日常生活中几乎全部领域都支持手机下单和支付.出门不带现金的人正在迅速增加.中国人民大学和法国调查公司益普索(lpsos)合作,调查了腾讯服务的 6 000 名用户,从中随机抽取了60名,统计他们出门随机携带的现金(单位:元)如茎叶图所示,规定:随身携带的现金在100及以上的为“淡定族”,其他为“非淡定族”.
用样本估计总体,若从腾讯服务的用户中随机抽取 3人,设这3人中“淡定族”的人数为随机变量ξ,求随机变量ξ的概率分布列及数学期望.

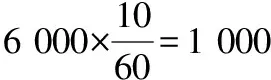
依题意得ξ=0,1,2,3,



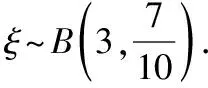

得随机变量ξ的分布列为

ξ0123P271 0001891 0004411 0003431 000

评析题目中已知“用样本估计总体”,这就是说要把样本的频率视为总体的概率进行计算,显而易见不是超几何分布问题,而是典型的独立重复试验,因而是二项分布问题.但学生很容易忽视“用样本估计总体”或不理解“用样本估计总体”,而用超几何分布求概率,错误地把样本容量6 000当成总体容量6 000,陷入以偏概全的解题误区.
例2为了尽快提高学生的数学成绩,某学校把试卷进行讲评后,再重新让学生测试,不出现任何的问题才“过关”,出现错误的同学认为“不过关”,根据分层抽样随机抽取50名学生,可得频率分布表如下:

分数段[0,60)[60,75)[75,90)[90,105)[105,120)[120,150]人数510151055过关人数125534
根据上表的信息,从高三的学生中选取5名,求至少 3名学生过关的概率.
错解依题意,抽取的50名学生中过关的学生共 7人,不过关的学生共43人,
则选取的5名学生中至少3名过关的概率为
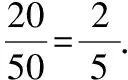
评析题目中要求“从高三学生中选取5人”,可高三学生总人数题目并没有告知,也就是不知道总体容量,这也正是超几何分布与二项分布的本质差别之一.因为超几何分布需要知道总体的容量,而二项分布不需要知道.因而学生很容易误把样本容量当成总体容量进行计算,陷入概念混淆,内涵与外延理解不透引起的解题误区.
例3近年来城市“共享单车”的投放在我国各地迅猛发展,“共享单车”为人们出行提供了便利.M市现有某种共享单车,某调查机构对这种共享单车的质量进行了调查,从使用过这种共享单车的市民中随机抽取了1 000人,每人分别对这种共享单车进行评分,满分均为60分,并将分数分成6组,得到频数分布表如下:

分数[0,10)[10,20)[20,30)[30,40)[40,50)[50,60]评分人数203050150400350
用样本估计总体,从参与调查的市民中任选4人,记其中对该种共享单车评分不低于30分的人数为X,求X的分布列与数学期望.
错解依题意,对该种共享单车评分不低于30分的共800人,评分低于30分的共200人.
依题意得X=0,1,2,3,4,


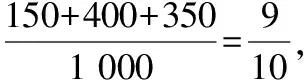


得随机变量X的分布列为

ξ01234P110 0003610 00048610 0002 91610 0006 56110 000
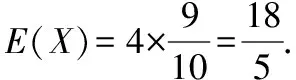
评析题目中给出“用样本估计总体”,这就说明基本事件的概率已知,显然不是超几何分布,而是重复试验,是二项分布问题.学生很容易忽视“用样本估计总体”,陷入概念理解不深不透引起的解题误区.
易混点三 误把超几何分布当二项分布
例42017年华北地区雾霾治理取得了很大成效,空气质量与2016年相比得到了很大改善.某市设有12个监测站点监测空气质量指数(AQI).如图是2017年11月的30天中,AQI的频率分布直方图,其中分段区间分别为[48,72),[72,96),[96,120),…,[216,240],11月仅有1天的AQI在[144,150)内.
(1)该市市民小孟是星期日查看官方公布的本市的AQI,如果AQI小于150,小孟就去体育馆踢球,以统计数据中的频率为概率,求小孟星期日去踢球的概率;
(2)“双创”活动中,验收小组把该市的空气质量作为一个评价指标,从当月的空气质量监测数据中抽取3天的数据进行评价,设抽取到的AQI不小于150的天数为X,求X的分布列与数学期望.


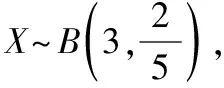
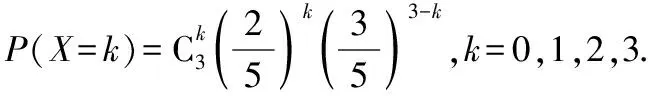
故X的分布列为

X0123P2712554125361258125


(2)依题意,得X=0,1,2,3,
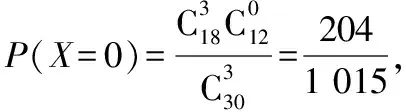
故X的分布列为

ξ0123P2041 0154591 0152971 01511203
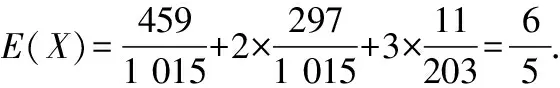
评析题目中已知“从当月的空气质量监测数据中抽取3天的数据进行评价”,这就说明是从30天中抽3天,显然是典型的超几何分布.但学生很容易看到频率分布直方图,产生错觉,就把频率当概率,看成二项分布的问题,陷入定势思维引起的解题误区.
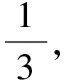

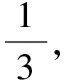


故ξ的分布列为

ξ0123P8271227627127
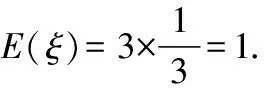
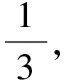
依题意得ξ=0,1,2,3,

故ξ的分布列为

ξ0123P145528551255155