加筋粗粒土筋土界面剪切特性与统计损伤软化模型研究
2018-12-06成浩王晅张家生宋良良
成浩,王晅, 2,张家生, 2,宋良良
加筋粗粒土筋土界面剪切特性与统计损伤软化模型研究
成浩1,王晅1, 2,张家生1, 2,宋良良3
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 中南大学 高速铁路建造技术国家工程实验室,湖南 长沙 410075;3. 中国中铁二院昆明勘察设计研究院有限责任公司,云南 昆明 650200)
土工合成材料与土的界面力学特性对于加筋土结构设计与稳定性分析具有重要意义。采用大型直剪试验研究不同法向应力下粗粒土与土工格栅界面的剪切特性。试验结果表明:筋土界面剪切应力与剪切位移曲线呈现出应变软化特征,加筋粗粒土较素粗粒土界面黏聚力增加,但内摩擦角降低;格栅的加筋作用明显减小了加筋粗粒土在峰值后强度的降低幅度,提高了土体的延性。基于统计损伤理论提出了考虑筋土界面应变软化特性的统计损伤本构模型,通过与试验结果进行对比分析,该模型能较好地反映筋土界面的应变软化特征,验证了模型的合理性。
加筋粗粒土;大型直剪试验;应变软化;统计损伤
土工合成材料在大型支挡结构、边坡、路基以及堤坝工程等工程中得到广泛应用,而筋土界面特性的研究是揭示土工合成材料加筋机理的关键环节,界面的相关力学参数也是进行加筋结构设计的重要指标[1]。目前进行加筋材料与土体界面摩擦特性研究的试验方法主要有拉拔试验和直剪试验,蔡剑韬[2]进行了不同竖向荷载下土工格栅加筋膨胀土的拉拔试验,认为其拔出过程可以分为界面静力摩擦阶段、渐进剪切阶段和整体运动阶段。Sidnei 等[3−5]采用拉拔试验研究了筋土界面的剪切特性,分析了格栅纵横肋对界面拉拔阻力的影响。王军等[6]采用大型直剪试验研究土工格栅与福建玻璃砂界面剪切特性,并定量分析了格栅横肋与纵肋对界面剪切强度的影响。王德银等[7]进行了不同纤维掺量加筋非饱和土的直剪试验,发现加筋土的剪切强度随纤维掺量的增加而增加。Makkar等[8−10]进行了不同条件下土工格栅与砂土的界面直剪试验,研究了筋材横肋、网孔形状及尺寸对界面剪切强度的影响。筋土界面的剪切特性主要是指界面剪切应力与剪切位移关系,许多学者提出了描述筋土界面剪切应力与剪切位移关系的非线性关系本构模型[11−13],然而土工合成材料与不同土体的直剪试验结果表明,筋土界面剪切应力与剪切位移关系曲线在达到峰值后会呈现出明显的应变软化,王军等[14]针对筋土界面的峰值后强度软化现象,提出采用双曲线模型和位移软化模型分别对曲线峰值前后进行模拟。Seo等[15]提出了基于扰动状态理论的筋土界面剪切软化本构模型。Anubhav等[16]基于砂土与土工织物的界面直剪试验结果,提出非线性双曲线模型对界面剪切软化曲线进行预测。但是上述模型大多是采用曲线拟合的方法对界面应力应变关系进行描述,模型参数的物理意义不明确。目前基于损伤力学与统计强度方法的统计损伤理论已广泛应用于岩土材料应力应变关系的模拟,且能较好地反映岩土材料的应变软化特性[17−8]。为此,本文通过室内大型直剪试验,研究粗粒土与土工格栅筋土界面剪切特性,在此基础上引入统计损伤理论建立能描述筋土界面剪切软化特性的统计损伤模型,并给出了模型参数的确定方法。最后采用试验结果对所提出的模型进行了验证。
1 试验设备与材料
1.1 试验设备
试验采用多功能大型界面直剪试验仪TAW-800,该直剪设备由上下剪切盒、液压动力系统、LVDT位移传感器、计算机控制系统及数据采集系统组成,可以实现单向剪切、循环剪切等复杂应力路径的剪切试验,上、下剪切盒尺寸长×宽×高为500 mm×500 mm×150 mm,试样竖向荷载通过刚性板施加,最大可达到800 kN,水平最大行程为300 mm,位移精度可达0.01 mm。仪器采用德国Doli公司的EDC全数字伺服控制器和数据采集软件,可对试验过程中的水平与竖向的剪切位移及荷载进行自动记录并保存。
1.2 试验材料
试验土样采用由黏土和级配碎石掺合而成的粗粒土填料,其中黏土颗粒含量为16.65%,碎石为颗粒呈棱角型的砾石类。根据TB10102—2010《铁路工程土工试验规程》,对其进行颗粒筛分试验后得到颗粒级配曲线如图1所示,土样的平均粒径约为0.52 mm;不均匀系数约为6.25,曲率系数约为1.44,其颗粒粒径分布均匀且级配良好。通过重型击实试验得到土样的最大干密度为2.23 g/cm3,最优含水率为6.5%。加筋材料选用工程中常用的经编涤纶双向土工格栅,筋材试样如图2所示,筋材的相关技术指标见表1。
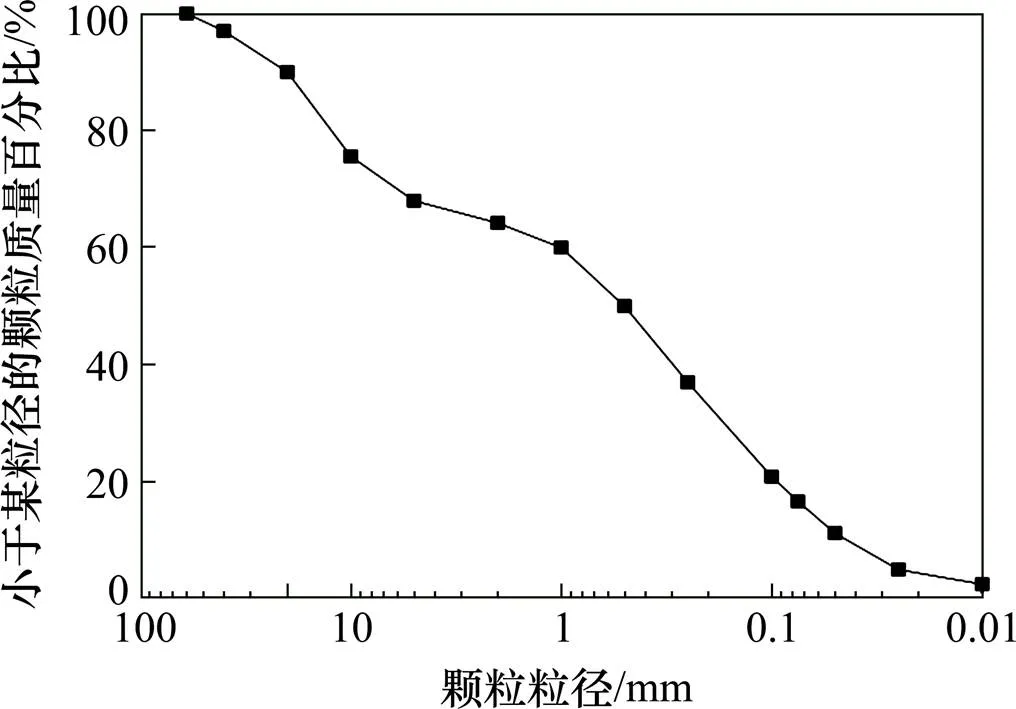
图1 粗粒土颗粒级配曲线

图2 试验用双向土工格栅
1.3 试验方案
为了研究双向土工格栅加筋粗粒土的效果,采用大型直剪仪分别进行粗粒土直剪试验和土工格栅与粗粒土筋土界面剪切试验。土工格栅的尺寸为520 mm×520 mm,筋材两端超出剪切盒部分通过夹具固定于下剪切盒。将粗粒土试样分3层装入剪切盒,并按压实度为90%的要求分层进行夯实、整平和刨毛,通过剪切盒内土样高度控制压实度。每组试样施加的法向应力分别为100,200和300 kPa,试验过程中剪切速率定为1 mm/min,剪切位移达到50 mm时结束试验。

表1 土工格栅技术指标
2 试验结果分析
图3和图4分别为不同法向应力下粗粒土和加筋粗粒土界面直剪试验曲线,由图可知,随着剪切位移的增大,剪切应力在达到峰值后均出现不同程度的软化过程;随着剪切位移的继续增大剪切应力逐渐趋于稳定值,即达到残余强度。不同法向应力下加筋粗粒土界面的剪切强度均低于素粗粒土内部的剪切强度,这是因为在剪切过程中土工格栅网格削弱了粗粒土颗粒之间的咬合作用。但是与素粗粒土相比,加筋粗粒土在峰值剪切应力后的软化现象明显得到改善,法向应力分别为100,200和300 kPa时,素粗粒土在峰值后的剪切强度分别下降了19.2%,12.4%和5.5%;而加筋粗粒土在峰值后的剪切强度分别下降了12.8%,6.2%和4.9%。这是因为剪切过程中土工格栅横肋由于受拉而对土体产生了被动阻力,随着剪切位移的逐渐增大,格栅横肋的加筋作用在进入剪切残余变形阶段后逐渐占主要作用,因此提高了筋土界面的残余强度。这也表明了土工格栅的加筋作用能有效提高土体的延性,并增大了筋土界面发生剪切破坏的可预见性。而法向应力越高,加筋对土体剪切软化的改善作用越不明显,这是由于在高法向应力下筋材与粗粒土颗粒之间相互作用更加紧密,筋材在剪切过程中可能发生磨损、断裂等破坏现象。图5给出了试验结束后不同法向应力下筋材的破坏情况,从图中可以看出,法向应力为100 kPa时土工格栅在剪切结束后还较为完整,而在法向应力为200 kPa时土工格栅已经发生扭曲,部分横肋和纵肋已经断裂,法向应力300 kPa下土工格栅的破坏已经十分明显,横肋和纵肋发生了明显的扭曲、断裂现象。
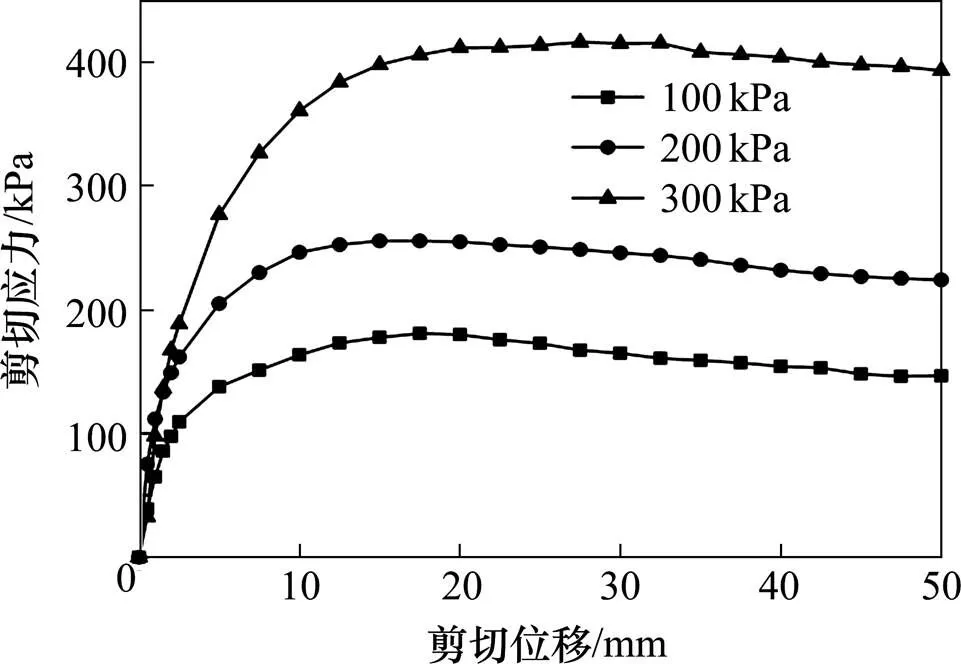
图3 不同法向应力下粗粒土剪切应力−剪切位移曲线

图4 不同法向应力下筋土界面剪切应力−剪切位移曲线

(a) σn=100 kPa;(b) σn=200 kPa;(c) σn=300 kPa
图6给出了加筋与未加筋条件下粗粒土剪切强度随法向应力的变化曲线,从图中可以看出,不同条件下剪切强度与法向应力均呈现良好的线性关系,对试验结果进行线性拟合便可得到粗粒土与加筋粗粒土的强度参数黏聚力和内摩擦角。粗粒土的黏聚力为50.7 kPa,内摩擦角为49.5°;而加筋粗粒土的黏聚力为54.9 kPa,内摩擦角为40.7°。土工格栅的加筋作用提高了土体的黏聚力,但是内摩擦角有所降低,这与Kim等[19]在进行加筋土直剪试验时得到的结论相一致。
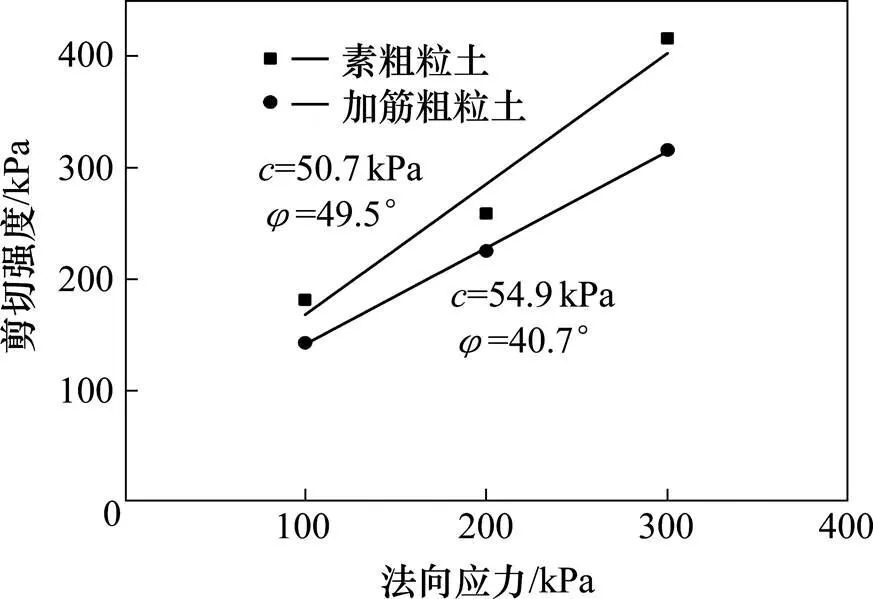
图6 界面剪切强度与法向应力关系曲线
3 筋土界面损伤软化统计本构模型
为了建立能够合理描述筋土界面剪切软化特征的本构模型,本文尝试引入目前在岩土工程领域中应用较为广泛的统计损伤理论,对筋土界面剪切变形的全过程进行模拟。其基本思路是将荷载作用下的筋土界面假定为由损伤和未损伤两部分组成,如图7所示,其中:为剪切面面积,为未损伤部分面积,为损伤部分面积。将剪切过程中损伤变量定义为损伤部分面积与剪切面面积之比, 则有:


根据筋土界面的受力平衡关系,可得:

式中:为筋土界面名义剪切应力;′为未损伤部分承担的剪切应力;″为损伤部分所承担的剪切应力;损伤变量表示了筋土界面在剪切过程中的损伤程度,且0≤≤1。将式(1)和式(2)代入式(3)中,可得如下应力关系式:


图7 剪切面单元微观应力分析
对于未损伤部分材料,认为其服从线弹性应力应变关系,即:
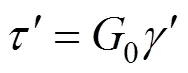
式中:0为初始剪切模量;′为未损伤材料的剪应变。根据Lemaitre应变等价性假设,剪切面名义剪应变与未损伤材料的剪应变′有如下关系;

由于一般直剪试验得到的是剪切应力与剪切位移的关系曲线,无法直接得到剪切应力与剪应变之间的关系曲线,因此本文中将剪切位移与试样在剪切方向上的尺寸的比值定义为剪应变[19],以得到剪切应力与剪应变的关系曲线。
传统的损伤模型认为材料的损伤部分不能承担任何荷载,因此当材料完全损伤(=1)后,其损伤部分承担的剪应力″为0,即界面的残余强度为零。但这与上述试验结果明显不符,从图5和图6中可以看出,剪切面的剪切强度在达到峰值后会出现一定的强度下降,随着剪切位移的继续增加逐渐趋于稳定值即达到残余强度。本文参考文献[18]所提出的方法,在损伤模型中考虑界面残余强度的影响,认为损伤部分材料仍能提供一定的剪应力,即″=,则改进后的筋土界面损伤模型为;

为了建立筋土界面的损伤演化模型,参考文献[17]的思路,假定损伤变量是关于剪应变的函数,并采用两参数的Weibull分布函数来描述剪切面的损伤演化规律,即;

式中:和0为Weibull分布函数的形状参数和尺度参数,由式(7)和式(8)即可得到考虑界面残余强度影响筋土界面损伤软化统计本构模型。

4 模型参数的确定方法
本文建立的筋土界面统计损伤本构模型有0,,0和4个参数,各参数均有明确的物理意义,其中0为初始剪切模量,为界面残余强度,而参数0和为损伤变量的演化参数。残余强度可由筋土界面剪切应力与剪切位移曲线确定,初始剪切模量0由式(10)确定,实际计算中可近似取为剪切应力−剪切位移曲线初始线性部分的斜率。

参考文献[17]中的分析方法,根据界面剪切应力−剪应变曲线的特性来确定参数0和的取值。由图3~4可知,筋土界面的剪切应力与剪切位移曲线具有明显的应变软化特性,因此曲线必然存在一个峰值点,当达到峰值点时,剪切应力达到峰值,且该点应力增量为0,即;
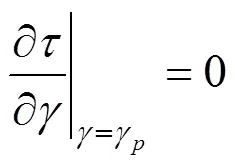

式中:为峰值剪切应力;为与峰值剪切应力对应的剪应变,由式(11)和式(12)即可得到参数0和的计算公式;


5 模型验证及讨论
根据直剪试验得到不同法向应力下的剪切应力与剪应变曲线,并对试验结果曲线进行数据处理,得到模型参数见表2。将表2中模型参数代入式(9),得到本文提出的统计损伤模型的计算结果。并将模型计算结果与试验曲线进行对比,结果如图8所示。从图中可以看出,模型计算结果与试验曲线较为吻合,能较好地反映剪切过程中的应变软化特性。图9给出了不同法向应力下损伤变量随剪应变的演化规律,从图9可以看出,随着变形的不断发展,损伤变量不断增大,当达到残余强度时,损伤变量也逐渐趋近于1。

表2 不同法向应力下损伤模型参数
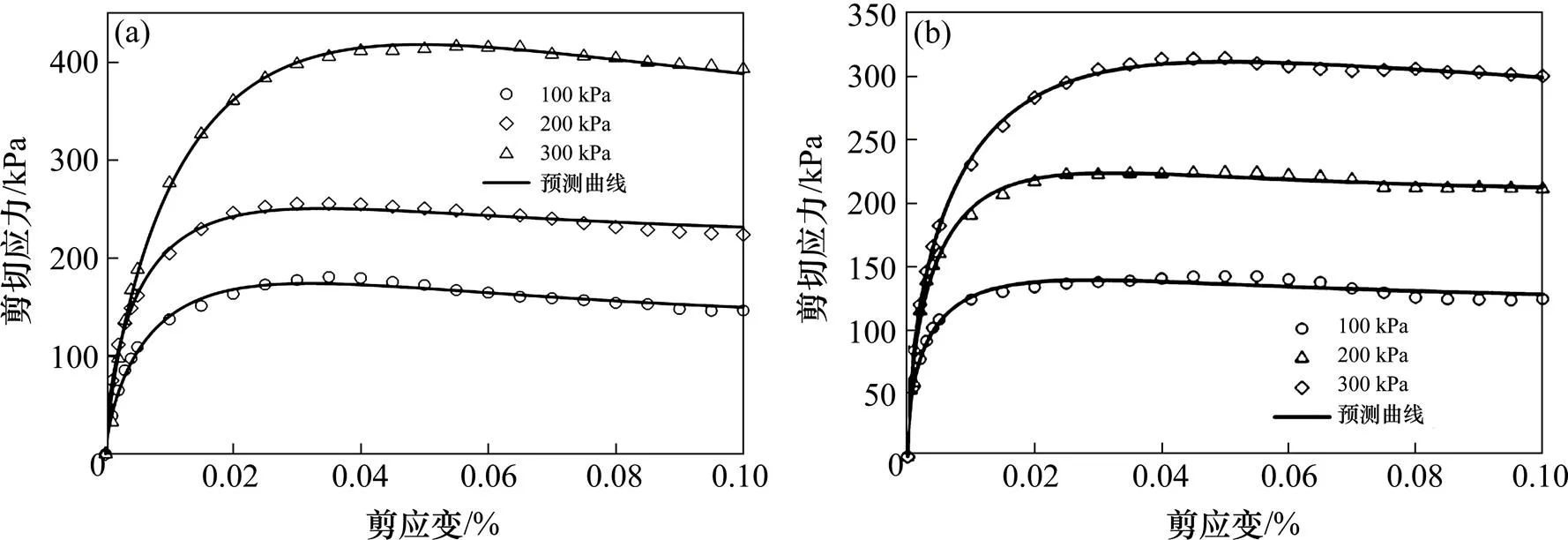
(a) 粗粒土;(b) 加筋粗粒土
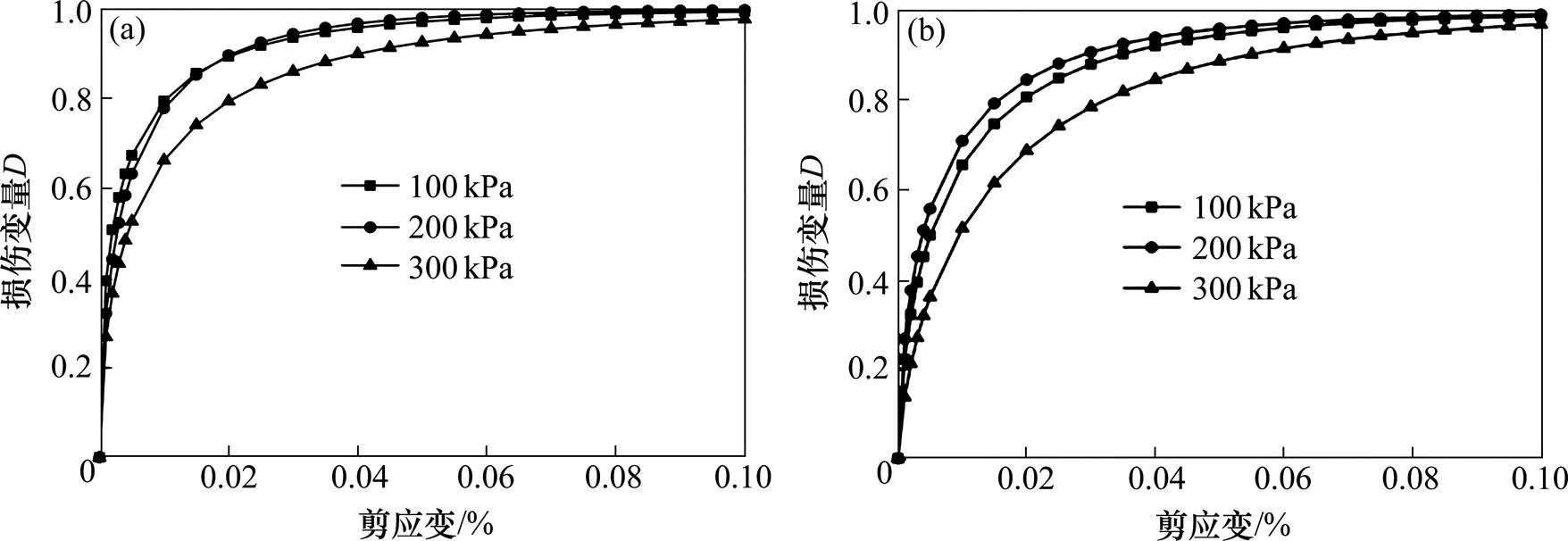
(a) 粗粒土;(b) 加筋粗粒土
6 结论
1) 筋土界面的抗剪强度随法向应力的增大而增大,剪切应力与剪切位移曲线在达到峰值后出现应变软化现象。格栅的加筋作用能明显减小加筋粗粒土在峰值后强度的下降幅度,提高土体的延性。
2) 抗剪强度指标表明,土工格栅的加筋作用能提高土体的黏聚力,但内摩擦角有所降低。
3) 基于统计损伤理论建立了能够合理描述筋土界面应变软化特征的统计损伤本构模型,模型同时考虑了残余强度的影响,能较好的对筋土界面剪切变形全过程进行模拟。通过与直剪试验结果进行对比分析,进一步验证了该模型的合理性。
[1] 李广信. 关于土工合成材料加筋设计的若干问题[J]. 岩土工程学报, 2013, 35(4): 605−610. LI Guangxin. Some problems in design of geosynthetic- reinforced soil structures[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(4): 605−610.
[2] 蔡剑韬. 土工格栅加筋膨胀土拉拔试验研究[J]. 岩土力学, 2015, 36(增1): 204−208. CAI Jiantao. Pull-out test on interface behavior between expansive soils and geogrids[J]. Rock and Soil Mechanics, 2015, 36(Suppl 1): 204-208.
[3] Sidnei H C T, Benedito S B, Jorge G Z. Pullout resistance of individual longitudinal and transverse geogrid ribs[J]. Journal of Geotechnical and Geoenvironment Engineering, 2007, 133(1): 37−50.
[4] 徐超, 廖星樾. 土工格栅与砂土相互作用机制的拉拔试验研究[J]. 岩土力学, 2011, 32(2): 423−428. XU Chao, LIAO Xingyue. Researches on interaction mechanism between geogrid and sand by pull-out tests[J]. Rock and Soil Mechanics, 2011, 32(2): 423−428.
[5] Palmeira E M. Bearing force mobilisation in pullout tests on geogrids[J]. Geotextiles and Geomembranes, 2004, 22(6): 481−509.
[6] 王军, 林旭, 刘飞禹, 等. 砂土与格栅界面相互作用的直剪试验研究[J]. 岩土力学, 2014, 35(增1): 113−120. WANG Jun, LIN Xu, LIU Feiyu, et al. Research on interaction of geogrid and sand interface by direct shear tests[J]. Rock and Soil Mechanics, 2014, 35(Suppl 1): 113−120.
[7] 王德银, 唐朝生, 李建, 等. 纤维加筋非饱和黏性土的剪切强度特性[J]. 岩土工程学报, 2013, 35(10): 1933− 1940. WANG Deyin, TANG Chaosheng, LI Jian, et al. Shear strength characteristics of fiber-reinforced unsaturated cohesive soils[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1933−1940.
[8] Makkar F M, Chandrakaran S, Sankar N. Performance of 3-D geogrid-reinforced sand under direct shear mode[J]. International Journal of Geotechnical Engineering, 2017(1): 1−9.
[9] LIU C N, Zornberg J G, CHEN T C, et al. Behavior of geogrid-sand interface in direct shear mode[J]. Journal of Geotechnical and Geoenvironment Engineering, 2009, 135(12): 1863−1871.
[10] 王家全, 周岳富, 唐咸远, 等. 可视大模型加筋土直剪数采仪的研发与应用[J]. 岩土力学, 2017, 38(5): 1533− 1540. WANG Jiaquan, ZHOU Yuefu, TANG Xianyuan, et al. Development and application of large size direct shear test apparatus with visual and digital collection functions for reinforced soil[J]. Rock and Soil Mechanics, 2017, 38(5): 1533−1540.
[11] 张诚成, 朱鸿鹄, 唐朝生, 等. 纤维加筋土界面渐进破坏模型[J]. 浙江大学学报(工学版), 2015, 49(10): 1952− 1959. ZHANG Chengcheng, ZHU Honghu, TANG Chaosheng, et al. Modeling of progressive interface failure of fiber reinforced soil[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(10): 1952−1959.
[12] 王磊, 朱斌, 李俊超, 等. 一种纤维加筋土的两相本构模型[J]. 岩土工程学报, 2014, 36(7): 1326−1333. WANG Lei, ZHU Bin, LI Junchao, et al. Two-phase constitutive model for fiber-reinforced soil[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(7): 1326− 1333.
[13] Esterhuizen J J B, Filz G M, Duncan J M. Constitutive behavior of geosynthetic interfaces[J]. Journal of Geotechnical and Geoenvironment Engineering, 2001, 127(10): 834−840.
[14] 王军, 林旭, 符洪涛. 砂土−格栅筋土界面特性的本构模型研究[J]. 岩土力学, 2014, 35(增2): 75−84. WANG Jun, LIN Xu, FU Hongtao. Study of constitutive model of sand-geogrid interface behavior in geogrid/ geotextile reinforced soil[J]. Rock and Soil Mechanics, 2014, 35(Suppl 2): 75−84.
[15] Seo M W, Park I J, Park J B. Development of displacement-softening model for interface shear behavior between geosynthetics[J]. Soils and Foundation, 2004, 44(6): 27−38.
[16] Anubhav, Basudhar P K. Modeling of soil–woven geotextile interface behavior from direct shear test results[J]. Geotextiles and Geomembranes, 2010, 28(4): 403−408.
[17] 曹文贵, 赵明华, 刘成学. 基于Weibull分布的岩石损伤软化模型及其修正方法研究[J]. 岩石力学与工程学报, 2004, 23(19): 3226−3231. CAO Wengui, ZHAO Minghua, LIU Chengxue. Study on the model and its modifying method for rock softening and damage based on Weibull random distribution[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3226−3231.
[18] 曹文贵, 赵衡, 李翔, 等. 基于残余强度变形阶段特征的岩石变形全过程统计损伤模拟方法[J]. 土木工程学报, 2012, 45(6): 139−145. CAO Wengui, ZHAO Heng, LI Xiang, et al. A statistical damage simulation method for rock full deformation process with consideration of the deformation characteristics of residual strength phase[J]. China Civil Engineering Journal, 2012, 45(6): 139−145.
[19] Kim D, Ha S. Effects of particle size on the shear behavior of coarse grained soils reinforced with geogrid[J]. Materias, 2014, 7(2): 963−979.
Shear behavior of geogrid-soil interface and its statistical damage softening model
CHENG Hao1, 2, WANG Xuan1, 2, ZHANG Jiasheng1, 2, SONG Liangliang3
(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. National Engineering Laboratory for High-Speed Railway Construction, Central South University, Changsha 410075, China; 3. Kunming Survey, Design and Research Institute Co., Ltd. of CREEC, Kunming 650200, China)
The interface mechanical properties between geosynthetics and soil are of great significance for the design and stability analysis of reinforced soil structure. In this study, large direct shear tests were performed on coarse-grained soil with/without geogrid reinforcement under different normal stress. The test results show that interface shear stress-shear displacement curves are characterized as strain softening; Compared with the no-reinforced case, the case reinforced with geogrid have larger cohesion and lower friction angles. The reduction in shear strength after reaching max value is obviously diminished and the ductility of soil is enhanced due to geogrid reinforcement. Based on statistical damage theory, a new statistical damage constitutive model is proposed to describe the strain-softening characteristics of geogrid-soil interface. Furthermore, the proposed model is verified by experimental results.
reinforced coarse-grained soil; large direct shear test; strain-softening; statistical damage
10.19713/j.cnki.43−1423/u.2018.11.008
TU443
A
1672 − 7029(2018)11 − 2780 − 08
2017−09−18
湖南省自然科学基金资助项目(2017JJ2314);中南大学研究生创新项目(2016zzts077)
王晅(1977−),男,甘肃庆阳人,讲师,博士,从事岩土工程教学和研究工作;E−mail:dddebug@csu.edu.cn
(编辑 涂鹏)
