深度单峰梯形神经网络

单传辉

北京工业大学 信息学部 计算机学院，北京 100124

1 引言

人工神经网络是受到组成动物大脑的生物神经网络的启发而提出的一种模糊数学模型。基于神经网络的深度学习已成为人工智能的一项强大技术。自Hinton等人[1]提出之后，已经在图像处理、音频和自然语言处理等方面取得了巨大的成功[2-8]，极大地影响了学术界和工业界。同时，以卷积神经网络为代表的神经网络受到了极大的关注。影响现代深层学习模型成功的关键因素之一是使用非饱和激活函数（例如ReLU）来取代饱和激活函数（例如sigmoid和tanh）。

就目前的文献来看，Jun Han等人详细介绍了sigmoid激活函数的性质[9]，sigmoid激活函数具有软饱和性，符合生物神经元的生物特性。但是，梯度消失问题是sigmoid激活函数难以克服的。tanh激活函数也是一类具有软饱和性的激活函数。Xavier等人[10]还进一步分析了sigmoid和tanh的饱和现象及其特点。类似地，tanh激活函数在深层神经网络中也存在梯度消失问题。修正线性单元（Rectified Linear Unit，ReLU）激活函数是一种稀疏非饱和的激活函数，由Xavier等人提出[11]。ReLU激活函数是一种将正响应变为其本身并将负响应变为0的逐元线性函数，这不仅解决了梯度消失问题，还使得深度神经网络的收敛更快。然而，一旦梯度达到0，ReLU激活函数就会出现潜在的劣势，即线性单元无法被激活。针对这个问题，Maas等人[12]提出了泄漏修正线性单元（Leaky ReLU，LReLU）激活函数，将ReLU的负响应部分用线性函数代替。He等人[13]进一步将LReLU扩展到参数线性单元（Parametric Linear Unit，PLeLU）激活函数，PLeLU是一种可以学习参数的修正线性单元。Clevert等人[14]提出了指数线性单元（Exponential Linear Unit，ELU）激活函数。相对于修正线性单元类型的激活函数，ELU收敛更快，且更具有泛化性。可是，在这两种类型的激活函数之间还存在着表示空间的空隙，即对于激活函数的负响应部分，ReLU或PReLU能够表示线性函数但不能表示非线性函数，而ELU能表示非线性函数但不能表示线性函数。因此，Li等人[15]提出了多参数指数线性单元（Multiple Parametric Exponential Linear Unit，MPELU）激活函数，MPELU能够适当性地在修正线性单元和指数线性单元进行切换。为了能够既学习凸函数又学习非凸函数，Jin等人[16]提出了S形修正线性单元（S-shaped Rectified Linear Unit，SReLU），相对于其他激活函数，例如ReLU、LReLU和PReLU，SReLU取得了很大的提高。

神经生物学研究表明，所有神经细胞均有静息电位[17]，神经细胞产生的所有电信号均叠加于静息电位之上。神经细胞产生的电信号分为两大类。第一类是局部分级电位。动作电位（也称为神经活动）是第二类主要电信号。当刺激强度继续增大并超过另一个较大阈值后，动作电位的幅度不变增大。显然，ReLU、LReLU、PLeLU、ELU、SReLU和MPELU激活函数都不符合神经细胞的这种生物特性，不可否认，ReLU、LReLU、PLeLU、ELU、SReLU和MPELU激活函数都取得了很好的效果。另外，刺激强度应该还具有第三个更大阈值，当刺激强度超过这个阈值后，动作电位的幅度为0。例如，人类的听力是有范围的，当物体的震动强度超过20 000 Hz后，什么也听不见。ReLU、LReLU、PLeLU、ELU、SReLU和MPELU激活函数也不满足这一点。因此，从ReLU激活函数着手，探究激活函数的上界响应问题，通过给ReLU激活函数设定上界，结合生物神经元特性，提出了单峰梯形线性单元（Single-Peaked Trapezoid Linear Unit，SPTLU）激活函数。

2 相关工作

本文主要专注于深度神经网络的激活函数，因此，只回顾该领域的相关工作。关于激活函数最近的工作是修正线性单元（Rectified Linear Unit，ReLU）激活函数[11]，这是深度神经网络取得突破性进展的关键因素之一。ReLU激活函数对正输入不做任何改变，将负输入变为0。因此，避免了梯度消失问题，并增强了训练更深神经网络的能力，sigmoid和tanh激活函数不能做到这一点。泄漏修正线性单元（Leaky ReLU，LReLU）激活函数是将ReLU的负响应部分乘以一个斜坡系数、正响应部分不变而得来的[12]，这样就避免了ReLU中的0梯度问题。He等人[13]发现损失函数关于斜坡的值是可微的，提出通过SGD来优化斜坡的值，这种参数修正线性单元称为PReLU。实验表明PReLU比ReLU收敛更快，并能提高卷积神经网络的性能。为了同时学习凸函数和非凸函数，Jin等人[16]提出了S形修正线性单元（S-shaped Rectified Linear Unit，SReLU）激活函数，达到在凸函数与非凸函数之间的适当性切换。除了这些修正线性单元激活函数之外，Clevert等人[14]提出了新型的指数线性单元（Exponential Linear Unit，ELU）激活函数，ELU在负响应部分与sigmoid激活函数类似，在正响应部分与ReLU激活函数类似。实验证明ELU能够使梯度更接近单位自然梯度，加快学习速度，提高网络的性能。针对激活函数两种表示类型之间的盲区，Li等人[15]提出了多参数指数线性单元（MPELU）激活函数。MPELU激活函数可以在修正线性单元和指数线性单元激活函数之间进行选择，并在CIFAR10/100数据集上取得了最优的性能。

3 生物神经元的响应特点

神经生物学研究表明，所有神经细胞均有静息电位，即细胞内相对于细胞外液为负性（不到100 mV）[17]。神经细胞产生的所有电信号均叠加于静息电位之上。有些信号使细胞膜去极化，使静息电位减小；另一些使细胞膜超极化，使静息电位增大。神经细胞产生的电信号分为两大类。第一类是局部分级电位。这些电位由外界的物理刺激所产生，例如，照射在眼中光感受器上的光；使耳中毛细胞发生形变的声波；压迫皮肤感觉神经末梢的触刺激；在突触部位（神经细胞及其靶细胞间的接头）的活动。动作电位（也称为神经活动）是第二类主要电信号。当局部的分级电位达到足够大使细胞膜去极化超过某一临界水平（称为阈值）时，动作电位产生。动作电位一旦产生，便迅速地进行长距离传播。与局部的分级电位不同的是，发生在神经元中的动作电位，其幅度和时程是固定不变的，就像电码中的点一样。信号通过视网膜的传送过程可以归纳如下所示[17]：

光→光感受器中的局部分级信号→双机细胞中的分级信号→神经节细胞中的分级电位→神经节细胞中的动作电位→传至高级中枢

在上述过程中起重要作用的是动作电位。动作电位的一个重要特征是，它是一种触发产生的、再生性的全或无事件。来自双极细胞和无长突细胞的信号作用在神经节细胞上，倘若其效应足以使该细胞达到阈值，就会产生动作电位。动作电位一旦产生，其幅度和时程将不由刺激的振幅和时程所决定。更大的刺激电流并不产生更大的动作电位；更长的刺激过程也并不使动作电位延长。如图1所示，动作电位是一个幅度约0.1 V的短暂的电脉冲[18]。只有动作电位的全部序列完成后，另一个动作电位才能在同一位置引发。在每个动作电位之后，必然有一个安静期（不应期），通常持续几毫秒，在此期间不能引发第二个冲动，因此，动作电位可能达到的最大重复频率受限于不应期。强度由放电的频率来编码。一种更有效的视觉刺激产生一个更大的局部电位，其结果是神经节细胞的放电频率更高，如图2所示[19]。这一现象最初为Adrian所描述[20]，他发现，在皮肤的一条感觉神经中，动作电位的放电频率是刺激强度的一种度量。此外，Adrian还观察到，施加于皮肤的刺激越强，会有更多的感觉纤维被激活。因此，对于坐骨神经干，一根神经纤维在受到阈值以上刺激产生动作电位不随着刺激强度增大而增大，而坐骨神经干是由许多神经纤维组成的，在受到阈值以上刺激时，由于引起不同数目神经纤维产生动作电位，随着刺激强度增大，神经纤维产生动作电位的数目也越多，动作电位的幅度也就越大，当全部神经纤维都产生动作电位时，动作电位的幅度就不会增大了。故在一定范围内，坐骨神经干动作电位的幅度随着刺激强度增大而增大。ReLU、LReLU、PLeLU、ELU、SReLU和MPELU激活函数符合随着刺激强度的增加动作电位的幅度增大这一性质，但是它们不符合随着刺激强度的进一步增加达到足够大时动作电位的幅度不再变化这一性质。因此，ReLU、LReLU、PLeLU、ELU、SReLU和MPELU激活函数并不完全符合生物学性质，虽然ReLU、LReLU、PLeLU、ELU、SReLU和MPELU激活函数都取得了很好的效果。而且，神经元的频率带宽不是无限的，换句话说，生物体对外界的刺激不是无限响应、无限增加的。例如，人的听力范围是20～20 000 Hz；当光照强度特别亮时，人类的视觉根本什么都会看不到。因此，生物体对外界刺激的响应应该具有一个上界阈值，当超过这个上界阈值时，生物体便不再响应。但是，ReLU、LReLU、PLeLU、ELU、SReLU和MPELU激活函数在刺激强度继续增加时响应趋向于无穷大。因此，它们不满足生物学事实。

图1 动作电位示意图（经极化向细胞注入电流进行刺激，引起去极化反应；当去极化超过阈值时，引起全或无动作电位。在动作电位期间，神经元内部变正）

图2 视网膜神经节细胞中动作电位频率是强度的函数（经微电极通去极化电流，产生局部电位；电流越大，局部电位越大，放电频率越高）

4 单峰梯形线性单元

神经生物学研究表明随着外界物理刺激的逐步增大，达到激发动作电位阈值之后，动作电位随后被激发，单个动作电位的产生是全或者无的状态。而一片生物组织拥有一片神经细胞组织，对外界物理刺激的反应是随着刺激强度的增大，达到激发阈值时，开始有响应；而后随着刺激强度的继续增大，响应越来越强烈；最后，刺激强度继续增大，响应不变。之前关于激活函数的研究从来没有考虑到刺激强度的上界阈值问题。基于生物体对外界刺激的响应特点和现象，也为了了解ReLU激活函数上界阈值的效果，为LReLU、PLeLU、ELU、SReLU和MPELU等改进激活函数上界阈值问题的研究提供思路和参考，本文提出了具有上界阈值的单峰梯形线性单元（Single-Peaked Trapezoid Linear Unit，SPTLU）激活函数，它更符合生物神经元特性。SPTLU函数的定义为式（1）所示：

其中，常数γ＞β＞α＞0，可以根据需要确定，SPTLU函数的图像如图3所示。拥有SPTLU激活函数性质的神经元称为SPTLU神经元。

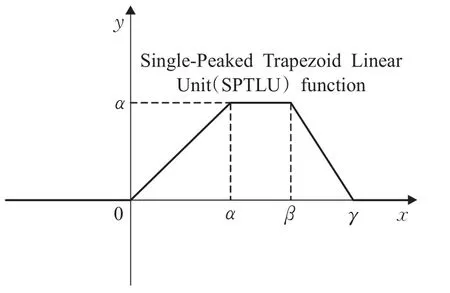
图3 SPTLU函数示意图

SPTLU神经元是在ReLU神经元的基础上，考虑生物对外界刺激拥有最大响应阈值而提出的。它符合生物神经元随着外界刺激低于响应阈值无响应，超过响应阈值响应逐渐增强，超过最大响应阈值后响应不变的特点。根据SPTLU神经元的数学定义（1），式（1）中的x=0点称为SPTLU神经元的响应阈值，式（1）中的 x=α点称为SPTLU神经元的最大响应阈值，式（1）中的x=β点称为SPTLU神经元的最大响应终止阈值，式（1）中的x=γ点称为SPTLU神经元的最大无响应阈值。

从数学上看，SPTLU激活函数是ReLU激活函数拥有上界响应的结果，从图3可以看出，SPTLU和ReLU激活函数负响应部分相同，正响应部分不同。SPTLU激活函数在正响应部分，随着外界刺激的增大，响应先是不断增大，接着不变，随后逐渐减小，最后为0不再变化，这与ReLU激活函数不同，ReLU激活函数在正响应部分，随着外界刺激的增大，响应一直随之增大。因此，通过设定ReLU激活函数的上界响应便可得到SPTLU激活函数。另外，需要注意的是，为了避免梯度消失问题，SPTLU激活函数在外界刺激达到最大响应终止阈值之后，SPTLU激活函数的响应依线性递减。

文献[11]指出ReLU激活函数相较于sigmoid和tanh激活函数更加具有稀疏性，即当x＜0时，ReLU激活函数的值为0，ReLU激活函数的有效部分全部集中在x＞0的部分。文献[11]进一步指出了ReLU函数稀疏性合理性及其好处。2001年，Attwell等人[21]基于大脑能量消耗的观察学习，推测神经元编码工作方式具有稀疏性和分布性。2003年Lennie等人[22]估测大脑同时被激活的神经元只有1%～4%，进一步表明神经元工作的稀疏性。从信号方面看，即神经元同时只对输入信号的小部分选择性响应，大量信号被刻意地屏蔽了。这样可以更好地提高学习的精度，更好更快地提取稀疏特征。从这个角度来看，传统的sigmoid函数同时近乎有一半的神经元被激活，这不符合神经科学的研究，而且此举也给深度网络训练带来巨大问题。ReLU激活函数满足了网络和神经科学对稀疏性的一定要求，而SPTLU激活函数比ReLU激活函数更加稀疏，当x＞γ之后SPTLU函数的值为0，比ReLU激活函数更加满足网络和神经科学对稀疏性的要求。

根据SPTLU激活函数的定义（1），其导数为：

从式（2）中可以看出，SPTLU激活函数的导数比较容易求解。激活函数的饱和性对网络的训练起着至关重要的影响，关系到训练过程中梯度是否合适，甚至梯度是否消失等问题。梯度消失问题是人工神经网络研究中很重要的问题，因此，激活函数饱和性的研究也备受关注。文献[23]对激活函数的饱和性定义为：在定义域内处处可导，且两侧导数逐渐趋近于0的激活函数 f()x（即定义为软饱和激活函数；与极限的定义类似，饱和激活函数分为左饱和激活函数和右饱和激活函数，左饱和激活函数定义为，右饱和激活函数定义为；与软饱和激活函数相对的是硬饱和激活函数，定义为当时，f′(x)=0，其中c为常数。根据这个定义，sigmoid和tanh激活函数都属于软饱和激活函数；ReLU激活函数是一类左侧硬饱和、右侧不饱和的激活函数，这也是ReLU激活函数获得突破性效果的原因所在；LReLU激活函数是一类左侧和右侧均不饱和的激活函数；SPTLU激活函数是一类左侧硬饱和、右侧硬饱和和中间不饱和的激活函数。在梯度消失问题上，SPTLU激活函数在不饱和区间内继承了ReLU激活函数的优点。

基于SPTLU激活函数可以构造各种各样的深层神经网络，称这些网络为深度SPTLU神经网络。比如，SPTLU与LeNet、LeNet7、VGG16和ResNet31结合产生SPTLU-LeNet、SPTLU-LeNet7、SPTLU-VGG16和SPTLU-ResNet31。下面通过对比实验分别检验这些网络的效果。

5 实验研究

本章利用LeNet、LeNet7、VGG16和ResNet31网络做了5组对比实验，每组实验数据都不同，这5个数据集分别为MNIST、Fashion-MNIST、SVHN、CALTECH101和CIFAR10，其中，MNIST和Fashion-MNIST数据集均利用LeNet进行训练。每组实验都有一个参照组和多个实验组构成，参照组是ReLU与上述网络结合产生的网络，分别为：ReLU-LeNet、ReLU-LeNet7、ReLU-VGG16和ReLU-ResNet31。参照组与实验组的不同之处只在于激活函数的不同，参照组的激活函数为ReLU激活函数，实验组的激活函数为SPTLU激活函数，网络其余设置均相同。另外，实验组包括SPTLU激活函数中不同参数α、β和γ的实验，对于不同的数据集，α、β和γ的取值不同，并给出多个不同α、β和γ的实验结果。所有实验组中，设定为2，即，因此，α、β和γ三者中只要其中两个参数确定，便可确定第三个参数。实验中，通过事先确定好α和β，然后计算出γ。下面介绍这些网络及其实验结果。

LeNet包含2个卷积层、2个池化层、2个全连接层和输出层，使用MNIST数据集。MNIST数据集拥有7万幅28×28的灰度图像，共分10类，由Yann LeCun和Corinna Cortes收集而来，其中包含6万幅训练图像，1万幅测试图像。SPTLU-LeNet与ReLU-LeNet对比实验结果如表1所示，该结果是在4×NVIDIA Tesla K40c上经过20遍训练后的结果。从表1中可以看出，ReLU-LeNet的准确率为99.30%，SPTLU-LeNet中的α、β和γ的取值为1.50-1.75-2.50、1.50-2.00-2.75、1.50-2.25-3.00、1.50-2.50-3.25和1.50-2.75-3.50，准确率均为99.30%。可以看出，SPTLU-LeNet准确率与ReLU-LeNet准确率相等，SPTLU达到与ReLU同等效果。

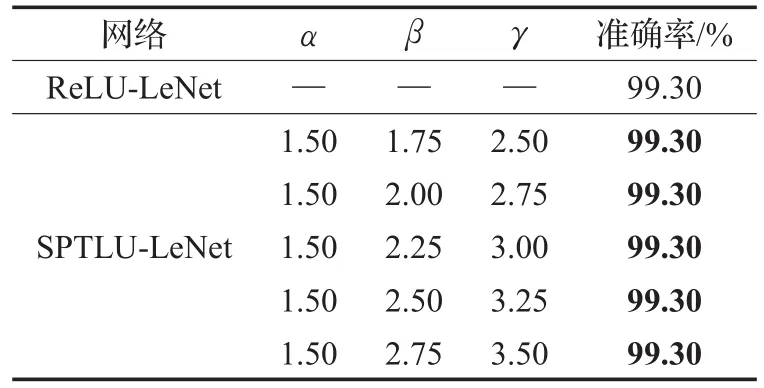
表1 SPTLU-LeNet与ReLU-LeNet的对比实验（MNIST）

Fashion-MNIST数据集拥有7万幅28×28的灰度图像，共分10类，由Zalando研究所的Han Xiao收集而来，其中包含6万幅训练图像，1万幅测试图像，Fashion-MNIST数据集的目的是将MNIST数据集替换为机器学习算法的良好检测器。SPTLU-LeNet与ReLU-LeNet对比实验结果如表2所示，该结果是在4×NVIDIA Tesla K40c上经过20遍训练后的结果。从表2中可以看出，ReLU-LeNet的准确率为91.90%，SPTLU-LeNet中的α、β 和 γ 的取值为1.50-1.75-2.50、1.50-2.00-2.75、1.50-2.25-3.00、1.50-2.50-3.25和1.50-2.75-3.50，准确率分别为91.90%、92.20%、91.90%、91.70%和91.80%。可以看出，α、β 和 γ在取值为1.50-1.75-2.50、1.50-2.00-2.75和1.50-2.25-3.00时准确率超过或与ReLU-LeNet准确率持平。特别地，在α、β和γ取值为1.50-2.00-2.75时准确率最高，为92.20%，SPTLU-LeNet比ReLU-LeNet准确率高出0.30%，SPTLU取得了比ReLU更好的效果。

LeNet7包含4个卷积层、4个池化层、2个全连接层和输出层，使用的数据集是SVHN数据集。SVHN数据集的训练集和测试集共有46 470幅32×32的彩色门牌号图像，共分10类，是来自谷歌街景视图（Google StreetView）的房屋数量，其中包含33 402幅训练图像，13 068幅测试图像。SVHN数据集还有验证集图像，这里没有使用。SPTLU-LeNet7和ReLU-LeNet7对比实验结果如表3所示，该结果是在4×NVIDIA Tesla K40c上经过10万步训练后的结果。从表3中可以看出，ReLU-LeNet7的准确率为89.91%，SPTLU-LeNet7中的α、β和γ的取值为5.00-5.50-8.00、6.00-6.50-9.50、7.00-8.25-11.75、8.00-8.50-12.50和9.00-10.25-15.25，准确率分别为89.78%、89.84%、90.05%、90.34%、90.22%和90.33%。可以看出，α、β 和 γ 的取值在7.00-8.25-11.75、8.00-8.50-12.50和9.00-10.25-15.25时准确率超过ReLU-LeNet7准确率。特别地，α、β和γ取值为8.00-8.50-12.50时准确率最高，为90.34%，SPTLU-LeNet7比ReLU-LeNet7高出0.43%，SPTLU取得了比ReLU更好的效果。

表2 SPTLU-LeNet与ReLU-LeNet的对比实验（Fashion-MNIST）

表3 SPTLU-LeNet7和ReLU-LeNet7的对比实验

VGG16包含13个卷积层、5个池化层、2个全连接层和输出层，使用的数据集是CALTECH101数据集。CALTECH101数据集拥有9 087幅大小不一的彩色图像，共分101类，由Lifeifei收集而来，其中包含7 579幅训练图像，1 508幅测试图像。SPTLU-AlexNet和ReLU-AlexNet对比实验结果如表4所示，该结果是在4×NVIDIA Tesla K40c上经过2万步训练后的结果。从表4中可以看出，ReLU-VGG16的准确率为52.00%，SPTLU-AlexNet中的α、β和γ的取值为3.00-3.25-4.75、4.00-4.24-6.25、5.00-5.25-7.75、5.00-5.50-8.00和 6.00-6.25-9.25，准确率分别为48.10%、50.80%、54.50%、52.70%和53.90%。可以看出，α、β和γ的取值在5.00-5.25-7.75、5.00-5.50-8.00和6.00-6.25-9.25时准确率超过ReLU-VGG16准确率。特别地，α、β和γ取值为5.00-5.25-7.75时准确率达到最高，为54.50%，SPTLU-VGG16比ReLU-VGG16高出2.50%，SPTLU取得了比ReLU更好的效果。

表4 SPTLU-VGG16和ReLU-VGG16的对比实验

ResNet31包含15个残差模块（每个模块2个卷积层）和输出层，共31层，使用的数据集是CIFAR10数据集。CIFAR10数据集拥有6万幅32×32的彩色图像，共分为10类，由Alex Krizhevsky，Vinod Nair和Geoffrey Hinton收集而来，其中包含5万幅训练图片，1万幅测试图片。SPTLU-ResNet31和ReLU-ResNet31的对比实验结果如表5所示，该结果是在4×NVIDIA Tesla K40c上经过8万步训练后的结果。从表5中可以看出，ReLUResNet31的准确率为92.00%，SPTLU-ResNet31中的α、β 和 γ 的取值为2.500-2.750-4.000、2.500-3.000-4.250、2.500-3.250-4.500、2.750-3.375-4.750和 2.750-3.875-5.250，准确率分别为94.00%、94.40%、92.00%、91.20%和91.20%。可以看出，α、β和γ的取值在2.500-2.750-4.000、2.500-3.000-4.250和2.500-3.250-4.500时准确率超过ReLU-VGG16准确率。特别地，α、β和γ取值为2.500-3.000-4.250时准确率达到最高，为94.40%，SPTLUResNet31比ReLU-ResNet31高出2.40%，SPTLU取得了比ReLU更好的效果。

表5 CIFAR10数据集ReLU和SPTLU激活函数的对照实验

注意：（1）从表1～5中可以看出，在α取值固定时，随着α和β二者之间差值的增大，基于SPTLU激活函数构成的网络的准确率先是随之增大，然后又随之下降，尤其表现在表2、3和5中。因此，α和β之间差值设定要适中。（2）从表1～5中可以看出，SPTLU激活函数在α、β和γ取值偏大时才取得与ReLU激活函数相当或者更优的效果，这与网络的卷积核的大小和网络有无使用局部响应归一化或者批归一化（Batch Normalization）有关。如果卷积核偏小，SPTLU激活函数达到与ReLU激活函数相当或者更优效果时的α、β和γ偏小，反之偏大。如果网络中使用了局部响应归一化或者批归一化，SPTLU激活函数达到与ReLU激活函数相当或者更优效果时的α、β和γ也偏小，反之偏大。

6 结束语

从理论上来说，SPTLU激活函数解决了现存的人工神经网络对刺激响应的无上界问题，并符合生物神经元的响应特性，修正了ReLU激活函数的无界响应问题和生物响应特性问题。从实验上来说，SPTLU激活函数也完全可以达到和超越ReLU激活函数的性能，且由SPTLU激活函数所引起的计算量和存储空间占用可以忽略不计（ReLU和SPTLU激活函数的本身计算复杂度都是O(1)（有限步内计算完成），在整个网络中二者的计算复杂度都是O(n)；SPTLU激活函数的空间复杂度相对于ReLU激活函数的空间复杂度，只在算法本身所占用的存储空间和运行过程中临时占用的存储空间略高，输入输出数据占用的存储空间均相同，二者本身的空间复杂度都是O(1)（有限参数存储），在整个网络中二者的计算复杂度都是O(n)。）。总之，SPTLU激活函数继承了ReLU激活函数的优点，比如稀疏性表示、选择性响应和一定程度上解决深层网络梯度消失问题，且符合生物神经元响应特性。同时，SPTLU激活函数比ReLU激活函数更加灵活，可以通过调整参数α、β和γ使得网络达到更好性能。可以说，SPTLU激活函数优于ReLU激活函数。当然，SPTLU激活函数也有一定的局限性，比如，SPTLU激活函数需要调整适当参数α、β和γ能够超越ReLU激活函数的性能。但是，这个适当的参数α、β和γ本文并没有给出具体公式进行求解，需要通过实验进行逐步尝试。对于这个问题也可以进一步研究。当然，本文意在介绍SPTLU这类带有上界阈值并符合生物神经元响应特性的激活函数。另外，本文的工作也为LReLU、PLeLU、ELU、SReLU和MPELU等改进激活函数上界阈值问题的研究提供思路和参考。