自适应动态邻域布谷鸟混合算法求解TSP问题
2018-12-04张红梅张向利
陈 雷,张红梅,张向利
桂林电子科技大学 广西高校云计算与复杂系统重点实验室,广西 桂林 541004
1 引言
旅行商问题(Traveling Salesman Problem,TSP)是经典的NP困难组合优化问题[1],该问题可描述为给定一组城市及城市之间的距离,求只经过每座城市一次并返回出发地的最短路线。TSP问题具有广泛的应用背景,如物流配送、航线设计等,是组合优化领域研究的热点。近年来,启发式算法已成为解决TSP问题的一种思路,如经典的遗传算法[2-3]、蚁群算法[4]、粒子群算法[5-7]和一些混合算法[8-9],以及新型群智能优化算法如蝙蝠算法[10-11]、帝国竞争算法[12]和布谷鸟搜索算法[13-17]等。这些算法为解决旅行商问题提供了优秀的方案。
布谷鸟搜索算法(Cuckoo Search,CS)是Yang于2009年提出的一种群智能优化算法[18],它通过结合列维飞行机制与偏好随机游走策略,在求解连续空间优化问题方面具有优良的性能[19]。同时也有一些学者将其改进并应用于求解组合优化问题,如TSP问题,其中Ouaarab等人设计了离散布谷鸟算法(Discrete Cuckoo Search Algorithm,DCS)[13]和基于随机键的布谷鸟算法(Random-Key Cuckoo Search,RKCS)[14],DCS 算法使用2-opt和双桥移动方式产生符合列维飞行机制的邻域,以此离散化布谷鸟算法,但DCS算法在遍历邻域时未进行筛选,且设置的步长概率是相同的,减缓了收敛速度,同时产生邻域的方式太过单一,不利于快速找到最优解;而RKCS算法引入了随机键表示法,利用列维飞行后的键值排序产生结果,但此方案不仅增加了额外的解码过程,也没有发挥列维飞行的特点,全随机排序增加了计算的复杂程度,降低了收敛效果。针对DCS算法的不足,张子成等人设计了一种自适应离散型布谷鸟算法(Adaptive Discrete Cuckoo Search,ADCS)[15],使用针对路径的自适应型局部调整算子和全局随机扰动策略,并引入2-opt优化算子来提升收敛速度,该方案相较DCS解的质量有了提升,但2-opt优化算子的运算时间复杂度为O(n3),若每一步都应用该优化算子,不仅会极大程度地拖延运算速度,而且该优化算子在大图中有时会破坏更优的解,导致无法收敛至全局最优解。林敏等人结合基于学习的混合邻域结构和概率接受准则,提出了混合离散布谷鸟(Hybrid Discrete Cuckoo Search,HDCS)算法[16],通过列维飞行选择相应的邻域结构进行寻优,并引入模拟退火算法的Metropolis接受准则,使算法不易陷入局部最优,一定程度上提升了解的质量,但该算法的学习规则是以当前最优解作为学习目标,而在迭代前中期向最优解的学习很难确保收敛,因此需要非常高的迭代次数才能获得优质的解。
因此本文针对上述问题,提出了一种自适应动态邻域布谷鸟混合算法(Adaptive Dynamic Neighborhood Hybrid Cuckoo Search,ADNHCS),首先对邻域结构进行了扩展,使之有可以产生更多富有变化的候选项;其次,设计了一种自适应概率调整策略,可动态调整离散列维飞行不同游走距离的概率,使之在不同迭代时期都具有优质的偏好步长;同时对于高效但耗时的2-opt优化算子采用dropout策略,保证快速收敛的同时避免大量无效计算;再次,为了提升邻域搜索效率,设计了一种圆限定突变的动态邻域结构来降低经典算法的随机性;最后,添加了禁忌搜索算法来扩展局部邻域搜索,提升了寻优效果,使用禁忌表和藐视准则防止重复搜索,降低陷入局部最优解的可能。实验结果表明,ADNHCS较其他基于布谷鸟搜索的算法和一些其他群智能算法,均可获得更接近全局最优解的优质解。
2 研究基础
2.1 旅行商问题的图论描述
图论中对于此问题的描述如下[9]:G=(V,E),其中V={v1,v2,…,vn}表示n个城市集(顶点集),E={eij|vi,vj∈V}是集合V中元素(城市)两两连接的边集,每一边都存在与之对应的权值。记城市V={v1,v2,…,vn}的一个访问顺序为T={t1,t2,…,ti,…,tn},ti∈V(i=1,2,…,n),且tn+1=t1,则其数学描述为:

其中eij表示城市i和城市 j之间的距离,xij表示该路径是否在旅行商的旅行路线中的一个决策变量,若旅行商选择此路径,则xij=1,否则,xij=0。即:
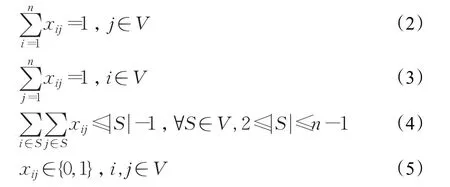
通过公式(2)~(5)可以确保该路径是一个合法的旅行商问题的解。
2.2 布谷鸟搜索算法
CS算法通过模拟布谷鸟的寄生育雏行为来有效地求解优化问题,它根据Levy飞行和偏好随机游走来获取全局最优解。Levy飞行是服从于Levy概率分布的,即寻优路径由频繁的短跳跃与偶然出现的长跳跃组成,这种寻优方式可以使CS算法拥有更大的搜索空间,更容易跳出局部最优[19]。另一方面,CS算法模拟了布谷鸟的繁殖行为,通过定义布谷鸟蛋被宿主鸟发现的概率,淘汰掉不适应环境的较差鸟蛋,孵化适应环境的优秀的鸟蛋,确保布谷鸟的群体都是由优秀个体组成,使得CS算法具有较强的收敛性[20]。在CS算法中假定遵循三条理想化的规则:
(1)每只布谷鸟每次只产一个卵,并随机选择一个鸟巢来孵化它。
(2)最好的鸟巢将被保留到下一代。
(3)布谷鸟可选择的鸟巢数量是一定的,鸟巢宿主发现外来鸟蛋的概率 pa∈[0,1]。
基于上述三条理想化规则的基础下布谷鸟寻窝的路径和位置更新如下:

基本CS算法的主要实现步骤为:
(1)初始化种群P,计算各个个体x的适应值 f(x)
(2)若未达到迭代终止条件,则重复执行:
(3) 对种群中的每一个个体x,重复执行:
(4) 使用Levy飞行生成新解y
(5) 若 f(y)<f(x),则用 y替代 x
(6) 按发现概率 pa丢弃差的解,使用偏好随机游动产生新解替代丢弃的解
(7) 记录全局最优解
(8)返回全局最优解
3 自适应动态邻域布谷鸟混合算法
在2.2节中介绍的CS算法主要用于解决连续优化问题,为了解决TSP等组合优化问题,要将连续型CS算法转换成离散型CS算法。
3.1 布谷鸟算法的离散化
3.1.1 适应度函数
TSP问题的目标是找到最短的周游路径,若用n个城市的访问次序x来表示问题的解,则适应度函数定义为:
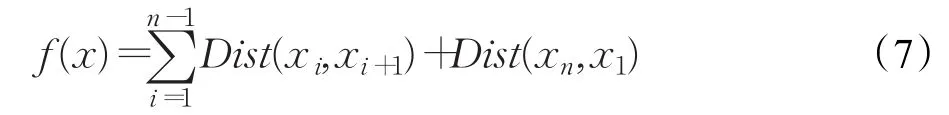
其中xi表示第i个被访问的城市,xi+1表示第i+1个被访问的城市,Dist(xi,xi+1)表示城市xi和城市xi+1之间的距离。
3.1.2 表示方式
每个鸟巢都表示TSP问题的一个解,设第i个鸟巢的解为 Xi=(Xi1,Xi2,…,Xin),其中 Xi1,Xi2,…,Xin代表n个城市的编号,表示从Xi1出发经过Xi2,Xi3,…,Xin等城市,最终返回出发点。
3.1.3 邻域结构
ADNHCS采用了可以切断2条边的反序算子(2-opt邻域)和可以切断4条边的双桥移动来产生候选集,为了丰富邻域结构,添加了具有多种变化形式的3-opt邻域结构。下面以8个城市的对称TSP为例,假设当前解为X=(1,2,3,4,5,6,7,8),介绍各种邻域结构及其生成的路径。
(1)2-opt邻域结构
又称为“反序算子”,选择两个城市并逆序其中的排列,一般情况下切断2条子路径会产生这样的效果,如切断2-3和7-8,逆序城市2和8之间的路径,得到候选项X1=(1,2,7,6,5,4,3,8)。
(2)3-opt邻域结构
即首先删除路径中的3条子路径,再尝试重新连接路径的所有其他可能形式,这个过程会产生3种新的路径,如图1所示,切断子路径1-2,3-4,5-6之后重组,可以得到3个候选项X1=(1,5,4,2,3,6,7,8)、X2=(1,3,2,5,4,6,7,8)、X3=(1,4,5,3,2,6,7,8)。

图1 3-opt邻域结构
(3)双桥邻域结构
是4-opt的一种特殊组成形式,如图2所示,切断子路径 1-2、3-4、5-6、7-8之后重组,得到候选项 X1=(1,6,7,4,5,2,3,8),由于此种移动形成的结构类似于两座桥,故称之为双桥移动,会对8个城市,4条子路径产生影响。

图2 双桥邻域结构
3.1.4 自适应概率调整策略
在上述提到的三种邻域结构基础上,根据邻域结构对解的扰动大小,将其划分为3种步长,通过Levy飞行的不同步长选择不同的邻域结构,短步长时采用扰动最小的2-opt邻域结构生成候选解集,长步长时则采用可以影响最多城市的双桥邻域结构生成候选解集,中距离步长则使用3-opt邻域结构生成候选解集。但由于在算法前期鸟巢中的每个解与最优解是有一定距离的,需要以较大幅度的扰动并结合2-opt优化算子来缩小每个解与最优解之间的距离,所以长步长在算法前期理应获得最大的概率,然而到了算法后期,优质的解都被保留了下来,鸟巢中的解只需微调就能达到最优解,因此算法后期要以短步长为主。综上所述,步长概率取值随算法迭代次数的增加而动态调整,是一个需要自适应的参数,经大量实验验证按照20%,30%,50%的区间概率设定可以达到较好的一个全局优化效果,故设定其概率定义式如下:

其中it为剩余迭代次数,tot为迭代总次数,P2-opt表示2-opt邻域产生的概率,Pdouble-bridge表示双桥邻域产生的概率,P3-opt表示3-opt邻域产生的概率。
3.1.5 Dropout策略
2-opt优化算子是一种用于解决TSP问题的路径局部优化算法[15],它依次交换路径中不相邻的两条边得到所有路径的集合,保留可以改善路径的交换。其时间复杂度高达O(n3),但又可以提供优质的快速收敛效果,因此在算法早期启动可以获得最大收益,而算法后期的解已经相对稳定,对每个候选项都启用该算子不仅浪费计算力还很难获得更优解。经大量测试发现设定算法早期dropout启动率为50%,中期和后期启动率为20%可以在运算时间和求解全局最优解方面实现最优策略,因此dropout概率定义式如下:

式中it表示剩余迭代次数,tot为迭代总次数,Pdropout表示2-opt优化算子启动概率,上式可将启动概率限定为从50%到20%的递减。
3.1.6 鸟巢被发现后的处理
若鸟巢被发现,则启用向最优鸟巢学习的策略,即选定被发现鸟巢的一个城市,在最优解中截取该城市后面一组城市,将其移至被发现鸟巢对应城市后面。假设选定的城市是3,最优解给出的城市3后的城市段为6,7和2,则调整之后的路径为X1=(1,3,6,7,2,4,5,8)。若该组城市路径已存在于被发现鸟巢之中,则使用双桥邻域算子对最优解的路径进行全局的扰动并用2-opt优化扰动后的路径,计算新路径的适应度,若比原路径适应度小则替换原路径,若比原路径适应度大则丢弃。若当前路径适应度小于全局最优解的适应度,则以当前路径为全局最优解。
3.2 动态邻域结构
为了降低在迭代后期随机选边带来的劣质候选集,ADNHCS对于2-opt邻域和3-opt邻域设置了一种圆限定突变的动态邻域结构来降低经典算法的随机性。以2-opt为例,图3(a)表示原路径,图3(b)表示随机移动后的路径,可见b1+b2-a1-a2是一个远大于0的数字,尽管这样的解也可以作为候选集,但其被选择为当前最优解的概率几乎为0,将在迭代后期增加许多不必要的搜索时间。

图3 2-opt随机移动造成路程增加
因此本文设计了一种动态邻域结构,可以在迭代后期减少无效的长距离路径交换,将2-opt邻域和3-opt邻域的候选范围减小到一个近邻域范围内。首先在城市集之中随机选择一个城市,然后根据半径r的选定规则确定范围内的点,得到点集之后,随机选择点集中的某些点构成的边来组成2-opt或者3-opt切边的候选集。半径r的选定规则如下,其中totallen表示路程总长度,citynum表示城市数:

以图4的邻域选择与2-opt交换为例,图4(a)表示原路径,图4(b)中随机选择了点8作为圆心,设置r为平均路径的两倍,以此选定的城市集合有{2,3,4,5,6,7,8,9},随机选择点集中的边(2,3)和(8,9),如图4(c)所示,将其切断并交换路径,可得到如图4(d)中所示的结果。
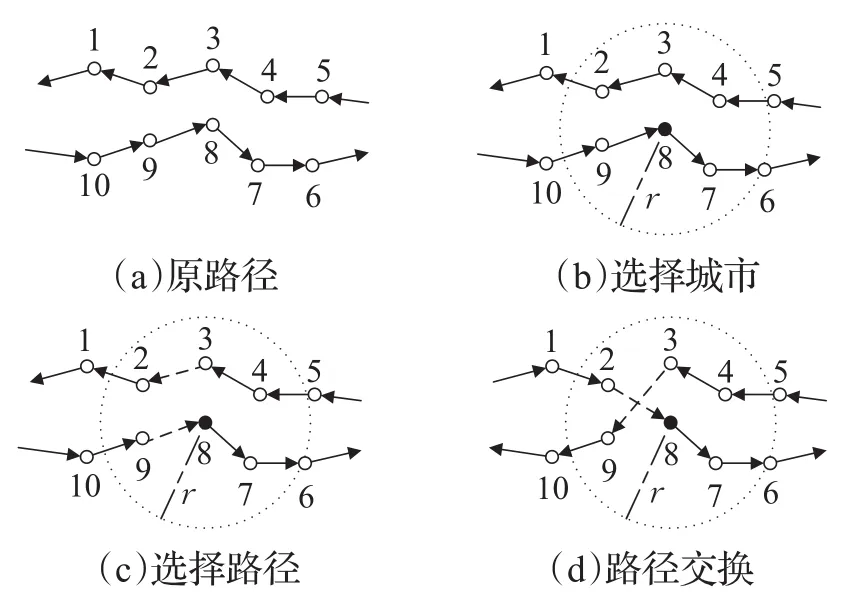
图4 邻域选择与2-opt交换
3.3 禁忌搜索的结合
禁忌搜索在ADNHCS之中的作用有两个,其一为扩展局部邻域搜索,通过Levy飞行产生基于当前鸟巢解的候选集;其二是根据禁忌表和藐视准则在候选集内选出最适用于当前鸟巢的解,补充了跳出局部最优解的手段。具体步骤如下所述,其中Sbest代表当前全局最优解,Snest表示当前鸟巢的解,tabulist表示禁忌表:
(1)采用Levy飞行生成候选集X并使用Dropout策略对候选集X执行2-opt优化,得到候选集Y
(2)计算候选集Y中各候选项的适应度,并按适应度 f(Yi)升序排列
(3)若 f(Y1)<f(Sbest),则 Sbest=Snest=Y1,并将Y1加入禁忌表,终止禁忌搜索
(4) 若候选集之中还有候选项,则重复执行:
(5) 若 f(Yi)≥f(Snest),终止禁忌搜索
(6) 若Yi∈tabulist,i=i+1,返回(3),否则Snest=Yi,并将Yi加入禁忌表,终止禁忌搜索
3.4 算法描述
综合3.1~3.3节的步骤与结论,ADNHCS的执行的主要流程如下:
(1)设定种群数目 pop,鸟巢被发现的概率 pa,迭代次数gen,禁忌表长度=候选集数目candi
(2)随机产生初始解集S={S1,S2,…,Spop},并计算个体的适应度 f(Si),找出当前最优解Sbest
(3)当没有达到循环次数时,重复操作:
(4) 对于每个Si:
(5) Levy飞行产生候选集X={X1,X2,…,Xcandi}
(6) 对于候选集X使用禁忌搜索检查是否有全局最优解,是否优于当前解
(7) 随机生成概率rand,若rand>pa,鸟巢被发现,则向最优解学习,对最优解执行一次双桥移动作为当前解
(8)返回最优解Sbest
其中(5)提到的Levy飞行产生候选集的具体实现方式为:
(1)随机生成概率rand,判断rand落在 P2-opt、Pdouble-bridge、P3-opt其中一个区间
(2)If迭代期位于迭代前中期
(3) 依据所落区间执行各邻域结构的生成规则,产生候选集X={X1,X2,…,Xcandi}
(4)Else
(5) 2-opt,3-opt采用动态邻域结构执行各邻域结构的生成规则,双桥邻域不采用动态邻域结构产生候选集 X={X1,X2,…,Xcandi}
(6)返回生成的候选集X
4 实验结果
4.1 算例与参数设置
为了验证ADNHCS算法的性能,本文选取了TSPLIB测试集[21]的多个不同规模的常用算例,并将ADNHCS算法与其他基于CS算法、新型群智能优化算法和基于经典智能优化算法的混合算法进行比较。程序编写并执行于MATLAB 2017a,Win10 1703系统,CPU 3.60 GHz,16 GB内存。
4.2 对比分析
4.2.1 ADNHCS与DCS和ADCS算法的比较
基于CS的算法有DCS[13]、RKCS[14]、ADCS[15]、HDCS[16]等,由于RKCS的样本数目太少且均运行于小数据集,无法表现其完整性能,故尽管ADNHCS优于RKCS,在此处暂不予比较;而HDCS的迭代次数远高于其他基于CS的算法,将其与移至同样具有高迭代次数的经典智能优化算法部分进行比较。
为了方便ADNHCS与DCS和ADCS算法对比,三者设置相同的参数,均为鸟巢发现概率Pa=0.2,集群数pop=20,迭代次数gen=500。同时,禁忌表长度tabulen和候选集个数candi的设置都会影响算法全局寻优能力。若禁忌表长度和候选集个数设置较大,算法运行时间长,但可以获得高质量解;若设置较少的候选集个数和禁忌表长,不仅会降低Levy飞行获得优质解的可能性,还影响禁忌搜索跳出局部最优解的能力。经大量实验表明对于不同规模的算例,当tabulen=candi=20时算法运行效果可获得性能与寻优的平衡。比较结果列于表1中,ADNHCS对每个算例都独立执行30次。其中Instances表示算例名称,Opt表示算例的理论最优解,Best和Mean分别表示该算法的最优解和平均解,PDb和PDav分别表示最优解偏差和平均解偏差,计算公式分别为:

表1 ADNHCS算法与DCS和ADCS算法的比较

从表1可以看到,在城市数少于300的11个小规模问题上ADNHCS算法的优势已经展现,其平均PDav仅为0.001%,当城市数超过300时,ADNHCS算法的平均PDav明显优于ADCS和DCS算法,仅有0.82%,可见ADNHCS在各种规模TSP问题上均具有较大优势,当算例少于500城市时几乎总能找到最优解,对于少于700城市的算例,PDav可以始终保持在1%之内,只有对于城市数超过800的算例,受收敛次数影响,会出现大于1%小于2%的偏差,但平均解和最优解差距很小,表示算法稳定性较高,且寻优效果较好。
从算例角度分析,以lin318算例为例,ADNHCS仅为0.16%的平均偏差率 PDav,是DCS的1/6,ADCS的1/2;对于rat575算例,ADNHCS将PDb和PDav准确地限制在了0.52%和0.93%,最优解的偏差率接近DCS和ADCS的1/4,平均解偏差率也有DCS和ADCS的1/3;对于nrw1379算例,ADNHCS依然可以保持1.19%的PDb,接近DCS和ADCS的1/3。可见当算例城市数继续增加时,ADNHCS相比DCS和ADCS依然可以保持稳定的优越性。
4.2.2 ADNHCS与经典智能优化算法比较
本节ADNHCS算法将会与HDCS算法和两个基于经典智能优化算法的混合算法进行比较,分别是四点三线遗传算法(Four Vertices and Three Lines Genetic Algorithm,4V3LGA)[2]和基于圆周定向突变的动态邻域结构自适应混合模拟退火禁忌搜索算法(the Adaptive Hybrid Simulated Annealing-Tabu Search with a Dynamic neighborhood structure based on a Circle-directed Mutation,AHSATS-D-CM)[9]。表2给出了ADNHCS算法与HDCS、4V3LGA和AHSATS-D-CM算法的比较结果。
其中4V3LGA是一种改进型遗传算法,通过第一阶段的变异算子优化和第二阶段是四点三线优化,将汉密尔顿环分为多个四点三线的汉密尔顿路径,并寻找最优路径来达到优化的目的。AHSATS-D-CM算法是模拟退火与禁忌搜索算法结合的混合算法,并且为了提升邻域突变的效果,设计了一种基于圆周定向突变的动态邻域结构。
其中,HDCS和AHSATS-D-CM均为高迭代次数的算法。HDCS总的迭代次数不超过pop×gen×citynum,其中citynum为城市数,gen代表迭代次数,pop代表种群数,对于最简单的eil51算例,51个城市,2 000次迭代,30个种群,迭代次数就高达3.06×106,而这些迭代次数随着城市数目增多也会随之增加,AHSATS-D-CM也给出了2×106数量级的迭代次数,而ADNHCS的总迭代次数为 pop×candi×gen,其中candi为候选项个数,总迭代次数为2×105。尽管对于智能优化算法来说迭代次数越多,找到最优解的概率就越高,但从表3的结果来看,ADNHCS无论是在最优解还是在均值的求解中,都表现出了稳定的全局寻优效果,在17个算例中只有3个平均解没有达到理论最优解,平均PDav仅有0.029%,AHSATS-D-CM在算例超过140城市时开始出现与理论最优解的偏差,其平均PDav为0.1%,HDCS和4V3LGA分别只有1个和4个算例的平均解达到了理论最优解,平均PDav分别为0.19%和0.91%。

表2 ADNHCS算法与HDCS、4V3LGA和AHSATS-D-CM算法的比较
4.2.3 ADNHCS与新型群智能优化算法比较
为了进一步验证ADNHCS算法的性能,本小节选择了新型群智能优化算法-离散蝙蝠算法(Discrete Bat Algorithm,DBA)[10],参数设置与4.2.1小节相同,比较结果列于表3中,其中Worst表示该算法的最差解,C1%表示运行结果在最优解1%范围内解的个数,Copt表示运行结果是最优解的个数。
从表3中可以看到,无论是最优解、平均解、最差情况的值还是的比率,ADNHCS算法均优于DBA算法,经计算得知DBA的平均偏差率PDav为0.515%,而ADNHCS的PDav仅为0.185%。同时ADNHCS在少于400城市的算例中可以确保稳定的全局寻优,在25个算例中只有3个算例的均值没有达到理论最优解,而DBA仅有8个算例得到了理论最优解。
对于C1%的观察可以发现,对于城市数少于500的算例,ADNHCS可以将解的值限制在最优解1%的范围内,DBA则只能确保城市数少于200的算例解的值可以落入最优解1%范围内。同时ADNHCS在城市规模超过1 000算例解的才超出最优解1%范围,表明ADNHCS在较大规模算例的运算上面仍然具有稳定高效的收敛效果。
4.2.4 ADNHCS收敛效果图
为了证明ADNHCS算法在不同类型数据集的收敛效果,使用了4个属性各异的算例进行测试分析,分别为城市分布有规律的tsp225算例;城市分布高度规律和分散的ts225算例,以及城市分布高度集中且无规律的pr226算例和rat575算例。图5~8为对应的收敛曲线和路径图,从图中可见由于2-opt优化算子和dropout策略的引入,对于不同类型、不同规模的数据集,ADNHCS均可在前50次迭代中实现快速收敛,在求解TSP问题中展现出良好的搜索性能。

表3 ADNHCS算法与DBA算法的比较

图5 tsp225的最优路径图与收敛曲线
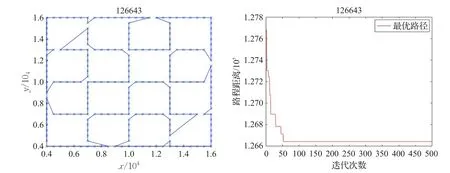
图6 ts225的最优路径图与收敛曲线

图7 pr226的最优路径图与收敛曲线

图8 rat575的路径图与收敛曲线
5 结束语
本文提出了一种用来求解TSP问题的ADNHCS算法,将离散CS算法与禁忌搜索方式结合,降低陷入局部最优解的可能,同时对邻域结构进行了扩展,可以产生更多富有变化的候选项,提高候选集的质量。而可动态调整离散列维飞行不同游走距离的概率的自适应概率调整策略的引入,增强了算法的全局搜索能力,为高效但耗时的2-opt优化算子使用dropout策略,平衡了快速收敛与无效计算力的矛盾,最后,圆限定突变的动态邻域结构避免了远距离的无效交换,提升了邻域搜索效率。在TSPLIB算例进行的实验结果也验证了ADNHCS算法相较其他基于CS的算法和部分新型或经典群智能算法,在求解TSP时有更好的收敛速度和收敛精度。
