基于加权Schatten-p范数和l2，1范数的鲁棒主成分分析

姜 伟，吕 倩，李 健

主成分分析（PCA）算法作为一种经典的去噪方法已经广泛应用在图像处理［1］、计算机视觉［2］等方面，PCA模型适用于去除密集的高斯小噪声，但是对于非高斯噪声或当某些位置的噪声极大时，PCA算法效果很不理想［3］.因此，Wright等人提出的鲁棒主成分分析［4-5］（RPCA）算法可以很好地解决这一问题.由于矩阵的秩是非凸不连续函数，RPCA优化的问题为一个NP-Hard问题，很难求解.因此，引入核范数鲁棒主成分分析［6］.该算法对原有模型矩阵的不同奇异值的惩罚力度相同，所求出的全局最优解在实际问题中效果差.为此本文提出一个新模型，即基于加权Schatten-p范数和l2，1范数的WLSRPCA模型.加权Schatten-p范数将分配到的不同的奇异值最小化，从而更准确的近似原始的低秩矩阵，l2，1范数则作为新的损失函数更高效地找到数据中的异常值或特征噪声［7］.此模型既能更好地估计秩的最小化，又能增强对异常值的鲁棒性，而且在图像去噪的应用上有较好的效果.

1 预备知识

定义1 对于任意矩阵X∈Rm×n，矩阵X的l2，1范数定义为.矩阵X的加权Schatten-p范数定义为tr(WΔp)，其中，0＜p＜1，W=[w1，w2，…，wr] ，r=min{m，n} ，并且wi≥0，i=1，2，…，r.W和Δ是对角矩阵，其中对角元素为wi和σi.

定理1 对于任意矩阵A∈Rm×n，若存在正交矩阵U∈Rm×n和V∈Rm×n，则矩阵A的奇异值分解为，其中对角 矩 阵 ΩA=diag(σ1，σ2，…，σr)，其 元 素 满 足σ1≥σ2≥…≥σr≥0.

引理 1［6］对于任意两个矩阵A∈Rm×n，B∈Rm×n分别进行奇异值分解，则有A=UΔVT和B=QΛRT，其 中 ，Δ=diag(σ，σ，…，σ) ，12rΛ =diag(b1，b2，…，br).则 (σ1，σ2，…，σr)是以下问题的解.

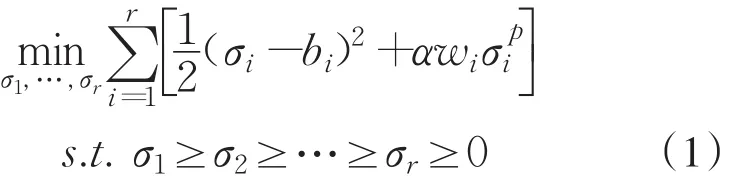
引理2［6］对于任意两个矩阵A∈Rm×n和B∈Rm×n，定义σ(A)=[σ1(A)，σ2(A)，…，σr(A)]T，σ(B)=[σ1(B)，σ2(B)，…，σr(B)]T. 其 中 ，σi(A) 和σi(B)分别是矩阵A和矩阵B的奇异值，r=min{m，n} ，有 tr(ATB)≤tr(σ(AT)σ(B)).

2 加权Schatten-p范数和l2，1范数的WLSRPCA

2.1 模型的建立

给定一个数据矩阵X∈Rm×n，核范数鲁棒主成分分析模型如式（2）所示.

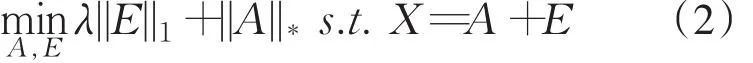
其目标就是将X分解成低秩矩阵A∈Rm×n和稀疏矩阵B∈Rm×n，即X=A+E（.2）式对所有奇异值都用同一值收缩，根据奇异值的先验知识，使不同奇异值对应不同的权值，我们将用加权Schatten-p范数代替核范数，用l2，1范数代替l1范数，将分配到不同奇异值的权重最小化.因此建立基于加权Schatten-p范数和l2，1范数的WLSRPCA模型，如（3）所示：

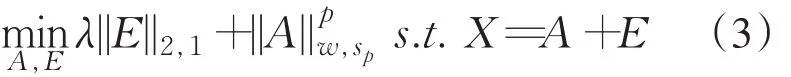
2.2 模型的求解

对（3）构建增广拉格朗日函数如下.

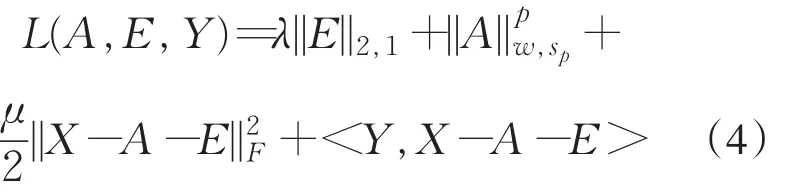
其中，矩阵Y为拉格朗日乘子并且惩罚系数μ＞0.使用交替方向法迭代更新矩阵A，E，Y和惩罚系数μ.求解目标函数的流程如表1所示.

表1 求解目标函数的流程

求解目标函数的详细流程如下.

固定矩阵E和矩阵Y，更新迭代矩阵A.删去（4）式中与矩阵A无关的量，优化（5）式问题：

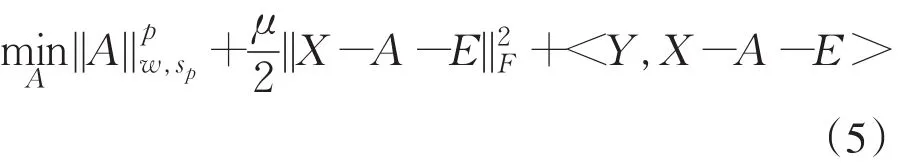
如果权重满足wr≥…≥w2≥w1≥0，由引理1可得的最优解为，其中，根据广义软阈值算法（GST）［5］可知=GST(bi，wi，p)，i=1，…，r，0＜p＜1.即解为

固定矩阵A和矩阵Y，更新迭代矩阵E.删去（4）式中与矩阵E无关的量，优化（6）式问题：

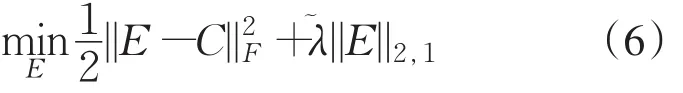
其中，C=X-A+μ-1Y，λ͂=λμ-1.

则根据文献［8］上式的解为：

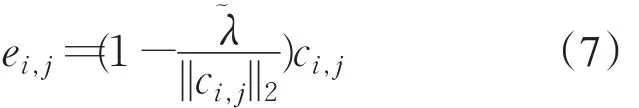
其中，（7）式为（6）式每一个优化子问题的最优解.则E*=Tλ͂(C).

固定矩阵A和矩阵E，更新迭代矩阵Y.则矩阵Y的迭代更新公式为Y=Y*+μ(X-A-E).其中，惩罚系数μ的迭代更新公式为μ=min(ρμ，μmax).

权值W的选取.W=[w1，w2，…，wr]的作用是使矩阵中较大的奇异值收缩幅度变小，较小的奇异值收缩幅度变大.因此其中的wi和σi(X)应为反比例关系.即c＞0为一个常数，θ＞0保为0时，权重仍可以计算.

以上为应用增广拉格朗日乘子法求解WLSRPCA模型的过程，具体算法步骤如表2所示.

表2 求解WLSRPCA模型的算法步骤

3 实验

实验将本模型与RPCA模型作比较，选取大小650×650，PSNR=62.9，结构化噪声为10%的图片，通过他们在图片恢复上的对比，也可以说是对矩阵恢复模型的精度的比较来检验效果如何.下面给出这两种模型在单张图片恢复上的效果，及在相同噪声的情况下两个模型去噪数据的比较，如图1和表3所示.

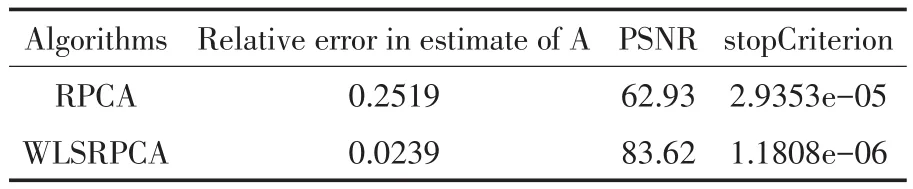
表3 去噪后数据对

4 结论

在初始条件相同的情况下，通过图1可以观察到，RPCA模型恢复出来的图片与原始数据有一定的差距.而本文所提出的模型对图片的恢复更接近于原始观测图像，即恢复的图片效果更好.通过表3数据显示，在相同噪声的情况下，本模型恢复的错误率更低于RPCA模型，且PSNR也远高于RPCA模型.因此，本文模型在图片恢复方面优于RPCA模型.实验结果证明本文所建模型的有效性及可行性，且算法是收敛的.关于本文WLSRPCA模型是否能够比RPCA模型更好地去除高斯、椒盐等噪声将是今后要关注的问题.