一类特殊四维交错代数上的Rota-Baxter算子

崔宝生

交错代数是一类很重要的非结合代数，与李代数［1］、约当代数及马尔策夫代数均有密切联系.Rota-Baxter算子最早出现在概率论中［2］.1960年，G.Baxter在研究Spitzer恒等式［3］时提出Rota-Baxter算子的概念.本文主要研究一类特殊四维交错代数上的Rota-Baxter算子和对应的八维交错代数上的交错杨-巴克斯特方程的张量形式的解.

1 一类特殊的四维交错代数上的Rota-Baxter算子

定理1 对于定理1当中第一类四维交错代数(A，∘)，它的Rota-Baxter算子在e0，e1，e2，e3下对应的矩阵为

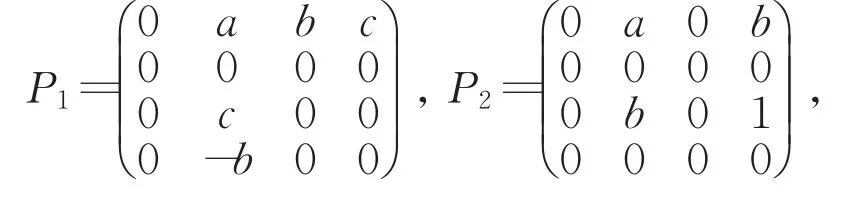
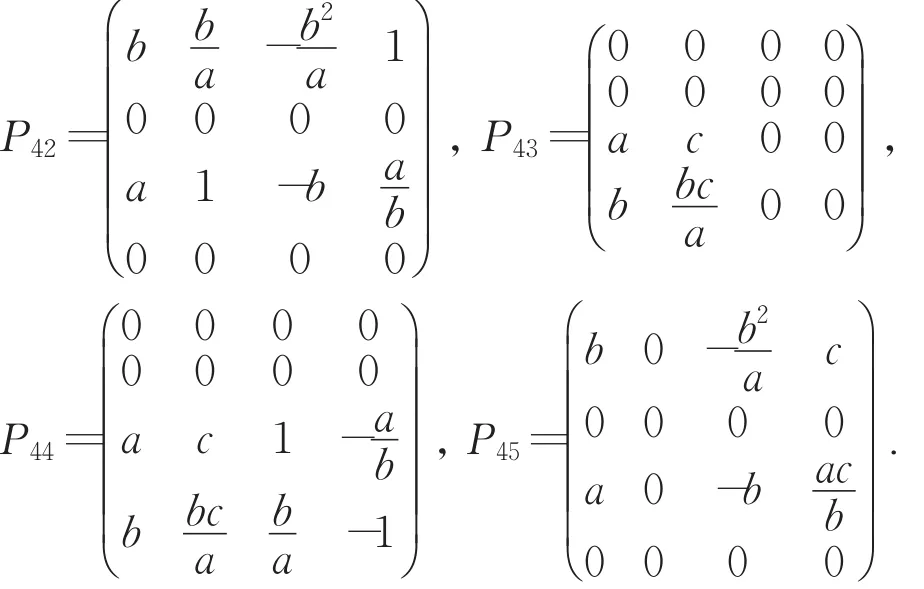
其中a，b，c，d≠0.

2 一类特殊八维交错代数上的交错杨-巴克斯特方程的解

定理2 定理1中第一类四维交错代数(A，∘)，(A，∘)上的Rota-Baxter算子Pi对应的上的交错杨-巴克斯特方程的解ri如下：

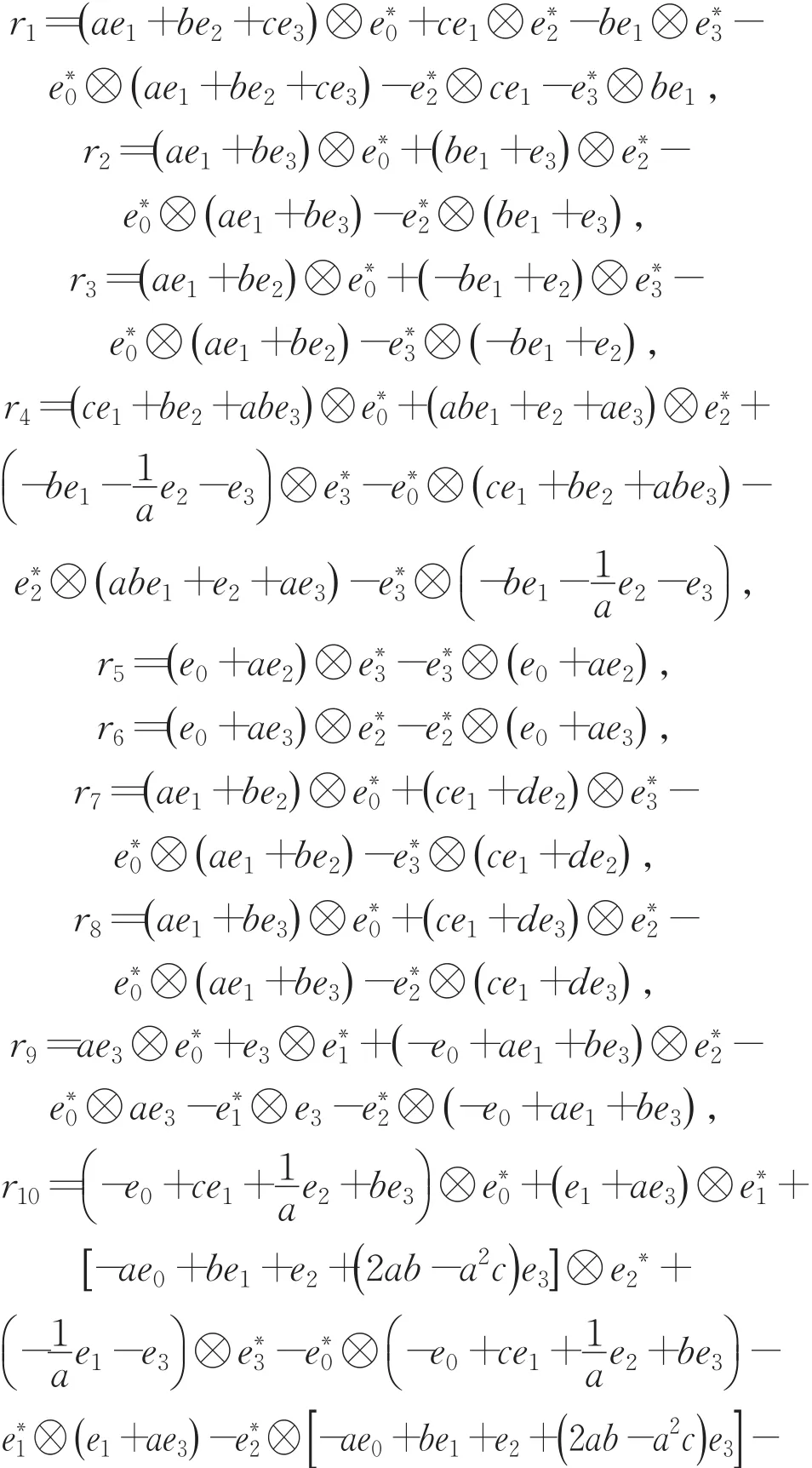
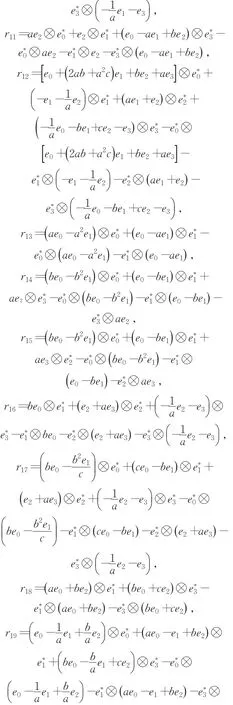
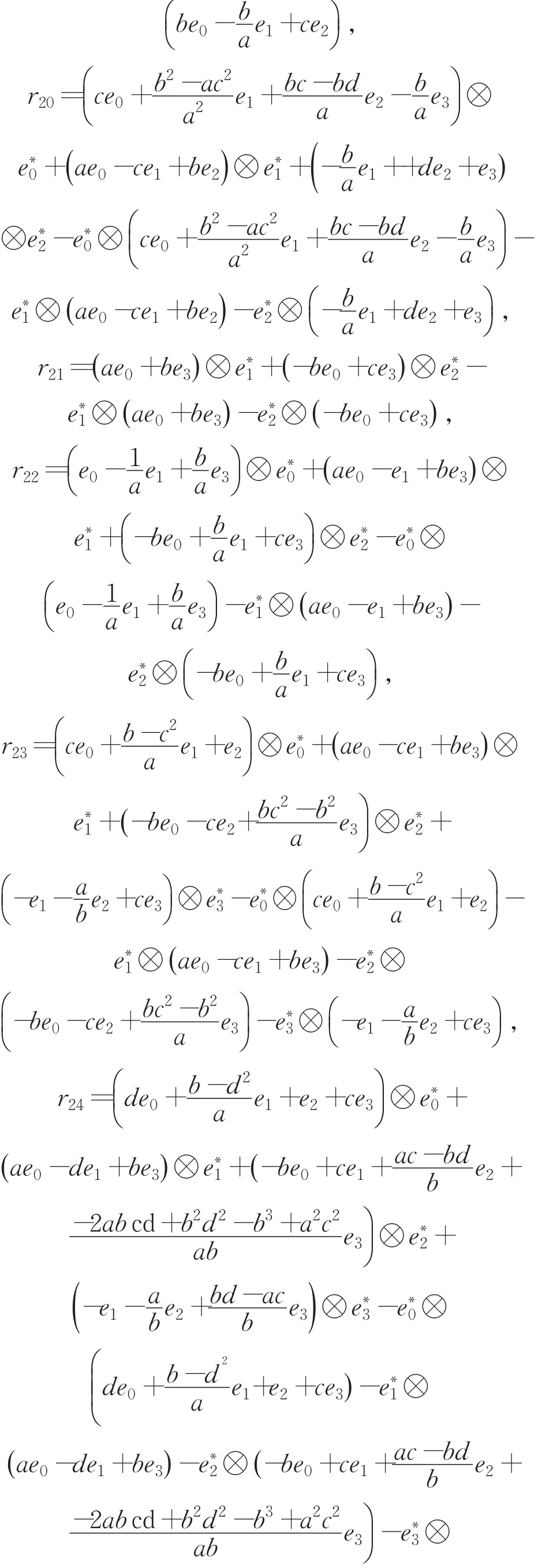
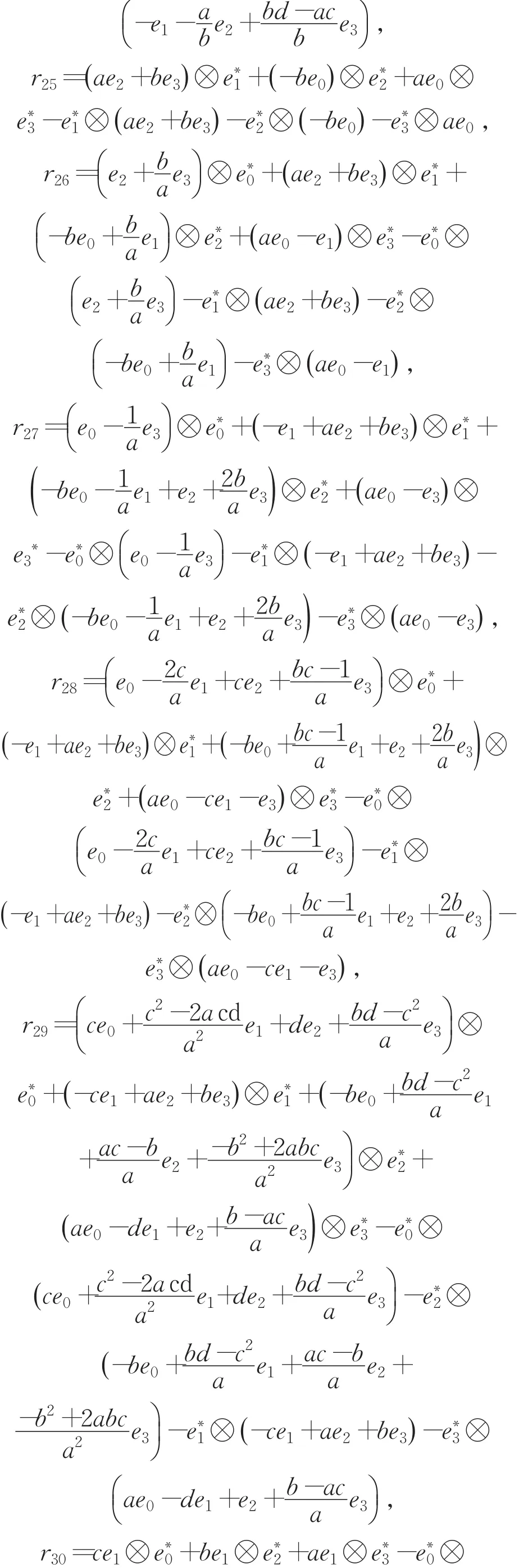
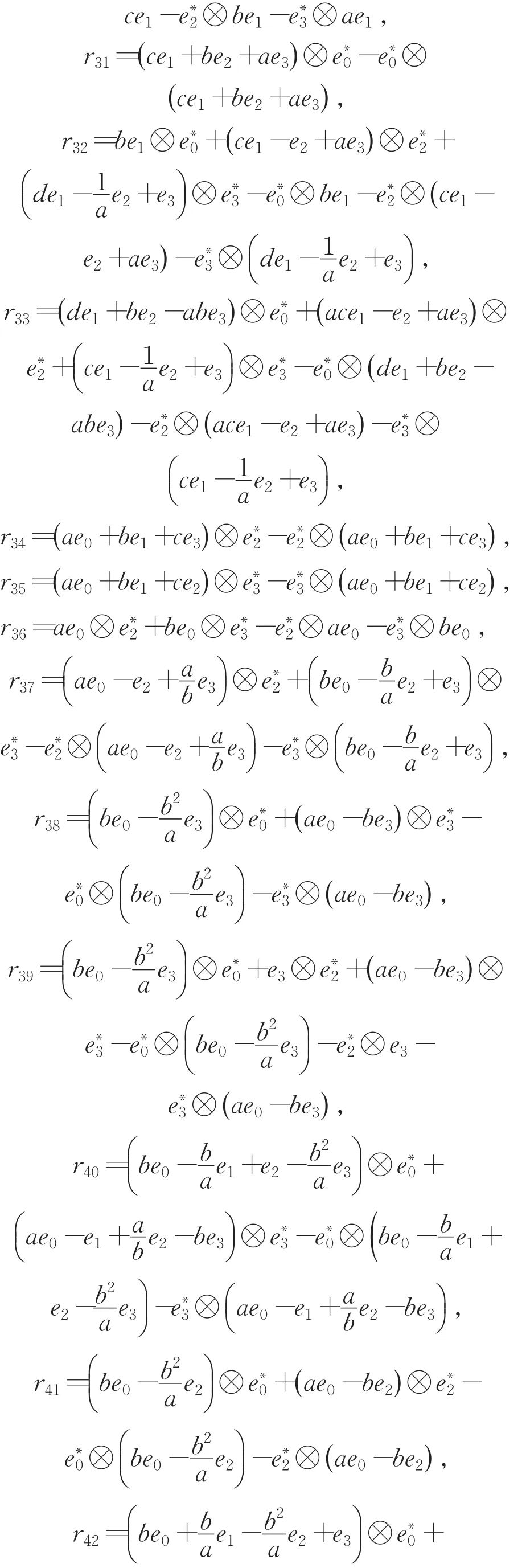
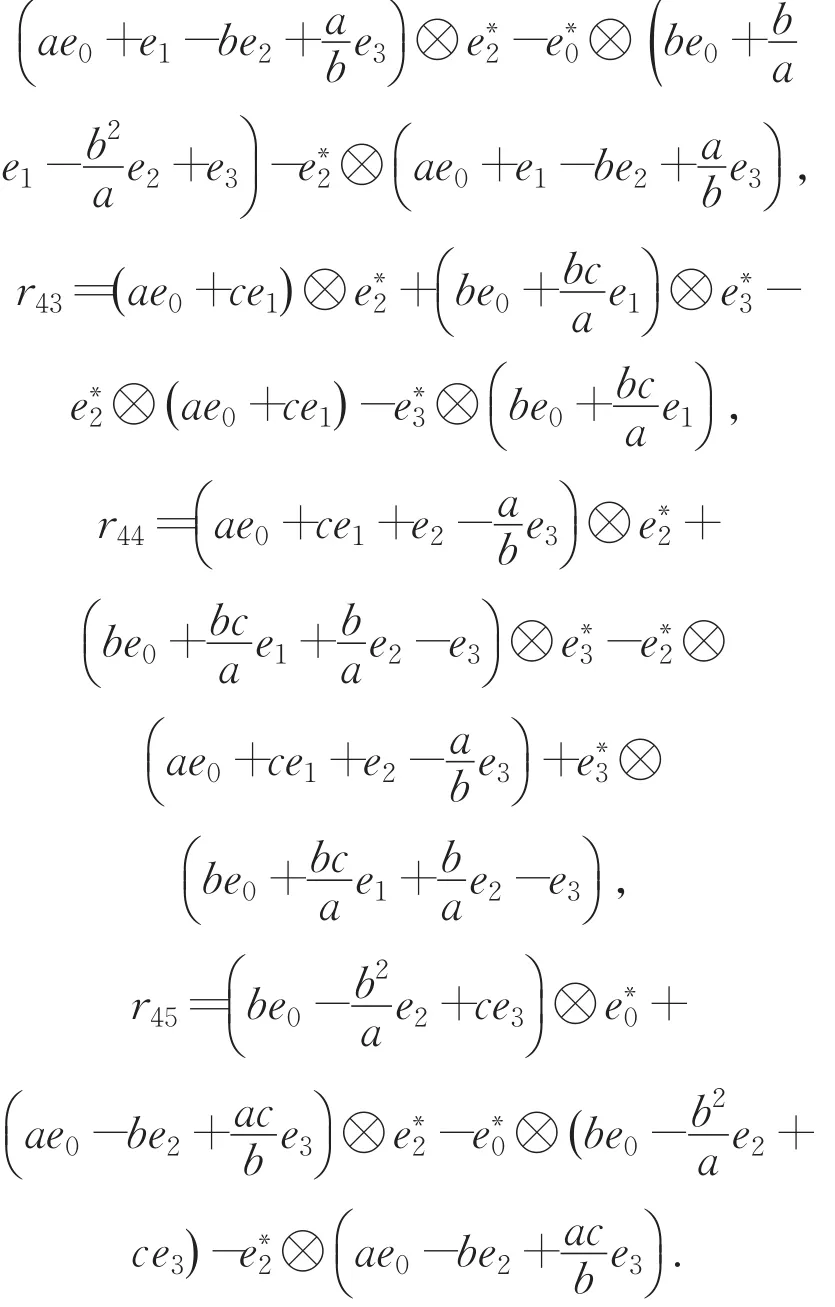
3 结论

本文主要利用交错代数上的Rota-Baxter算子的定义，通过计算得到第一类四维交错代数上的Rota-Baxter算子和对应的八维交错代数上的交错杨-巴克斯特方程的张量形式的解.因此，可以利用这种方法来计算第二类四维交错代数上的Rota-Baxter算子和对应的八维交错代数上的交错杨-巴克斯特方程的张量形式的解.同样可以得到类似的结果，可以进一步研究.