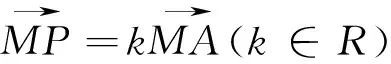一道竞赛题的解法分析与拓展探究

江苏省海门市能仁中学 (226100)

朱冬怡

2017年上海市初三数学竞赛第三题题目如下：

图1

如图1，在平面直角坐标系xoy中，直角三角形ABC的直角边AC=5,BC=4.锐角顶点A、B依次在x轴正半轴，y轴的正半轴上移动，则直角顶点C的轨迹的长度为 .

本题以几何图形的运动为载体，条件清晰明了，但由于轨迹不明，思考时需要运用动态思维、数形结合、逻辑推理与合情推理相结合的思想方法，具有很强探究价值.为此笔者从解法探究与结论推广两个角度对这个问题作了一定研究，现在将所得整理出来，与读者朋友分享.

1.解法分析

1.1 首先求出点C(x,y)的轨迹是什么图形

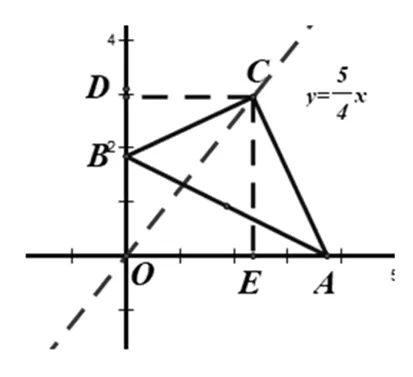
图2

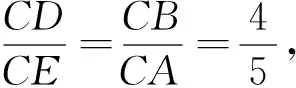
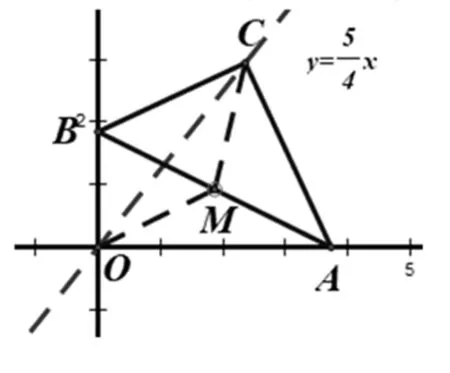
图3

设M(x0,y0)，则点

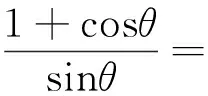
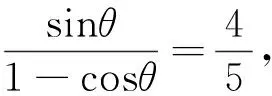
1.2 点C的轨迹长度为几何

C轨迹正好与四边形ACBO对角线CO所在直线重合，现在需要确定的是对角线CO长度的范围.如何确定？

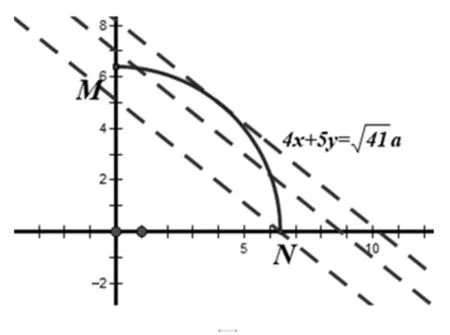
图4

思路3 (四点共圆)设OA=x(x≥0)，OB=y(y≥0)，OC=a(a>0)，由圆的内接四边形托勒密定理，

进一步的思考：更多点的轨迹问题.

2.问题拓展

在本题中，定长线段AB运动是旋转与平移两种运动的复合，运动过程中运动对象形状大小均保持不变，通过本题可以发现，运动图像中的点运动轨迹可能是线段，也可能是一段圆弧，那么其它点的运动轨迹又如何呢？