一道选择压轴题的命制和教学实践

福建省福清第三中学 (350315)

何文昌

2018年1月，笔者参加福州教育研究院组织的命题培训.培训结束前，每人需命制一道高考模拟卷选择题压轴题，每个小组选择一道题讨论并在培训班展示.笔者命制的一道题被小组长选中，经小组成员打磨后，由笔者进行展示.在1月份的校内月考中，高三年级备课组将该题呈现给学生.现将试题的命制历程及校内实测、课堂讲评情况展示出来，与同行们交流.

一、试题命制过程

(一)构思的背景

翻阅了近年高考真题中的第12题后，2015年新课标Ⅰ卷理12引起了笔者的兴趣.

设函数f(x)=ex(2x-1)-ax+a，其中a<1，若存在唯一的整数x0，使得f(x0)<0，则a的取值范围是( ).

图1

创新从模仿开始.把原题中的指数型换成对数型，保留过定点的直线方程y=ax-4a，再依托经典函数f(x)=clnx+dx2+ax+ab，初步的构思是利用函数f(x)=clnx+dx2-ax+4a进行命制.使用几何画板时(如图1)，用点C′和D′的纵坐标表示参数c和d，从而控制g(x)=clnx+dx2.移动点C′和D′，选取c=2和d=-1，确定了函数g(x)=2lnx-x2和f(x)=2lnx-x2-ax+4a，得到初稿如下：

设函数f(x)=2lnx-x2-ax+4a，其中a>0，若关于x的不等式f(x)≥0有唯一整数解，则a的取值范围是( ).

(C)(2-ln2,2] (D)(1,2)

(二)小组的讨论

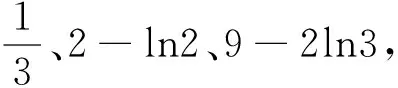
(定稿)设函数f(x)=2lnx-x2-ax+4a，其中a>0，若关于x的不等式f(x)≥0有唯一整数解，则a的取值范围是( ).

试题立意：本题考查学生对数学本质的理解，区分度恰当.本题通过把不等式转化为函数，隔离两个函数，利用导数确定函数的极值和单调性，从而求解参数的取值范围．本题考查导数在解决函数问题中的应用及直线的知识，考查化归与转化思想、函数与方程思想、数形结合思想，考查运算求解能力、推理论证能力、抽象概括能力．

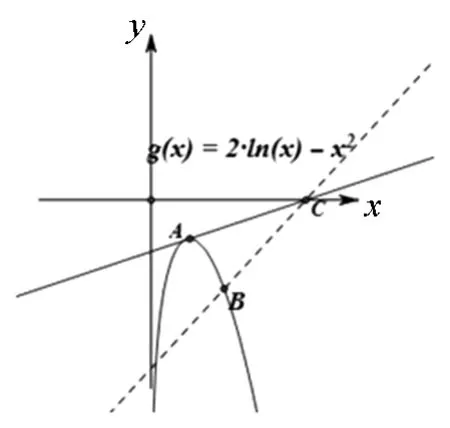
图2

成题后，大家进一步提出以下思考：

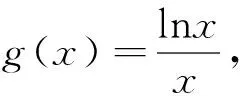
郭老师：改变直线所过的定点；

念老师：题中的解法对参数进行半分离，从而形成一直一曲的局面，这种小题巧做的思路和方法很有用.

(三)思维的碰撞

无独有偶，泉州市2018届高中毕业班1月单科质量检查(文科数学)第12题采用的思路和方法与小组讨论的内容几乎一样！题目(答案为A)如下：

设函数f(x)=lnx-ax2-(a-2)x，若不等式f(x)>0恰有两个整数解，则实数a的取值范围是( ).

命题工作是艰难的，当我们沉浸于其中时，往往会有许多想法，而一些想法是无效的,可一旦思路被打开后，那种思维流淌所带来的快乐是无与伦比的.在选择题的命制过程，笔者体会到以下两个方面：(1)题干要陈述完整、精炼、准确、包含选择支相同的内容；(2)选择支要与题干有关联、要独立、无暗示、能体现典型错误.

二、试题实测结果

在高三年级的1月份月考中，年级备课组把定稿作为数学试卷的选择题12题.阅卷完成后，经过统计，全班51位学生中有17位选出了正确答案，有14位学生选了A，有8位学生选了C，有15位学生选了D.

三、试题课堂讲评

本题正确率高达近33%，而且选A、D的学生也接近30%，这两点引起了笔者的注意.在课堂上，笔者带着疑问讲评了这个题目.

教师请一位做对的学生说出他的解题过程.

为了了解使用这种方法答对的学生人数，教师进行统计，共有8位学生.

教师请选择A的学生说出错误解法.

学生2：与学生1相同.

教师统计了使用这种方法的学生人数，共计25位.教师意识到多数学生在解题过程中遇到了困难.

教师：遇到求参数的取值范围时，一般用什么方法解决？

学生3：分类讨论或者分离参数法.

教师：分类讨论通常在大题压轴题中使用.小题要巧做，大家在使用分离参数法的过程中，遇到了什么困难吗？

教师：怎么做才能避开分类讨论呢？

学生5：不要把x-4除过去，保留ax-4a.

学生5的回答让其他的学生得到了启发.此时，有一位学生迫不及待地发表他的看法.

学生6：我想到不等式的左边可以视为过定点(4,0)的直线，右边视为函数y=2lnx-x2.整个不等式转化为直线y=ax-4a在函数y=2lnx-x2的图像的下方.

许多学生对学生6的理解有共鸣，给予掌声.

……

教师：我们要解后反思.解题遇到困难时，要寻找方法避开困难.使用分离参数法时，有时为了避免讨论，经常使用半分离参数的方法.在解题过程中，要有化归与转化的意识，这样就能在函数、方程、不等式三者之间进行灵活转化.把不等式转化成函数，利用直线与函数图像的位置关系分析问题，又是数形结合的数学思想方法的体现.

课堂教学中，突出学生主体是衡量一节课是否优秀的重要指标之一[2].学生能自主、合作探究解决的，教师不能一手包办；学生不能独立解决的，教师也不能越俎代庖，而是要给学生展示思维活动的空间，教师设置贴近学生真实背景和想法的问题串，为学生搭建脚手架，激活学生的思维，使学生体验到解决数学问题的快乐.在这种课堂活动中，学生能提升自己的学习能力，深化对数学知识本质的理解，并进一步学会用数学的思维方法去理解和解决数学问题.