从一道题谈解题教学中逻辑结构的构建

江苏省苏州阳山实验学校 (215151)

袁琴琴

解题信息论认为，数学解题的过程，就是数学问题信息的获取、存储、处理、输出，从而实现解题目标的活动过程.罗增儒教授则将数学解题过程总结为“三位一体”的工作：有用捕捉、有关提取、有效组合.为了真正意义上达到以上工作，首先要正确表征已有信息，而表征过程中较为适用的方式就是通过启发性提示语确定思维起点，进而与记忆储存中相关定理、公式、及其推理过程、基本模式(模型)等解题依据进行深度整合，形成解题时有效的逻辑结构.于是，捕捉信息与提取依据是形成逻辑结构的基础，是推进问题解决的源动力.在解题教学中若能展示逻辑结构的形成过程，则有可能对学生解题中的思维过程和心理过程进行恰当的分析，合理的调控，对培养学生的思维品质和心理表征能力有一定的帮助.本文试借一题谈谈对此的认识.

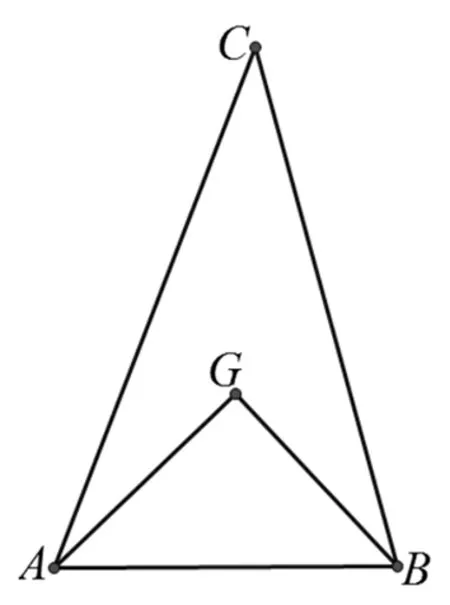
图1

看下面一道题：如图1，若点G为ΔABC的重心，且AG⊥BG，则sinC的最大值为 .

1.分析提示语，形成合理的思维方向

学生的知识结构和解题经验的个体差异，直接导致对已有信息产生强弱不一的心理刺激，即在已有认知“元”的调配下产生了最先“提示语”的自我认知，以自己熟悉(或熟练)的观点和方式作为思维活动的起点，并尝试调动已有认知动力，逐步揭开问题中各个未知信息.因此，我们应教学生捕捉到已有信息(包括条件与结论)中的“提示语”，通过对“提示语”的加工、解释、转换等方式，启发出正确的思维起点.

捕捉信息：问题中含有两个基本提示语——“重心”和“垂直”.

提示语分析：可以发现，这两个信息的最初表征与学生的元认知密切有关，不同的知识基础对信息理解的深度不一，进而产生不同的思维起点.

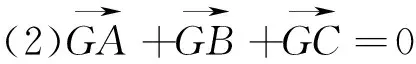
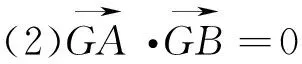
不难看出，对同一“提示语”的不同理解产生的思维起点不尽相同，不同的“提示语”下的思维起点却有可能相同，比如“重心”和“垂直”均可以从解析几何、向量等角度展开思维，同时也表明了不同的思维起点将会在过程中与其它信息产生交汇联系，形成一个和谐统一的逻辑结构.在教学中，让不同的学生暴露其表征已有信息的过程，并进一步暴露其产生的思维起点，让其他学生从中获取经验，长期训练，学生的表征能力将会得到很大提升.

2.模式构建，体现思维范式的引导性

我们经常遇到这样的现象：

课堂直接给出某一公式(定理)，然后给出大量训练题直接“运用”这一公式(定理)；

将某一问题改换叙述方式，或呈现新的情境，很多学生就束手无策.

上述现象是就题做题的短视教学行为，内在原因是教师没有将知识的生成、推导过程暴露给学生，必然不能揭示出过程中所蕴含的数学思想方法，学生在知识运用时出现思维卡壳断层的现象就不足为奇了.人教社章建跃教授在《中学数学课改的十个论题》中就着重指出：“要强调知识及其蕴含的思想方法教学的重要性.”因此，我们在新知识的教学中(特别是一些核心知识)，必须要不遗余力、不惜时间地体现出其过程性，并提升至思想观念层面去指导知识运用.

本题的思想方法源自哪里？我们回顾一下课本中推导“正弦定理”的过程：

传统推导正弦定理的基本方法有三个：

(暴露过程)

方向1：作高法——从几何量关系的角度去研究，蕴含“算两次”的基本思想；

方向2：坐标法——从解析几何的角度去处理，体现代数方法研究几何问题的基本准则；

方向3：数乘法——从向量运算的角度去思考，突出向量关系数量化的基本要领.

(小结提升)获得的思想方法：解决三角形(或几何图形)有关问题可以从几何关系、解析几何、向量运算三个基本方向进行思考.

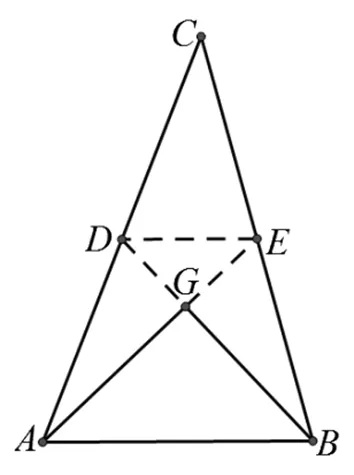
图2

通过暴露过程，小结提炼等活动的设计，为学生提供了具有思想性的先行组织者，在遇到类似问题时，就会自觉地将此作为一种思维的范式去进行：

本题是研究三角形中有关量的问题(问题识别)，可以将此与“正弦定理”的研究过程产生联系，从几何量的关系、解析几何、向量运算三个视角去展开思维(模式操作).

方向1：几何量的关系入手

分别延长AG、BG交BC、AC于E、D(如图2)，由勾股定理得

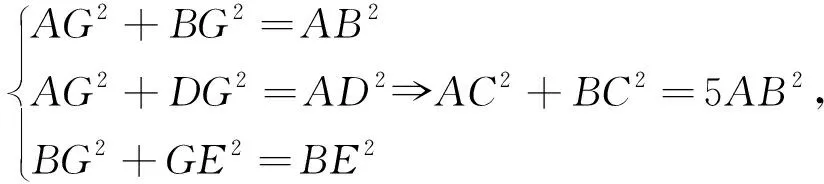
到体现.

方向2：解析几何的方法研究

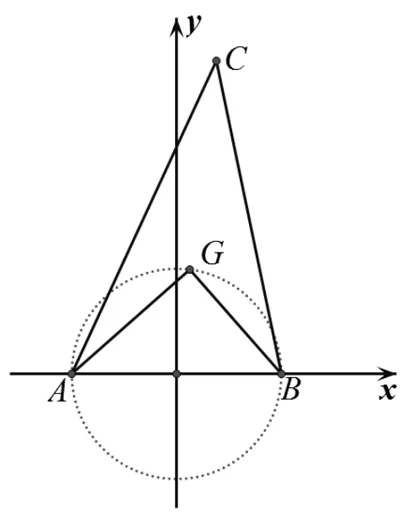
图3

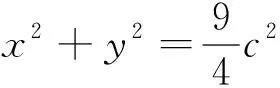
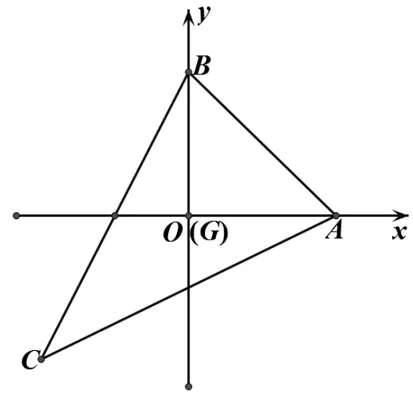
图4

建系2：注意到垂直的特殊性，以G为坐标原点，分别以AG、BG所在直线为x,y轴建立坐标系(如图4)，设A(a,0),B(0,b),C(-a,-b)，接下去可通过等面积、向量运算等进行处理.

方向3：向量运算着手

从上面的具体解答可得到验证，一旦有了核心知识蕴含的思想方法作为范式，学生必定能迅速进入思维通道.因此，在知识教学中一定要重视挖掘和揭示知识的思想性，并在知识运用过程中加以示范与训练，定会提升学生数学认知的理解程度.