对于数列中分式型递推关系的探究

江苏省常熟中学 (215500)

王 波

笔者在江苏省常熟中学工作，江苏省常熟中学起源是国立二中，是一所历史悠久，充满文化底蕴的学校，特别最近于2018年3月28日举办的80周年校庆，徐义刚和黄崇褀院士等校友以及各级领导的到来，充分肯定了江苏省常熟中学取得的成绩，为国家培养了大批的国家栋梁，长期以来保持在江苏省内高考成绩及竞赛第一梯队，学校有普通班，强化班，创新实验班三个类型，笔者一直以来带普通班和强化班，并负责强化班的竞赛工作，在平时的教学任务中，积累了一些教学的经验，先就数列分式型递推关系做一些探讨.

分式型递推关系在高三模拟卷和高考中常有涉及到，有时还包含着周期性一起考察，这类数列不仅考察等差数列和等比数列的基本知识和基本技能，还考察了特征方程和数列的周期性，对逻辑推理能力和分析解决问题的能力要求比较高.本文中，笔者通过平时的教学，把分式型数列的求解方法总结整理、归纳，并把一些思想和大家一起分享.

一、分子是常数，分母有an的递推关系，如型

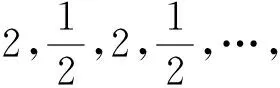
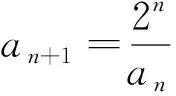
二、分子是常数，分母有an与常数的递推关系，如型

这种类型我们可以规定a1=1，这个类型我们不容易推导出它的通项公式，但是我们可以利用归纳猜想去做，其实所有的递推关系都可以用这种方法，后面的所有问题不再详细演示，很容易可以猜出通项an=1，第一步，当n=1时，a1=1，第二步，假设当n=k时ak=1，则n=k+1时，可以得到ak+1=1，得证.

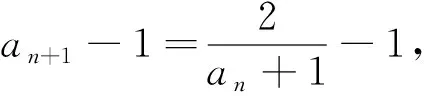
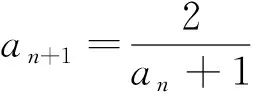
三、分子和分母都有an的递推关系，如型.

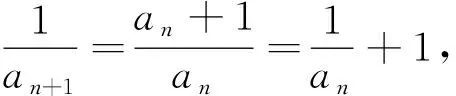
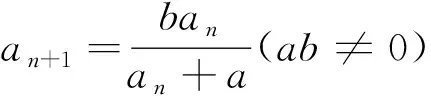
四、分子和分母都有an的递推关系，如型.

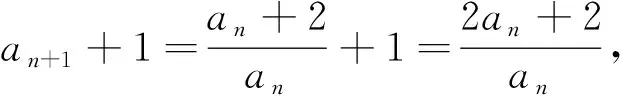
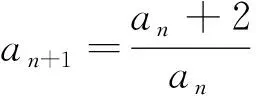
通过上面的各种类型的递推关系的求解，我们不难发现，对于分式型递推关系，一般的通法是对分式加减一个常数后，两边取倒数，构造一个等比数列去求解数列{an}的通项公式，下面我们对一般的分式型递推关系研究通项公式的一般证明步骤.

五、分子和分母都有an的递推关系，如型.

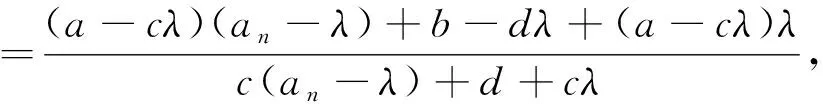
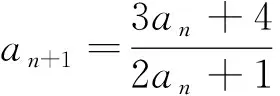
六、分式型递推数列求解的一般步骤及教学反思

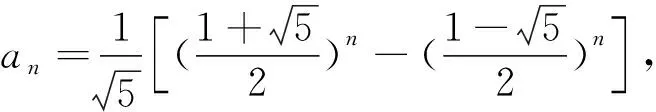
实际上我们还可以用另外的三项递推的方法研究这类递推关系，在竞赛班或者创新实验班上常常要讲这种方法，我们直接给出结论，不作证明，结论：如果x1,x2是递推关系an=pan-1+qan-2(a0,a1给定)的特征方程x2=px+q的两个根，则(1)当x1≠x2时，an=λ1x1+λ2x2；(2)x1=x2时，an=(λ3+λ4n)x1，这里λ1,λ2,λ3,λ4由题目给定的数据待定

我们研究了一次分式型递推关系的一些方法，对于二次分式型递推关系，或者高次分式型递推关系，以及非线性分式型递推关系，需要读者与专家一起努力，研究一些通法来求通项公式.