HPM视觉下的几道2018年高考数学试题赏析

浙江省金华市第六中学 (321000)

张剑平

近几年来HPM(History and Pedagogy of Mathematics)逐渐为中小学数学教师所熟知，2016年教育部考试中心公布了《关于2017年普通高考考试大纲修订内容的通知》，其中特别提出要关注数学文化.纵观近几年的高考试题，不难发现全国各地的高考试卷陆续出现了以数学文化为背景的试题.数学文化如何在高考命题中体现？笔者对近三年高考试题进行统计，高考命题以数学文化为背景的试题主要分布在以下两个方向：一是中国古代数学名著，考查频率最高的是《九章算术》，其次是《数书九章》《算法统宗》《张邱建算经》等.二是以中外数学家发现的相关定理、猜想为背景.本文笔者拟基于HPM视觉，分别从命题意图和命题背景来赏析2018年几道高考试题.

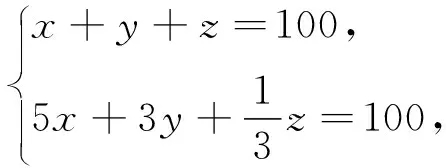
命题意图：作为填空题的第一题，应该是一道不难的题，但是也具有一定的考查价值，涉及到一些人文知识、阅读理解能力、以及心理素质.如果学生读不懂题目的意思，亦或心理素质较差害怕这类有文言文的题型，那么学生也不一定能做到.同时这道题目也在向考生传递一个信息，我国古代数学有着辉煌的历史，在公元前5世纪就会运用方程解决实际问题.

命题背景：《张邱建算经》，中国古代数学著作.现传本有92问，比较突出的成就有最大公约数与最小公倍数的计算，各种等差数列问题的解决、某些不定方程问题求解等.百鸡问题是《张丘建算经》中的一个著名数学问题，它给出了由三个未知量的两个方程组成的不定方程组的解.百鸡问题是：今有鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一.凡百钱买鸡百只，问鸡翁母雏各几何.自张邱建以後，中国数学家对百鸡问题的研究不断深入，百鸡问题也几乎成了不定方程的代名词，从宋代到清代围绕百鸡问题的数学研究取得了很好的成就.

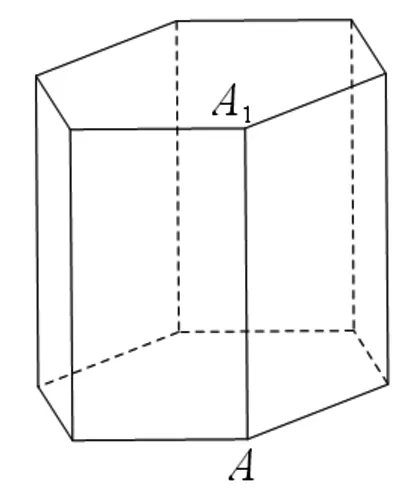
图1

例2 (2018上海15)

《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马.设AA1是正六棱柱的一条侧棱，如图.若阳马以该正六棱柱的顶点为顶点、以AA1为底面矩形的一边，则这样的阳马的个数是( ).

A.4B.8C.12D.16

命题意图：这道题以我国古代数学的经典名著——《九章算术》为切入点，题目中以书中的“阳马”概念为载体，考查了立体几何中的棱柱与棱锥，设计思路新颖.试题将数学文化有机地融入试题，改变以往立体几何命题背景单一的局面.

命题背景：《九章算术》始于公元前2世纪到公元3世纪，构筑了我国数学的基本框架，奠定了我国古代数学的发展道路，在整个中国以及世界产生了深远影响.《九章算术》蕴含着丰富的数学文化，让学生体会、欣赏数学的价值、感悟、理解数学思想，从而提高学生的数学素养，激发学生的创造能力.《九章算术·商功》：“斜解立方，得两壍堵.斜解壍堵，其一为阳马，一为鳖臑.阳马居二，鳖臑居一，不易之率也.第五章“商功”，主要讲各种形体的体积计算公式.涉及的几何体有长方体、棱柱、棱锥、棱台、圆柱、圆锥、圆台、楔形体等.问题的大都来源于营造城垣、开凿沟渠，修造仓窖等实际工程.

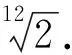
命题意图：音乐和数学密切相关，探讨音乐和数学的关系自古有之.题目也体现了多学科交叉渗透的命题趋势，懂一些乐理知识的考生理解题目更容易一些，当今中学生应该是全方位发展，让艺术教育逐步融入到文化课教育，培养综合型人才是大势所趋.

命题背景：十二平均律，亦称“十二等程律”,世界上通用的把一组音(八度)分成十二个半音音程的律制，各相邻两律之间的振动数之比完全相等.十二平均律是指将八度的音程(一倍频程)按频率等比例地分成十二等份，每一等份称为一个半音即小二度.一个大二度则是两等份.将一个八度分成12等份有着惊人的一些凑巧，钢琴师正是根据十二平均律来定音的.

例4 (2018全国Ⅰ理10)图2来自古希腊数学家希波克拉底所研究的几何图形．此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC，直角边AB，AC．△ABC的三边所围成的区域记为Ⅰ，黑色部分记为Ⅱ，其余部分记为Ⅲ．在整个图形中随机取一点，此点取自Ⅰ，Ⅱ，Ⅲ的概率分别记为p1，p2，p3，则( ).

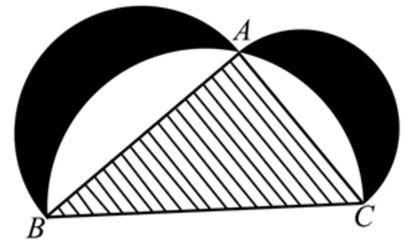
图2

A．p1=p2

B．p1=p3

C．p2=p3

D．p1=p2+p3

命题意图：以月牙定理为背景设计几何概型以及几何概率计算问题，情景陌生但是通俗易懂，通过本题的求解，使考生感受优秀数学文化的世界性，感悟数学之美.

命题背景：在初中教材八年级上册数学第43页的阅读材料中提到公元前约400年，古希腊的希波克拉底研究了他自己所画的图形，他得出了两个月牙形(图中阴影部分)的面积之和的一个结论：直角三角形两条直角边为直径向外做两个半圆，以斜边为直径向内做半圆，则三个半圆所围成的两个月牙型面积之和等于该直角三角形的面积，被称为月牙定理，这是古希腊数学家希波克拉底发现的一条平面几何里应用挺广的优美定理.

例5 (2018全国Ⅱ理8)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如30=7+23．在不超过30的素数中，随机选取两个不同的数，其和等于30的概率是( ).

命题意图：在高考试题中还是第一次出现我国当代数学家陈景润，命题者把我国当代数学史上的一个辉煌成就完美地融入到一个普通的概率问题中，同时也让考生对哥德巴赫猜想有了初步认识.一方面让考生感悟数学家不畏艰辛、不怕失败的精神；另一方面，让学生意识到猜想、创造对数学有多么重要，正是因为数学家们有开阔的视野和丰富的想象力，才把数学这门高深的学科不断推向前进，这是一种数学文化的教育，也是一种励志教育.

命题背景：哥德巴赫是德国的一位数学家，他在1742年提出了“任何一个大于2的偶数都是两个素数之和”的猜想，这个猜想如果被证明了，将会极大地推动数论研究的发展.200多年来，一代又一代数学家都在梦想证明它，它被列入20世纪最重要的数学问题之一.但是我国数学家陈景润在上个世纪70年代将它推进到“1+2”是一个了不起的进步，在国际数学界产生巨大的影响，被公认为是对哥德巴赫猜想研究的重大贡献.

2018年数学高考试题通过多种方式渗透数学文化，有的通过中国古代数学史展示我国数学文化对文明发展有着深厚和卓越的贡献，有的通过向考生揭示知识产生的背景和形成的过程来体现数学既是美妙的，也是曲折、坎坷的.在高考试题中渗透数学文化给我们的教学启示是：教师要关注数学文化，研究数学文化，更要引导学生关注数学文化，深刻地认识到中华民族优秀传统文化的博大精深和源远流长，数学史如何与中学数学教学融合在一起共同促进学生的发展值得我们数学教育工作者深思.