飞秒脉冲非对称互相关绝对测距∗

彭博 曲兴华 张福民 张天宇 张铁犁 刘晓旭 谢阳

1)(天津大学,精密测试技术及仪器国家重点实验室,天津 300072)2)(北京航天计量测试技术研究所,北京 100076)(2018年7月2日收到;2018年7月28日收到修改稿)

光学频率梳是一种重复频率与偏置频率锁定的新型光源,在频域上为频率间隔稳定的频率梳齿,在时域上为相对距离稳定的飞秒脉冲激光.光学频率梳在测距中的应用广泛,能够实现远距离高精度的测量.本实验使用飞秒激光脉冲作为光源,基于谐振腔扫描光学采样测距原理得到非对称的互相关干涉条纹,实现了远距离高精度的绝对测距.非对称互相关条纹可通过色散补偿与调节光学频率梳的重复频率得到,并通过得到的非对称的互相关干涉条纹对测距结果进行补偿.实验结果表明测距系统能够实现在50 m范围内误差为2µm的绝对测距,测量相对误差为1.9×10−7.

1 引 言

第17届国际计量大会将国际基本单位米与光在真空中的速度联系起来,光学频率梳作为一种新型的高稳定性的光源,成为时间与长度测量的重要工具.2000年,日本国家计量研究院的Minoshima和Matsumoto[1]首次将飞秒脉冲激光应用于绝对测距,并通过光学频率梳模间自拍频原理实现了大尺寸高精度的测量.此后,飞秒激光脉冲在测距中的应用越来越成熟与重要.光学频率梳测距方式[2,3]主要有合成波长法[1,4,5]、多波长干涉法[6,7]、色散干涉法[8,9]、飞行时间法[10,11]与光学采样法[12].本文采用光学采样法.光学采样法通过两个脉冲之间的扫描采样得到互相关干涉条纹实现测距,其分为位移台扫描法[13]、双光梳异步采样(asynchronous optical sampling,ASOPS)法[14]与谐振腔扫描光学采样(optical sampling by cavity tuning,OSCAT)法[8,15].其中位移台扫描法由于在测量过程中使用了机械结构而影响测量精度,且具有测量速度慢、不适用于大尺寸测量的缺点.ASOPS法测距系统复杂,且实验成本高.OSCAT法测距原理具有成本低、结构简单、易于实现等优点,因此本实验使用单光梳OSCAT法.OSCAT测距系统[16]通过非平衡迈克耳孙干涉仪得到测量光与参考光的互相关干涉信号,并通过互相关信号得到待测距离信息.

传统的OSCAT测距系统长延时光纤在参考臂[1,15−17],不利于实现任意距离的测量,且需要通过色散补偿光纤对经过延时光纤后的脉冲进行严格的色散补偿,来得到对称的互相关干涉条纹[18].当互相关条纹不严格对称时,在实际测量过程中由于脉冲形状的变化导致峰值偏移带来的测量误差无法评价,且无法通过该OSCAT测距系统实现单系统的绝对测距,需要外部仪器提供粗略测量.本实验将长延时光纤放在测量臂,使测距系统的非模糊范围随测量距离的增加而增加,易实现长距离的绝对测距.实验中利用非对称互相关条纹希尔伯特变换的两个波峰实现了测量过程中互相关条纹宽度变化的实时测量,通过宽度变化实现了测量过程中误差的补偿,并提出一种可行的单系统绝对测距方法.

2 原理及实验系统

2.1 实验系统

如图1所示,实验系统由两部分组成,分别为OSCAT测距系统与He-Ne激光干涉仪.OSCAT测距系统中激光脉冲光源重复频率为250 MHz,频率扫描范围为2.3 kHz.光源出射光通过光纤耦合器OC1分为测量光与参考光,测量光经过长延时光纤进入环形器,经过准直器、扩束镜后出射到目标靶镜,反射光通过环形器进入光纤耦合器OC3.其中长延时光纤为104 m单模光纤与12 m色散补偿光纤组成.参考光经过光纤耦合器OC2分为两部分,一部分进入光电探测器PD2产生自拍频,并通过计数器对光源重复频率进行测量,另一部分直接进入光纤耦合器OC3与测量光在光电探测器PD1发生拍频,并通过示波器进行数据采集.He-Ne激光干涉仪用于验证测距系统的测距结果的准确性.实验中光源重复频率的扫描需要的扫描电压通过函数发生器产生.

图1 测距系统Fig.1.Experimental setup of the measurement system.

2.2 测距原理

光电探测器输出信号强度可以表示为

其中Er(t)与Em(t)分别为参考光脉冲函数表达式与测量光脉冲函数表达式;E(t)为激光脉冲的包络函数;ωc为脉冲中心角频率;N为正整数;τ为测量光脉冲与参考光脉冲之间的时间延迟.其中(1)式的交流分量中的积分项为脉冲包络的自相关函数[19].

光学频率梳在真空中两个脉冲时域之间的距离Lpp表示为

其中c为真空中的光速,fr为光学频率梳的重复频率.由(2)式能够得到当测量距离与参考臂之间的距离满足一定关系使两个脉冲在空间中相互重叠时才能够发生拍频,OSCAT法正是通过扫描激光脉冲重复频率的方式对脉冲之间的距离进行调节实现拍频的方法.

实验过程中首先通过测距系统得到He-Ne干涉仪的零点对应的测距结果L0,然后移动被测点,记录移动过程中He-Ne干涉仪的测距结果与OSCAT测距系统的测距结果,被测点移动距离Lx可表示为

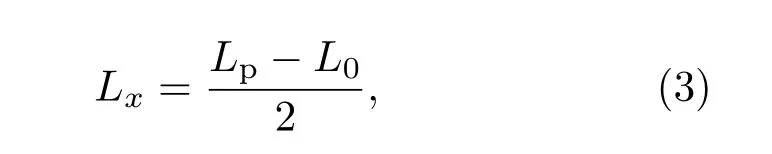
其中Lp为各个测量点得到的测距结果.

实验得到互相关干涉条纹的包络有两个波峰,两个波峰分别对应不同的扫描频率.互相关干涉条纹上任意两点之间的距离Ld可表示为

其中frp1与frp2分别为不同重复频率,且frp1

其中Ldelay为延时光纤的长度,Lmea为待测距离的长度,Lref为参考臂长度,nf为光纤折射率,n为空气折射率.由(4)式可得到测距系统的非模糊范围,系统测距非模糊范围由N及频率扫描范围决定.当frp1与frp2分别为两个波峰对应的重频时,则Ld为两个波峰之间的距离.由(4)和(5)式能够得到本测量系统的非模糊范围随着测距范围的增大而增大.当出射光在空间传播过程无折射率的影响时,即在真空条件下传播时,脉冲不会产生变形,不同测量点互相关干涉条纹是相同的,即不同测量点得到的互相关条纹两个峰值之间的距离Ld是不变的,这同时表明,通过标定得到互相关干涉条纹包络两个波峰之间的距离,就能够在测距过程中通过测量其对应的重复频率计算得到N,从而得到测距所需的全部未知量,实现单系统绝对测距.

在实际测量过程中发现在一个非模糊范围内两个峰值之间的距离变化量较大,这能够反映非对称性干涉条纹由于重复频率变化带来的峰值偏移误差、干涉条纹与重复频率采样同步性带来的误差以及测量系统稳定性带来的误差.通过测量非对称互相关条纹希尔伯特变换的两个波峰所对应的扫描频率的变化,对测距结果进行补偿能够有效地提高测距精度.

3 测量结果

经过测量参考激光脉冲宽度为730 fs,测量激光脉冲宽度为180 fs,因此测量激光脉冲与参考激光脉冲的互相关干涉条纹的宽度大约为910 fs,即互相关干涉条纹在时域上的宽度约为273µm.测量过程得到不同位置下互相关条纹如图2所示,测量环境条件为温度17.71◦C,压强995.80 Pa,湿度42.90%,基于Edlen公式[20]得到空气折射率为1.0002829.

由图2中互相关干涉条纹可明显得到,两个波峰之间的频率差随着测量距离的增加而减小,这与(4)式的分析结果相同,即随着N的增加,通过减小两个波峰之间的频率差来保持互相关条纹波峰时域上距离的不变.互相关条纹的强度随测量距离的增加而衰减.两波峰之间距离的测量值如图3所示.

图2 不同位置的互相关干涉条纹Fig.2.Cross-correlation patterns at different positions.

未补偿的测距误差有较明显的系统误差,经过相关性分析能够得到,峰值距离变化量与互相关条纹两个峰值之间的距离有较强的相关性,因此可通过互相关条纹两个波峰之间的距离的变化来修正测距系统误差.误差补偿表示为

其中δ1为补偿后的测距误差,δ0为未补偿的测距误差,∆d为峰值间距的变化量,p为比例系数.通过选择比例系数的值来达到较好的补偿效果,使补偿后的误差与峰值距离的变化量不相关,或相关性很弱.在5 m与35 m位置非模糊范围内比例系数p分别为0.32与0.60.

误差补偿结果如图4所示,图4(a)和图4(b)分别为在5 m与35 m位置非模糊范围内的测距误差.由补偿结果能够得到通过互相关条纹两个波峰之间距离的抖动对测距结果进行补偿,进而明显地减小测距误差,且随着测量距离的增加测距系统的非模糊范围在增加,与(4)和(5)式分析结果相同.

图3 非模糊范围内的峰值距离Fig.3.Distance between two peaks in non-ambiguity range.

图4 误差补偿Fig.4.Correction of deviation.

在0—50 m范围内不同位置进行了8次实验测量,测量结果如图5所示,实验结果表明本实验系统能够在50 m范围内实现误差为2µm的绝对测距.实验中测距的误差来源有重复频率的测量误差、光纤抖动的误差及空气折射率的测量误差,其中光纤抖动的测量误差较小且能够通过滤波有效地抑制,因此测距误差主要由重复频率测量误差及空气折射率的误差决定,频率测量的误差主要由频率测量速度与频率扫描速度之间的关系决定,可以通过提高频率测量速度或者降低频率扫描速度直接降低重复频率的测量误差.本系统频率测量误差∆f为23 Hz,带来的测距不确定度约为9.2×10−8×L(L为光程),空气折射率温度不确定度为15 mK,压强不确定度为5.3 Pa,湿度不确定度为0.13%,取扩展因子为2时合成不确定度为2.76×10−8×L.得到综合测距不确定度为进而可知在50 m范围内测距相对误差为1.9×10−7.

图5 远距离测量结果Fig.5.Experimental results of the long-distance measurement.

4 结 论

本实验通过扫描光学频率梳的重复频率得到非对称互相关干涉条纹,并通过非对称互相关条纹希尔伯特变换得到的两个波峰距离理论上的稳定性,提出待测距离中包含脉冲间隔数N的可行性测量方式,当测量系统稳定性较高时能够实现整数N的测量,从而得到一种基于非对称脉冲互相关单系统测距的方案.实验使用非对称互相关条纹进行测距,并通过互相关条纹两个波峰之间的距离变化对测距结果进行补偿,实验结果表明该实验系统能够实现50 m范围内误差为2µm的高精度测量,测量相对误差为1.9×10−7.