发现规律:让数学学习更简单
2018-11-30沈利明
沈利明

【摘要】《义务教育数学课程标准(2011年版)》指出:推理是数学的基本思维方式,也是人们在学习与生活中经常用到的思维方式。小学阶段是学生打好数学基础,初步了解数学学科特点并掌握相关计算能力和数学逻辑能力的一个阶段。
【关键词】应对 本位 借题而推
一、学生推理现状审视
1.“懂”与“不懂”的现象探问
在教学中,我们总喜欢问学生“懂不懂”“会不会”,学生异口同声回答“懂”“会”,但是一到做作业或者考试时总是会出现令人不太满意的结果。学生认为:上课认真听,看到了,听懂了,就学会了,学习任务就完成了。特别是低年级学生在做数学题时总是充满信心,认为把习题做完了,认真检查了,就什么都会。实际上,他们认为的“懂”只是在大脑里有短暂、浅表的印象,这不是“懂”,更不是“理解”。只是学生自己认为的“懂”。
2.“有序”与“无序”的钟摆现象
从幼儿园进入小学,学生心理从无所约束的天真感知,迈向接受为主、相对受约束的导向认知。数学不仅仅是爸爸妈妈和孩子嬉戏时的一种符号,而是实实在在的抽象。学生需要将自己对世界的感知与数学的符号、数学的语言联系起来,在这个过程中他们还缺少理解数学语言的能力,还缺少从生活世界中感知数学的能力,更缺少用数学的眼光和思想分析世界的能力。儿童的认知特点之一就是从简单想起,但是,儿童的思维又是跳跃性的,特别是刚入学的儿童,无所约束的直觉感知,可以说成“无序”。在这里“序”经常会被忽略。
二、兒童推理策略的实践探寻
1.借“境”而读,顺应认知的特点
小学生一开始对数学的认知和理解就是从归纳开始的,顺应学生认知特点不可或缺。教材给低年级学生提供丰富的形象画,架起了数学和生活之间的桥梁。但是这样的画面和学生看到的图画书不完全一样。对于学生来说,也许一张图就是一个故事,一片想象,但是数学上的图缺少了色彩的衬托,不利于学生天马行空地想象,这时数学教师的责任就是引导学生用数学的方法去“读”这些画面。比如,在认识数“0”时,课本出现以下图例。
学生学习时一般很难关注到兔子背后的数字世界。这时需要教师引导:“4只兔子一起采蘑菇,第一只小兔非常开心,因为它采到了3个蘑菇,那其他小兔呢?”学生因教师引导开始有序地读出图片后隐藏的数,2个、1个、1个也没有。这样的数学语言引导,让学生很快观察到了原本没有关注到的数字世界,从而自然而然地结合自己原有经验和图的意思,理解了“0”其中的一个意义——一个都没有。感知数字世界是学生学习数学的起点,让学生在开始阅读题目内容时就会注意图片文字背后隐藏的数字,感受到数字表达的意思,这就消除了他们数学学习的障碍。
2.借“图”而想,集聚归纳的过程
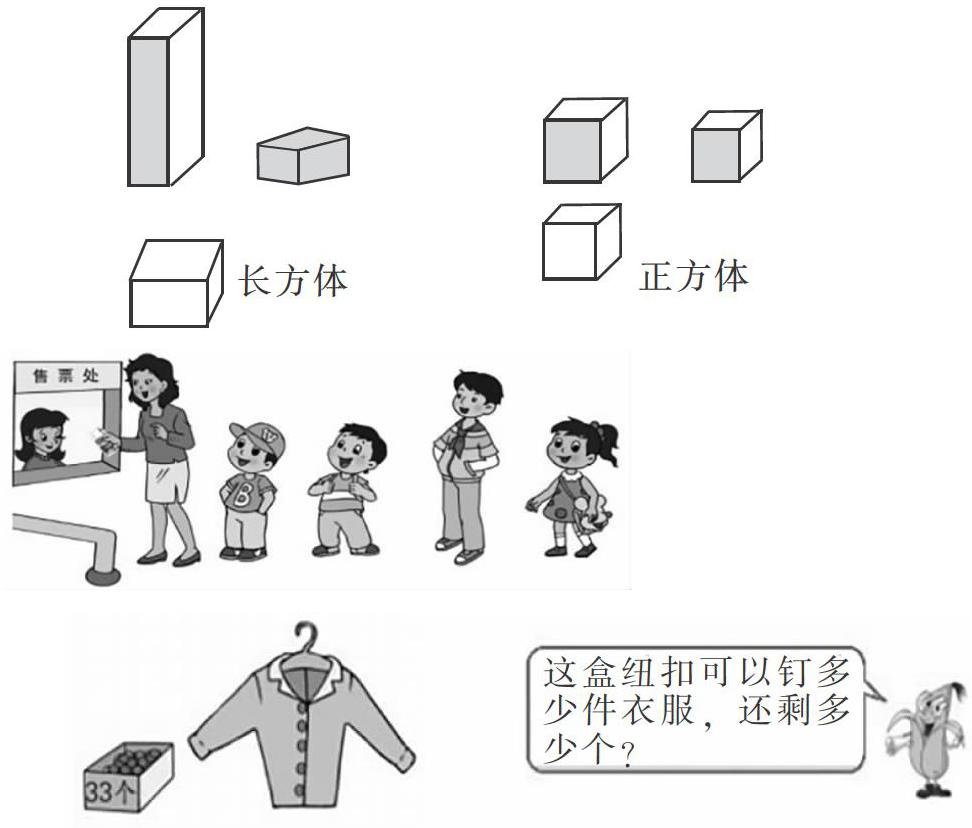
儿童以形象思维为主,小学数学教材中大量采用了猜想、归纳等推理方法。学生为获得事物的一般属性,必须在观察、实验、猜想等过程中投入更多的脑力活动。教师借助例题图,根据事物之间的内在联系,鼓励学生大胆展开联想,让学生在不完全归纳中聚集脑力能量,提升学生的推理能力。数学世界和现实世界最大的不同就是表达上的不同,数字和图形都是抽象的结果。从学生认数开始,抽象就展开了。如在一年级“认识图形”的时候,学生仅仅通过“长方体”“正方体”“圆柱”等文字和抽象化的数学图片很难对这些图形形成正确牢固的感知。
这时候,教师引导学生:“我看到黄色的长方体,想到了我家里的柜子”,学生马上可以模仿教师的话语展开想象,边看图,边说出想象的结果“想到家里的饼干盒是长方体”“我的玩具魔方是正方体”,等等,此时学生对课本中图片的关注就不仅仅停留在书本显示的内容,而是会与生活中的感知结合在一起,认识到课本上的图形就是对具有相同特点的生活中物体形状的总结。这种无法言喻的沟通就是抽象思想的基础,是渗透推理意识最关键的知识生长点。
3.借“题”而动,转换思维的方式
能力的提升不是一蹴而就的,它不同于知识与技能,需要学生通过自主感悟、体验规律以及思考等方式获得。而感悟只有在数学活动中自主体验才会更加深刻,促进能力进一步提升。因而教学活动必须为学生提供探索空间,并把学生推理能力的培养作为培养的首要任务,只有这样才能从“应对”真正走向学生“本位”。
如认识“几和第几”,这一内容主要是帮助学生区分“几”和“第几”的不同意义,是基数与序数的知识范畴。“几”表示一共有多少,而“第几”指的是事物的顺序,是其中的某一个。看似简单的描述,学生却很难理解。为了激活教学内容,在课堂实践中,教师组织了学生模拟类似的买票情境,学生们特别投入,学习积极性很高。在表达的过程中,学生都能用“几”和“第几”反映出位置的变化,更能体验到“几”和“第几”是不同概念。在活动过程中,结合学生自己对画面的阅读和理解用数学的语言表达出来。在课本的内容中变化是显现不出来的,通过现场模拟活动,将原本的文字或图片活化,学生自然就有了“动”的资源,数学本质的变化就通过“题动”而显现出来。
4.借“字”而思,类比事物的属性
儿童对于具体事物属性的感觉只是基础,并不能让他们完全了解此类事物的一般属性。现实世界中的数量关系往往有其自身的规律,用文字来叙述刻画的这种数量关系也会有分析、判断和推理的过程。这是一个经历观察、猜想、归纳、证明的过程,更是一个既有合情推理又有演绎推理的过程。学生对于文字理解上的缺失主要是生活经验相对较少,这就需要教师在教学中帮助学生构建文字与生活实际间的联系,让文字的意思显现出来为学生建构文字的理解模式。随着文字的理解,学生就能产生应有的情境想象,能第一时间帮助学生解决问题。如在苏教版一年级下册中有这样一道习题:
(1)玲玲养了30条,兵兵又送给她10条,玲玲现在有多少条?
(2)玲玲养了30条,送给兵兵10条,玲玲现在有多少条?
第1小题是“兵兵送给玲玲”结果是增加了,而第2小题是“玲玲送给兵兵”,结果是减少了,两题都有两人之间的“送给”行为,但结果截然相反。教师让学生读题后,用小棒代替“兵兵”摆一摆,学生在操作中感受“兵兵”送给别人与别人送给自己后的数量变化,这样,数量关系理解起来就比较容易了。学生从已知到未知的推理过程,深入探寻,类比出两道题有内在联系和有规律性的性质,最终归纳判断出结论,真正推动学生对数学本质的深入理解。
5.借“思”而想,概括出合理推断
严谨是数学学科的基本特点,无论是数学结论还是推断过程都需要逻辑性,推断必须建立在数学研究对象的准确分析及概括的基础上。由此,对于数学研究对象的分析及概括也决定着学生推理能力的高低。来自于生活中的数学问题其文字表达往往是生活化的,但是解决问题却需要数学化的理解,低年级学生将生活化的语言进行想象加工,才能正确理解问题的本质,才能运用相应的数学方法去解决问题。下面图例是一道与生活问题有关的题目,叙述的是一个钉纽扣的过程。如果学生简单读出题目的意思,而不能产生数学化的联想,那么解决它只能是一种对数学的简单感觉。
教师在教学中需要结合学生的初读,引导学生将问题数学化:“同学们想一想,这个过程具体是怎么操作的?”“就是在每件衣服上钉上5颗纽扣。”学生一般这样回答,教师追问:“那么这个过程和数学上的什么过程很相似呢?你会把问题换一种说法吗?”学生在这样的启迪下就会慢慢产生正确的联想:这不就是平均分吗?把33颗紐扣,平均5颗分给一件衣服。可以分多少件?还剩多少颗?学生这样的结合想象的转化,将问题直接指向了用除法解决的平均分问题。让学生在学习的过程中形成数学思考的习惯。这是一种基于审题思考之后的想象,将数学知识有针对性地运用到生活情境中。学生通过读题思考与想象的结合,把数学问题生活化,从而理解必要的过程和关系,也可以将生活问题数学化,找到相应的解决问题的模式和方法。学生在解决问题过程中,通过分析概括,进行合理判断。
在现实生活中很多活动能有效地发展人的推理能力。人们在日常生活中需要经常作出判断和推理,许多生活问题中也隐含着推理的要求,要让学生自主感受和感悟生活,并用数学眼光来观察思考。数学学习离不开推理思考,对于低年级学生来说,教师可以帮助他们通过习题思考,让他们一开始就接触数学的世界,从应对考试逐步走向本位,具有推理意识,同时,帮助他们理解问题的数学本质。
