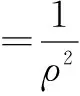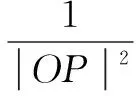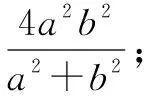分清椭圆离心角与旋转角

胡贵平

(甘肃省白银市第一中学 730900)

应用椭圆的参数方程解题时, 许多学生由于未能深入理解参数的几何意义, 没有准确把握椭圆参数方程中离心角与旋转角的区别与联系, 产生了误解，从而导致错误.

例已知P、Q是椭圆3x2+5y2=1上满足∠POQ=90°的两个动点，则OP2+OQ2=( ).

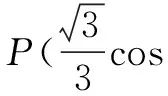
图1

错解分析回顾椭圆参数方程的推导过程，如图1，以原点为圆心,分别以a，b(a>b>0)为半径作两个圆,点B是大圆半径OA与小圆的交点，过点A作AN⊥Ox,垂足为N, 过点B作BM⊥AN,垂足为M, 求当半径OA绕点O旋转时点M的轨迹的参数方程.

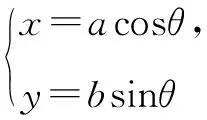
椭圆参数方程中的θ为离心角，∠AOx=θ，而旋转角∠MOx≠θ, 将旋转角∠MOx增加90°，离心角θ不一定增加90°， 那么离心角与旋转角有什么关系呢？

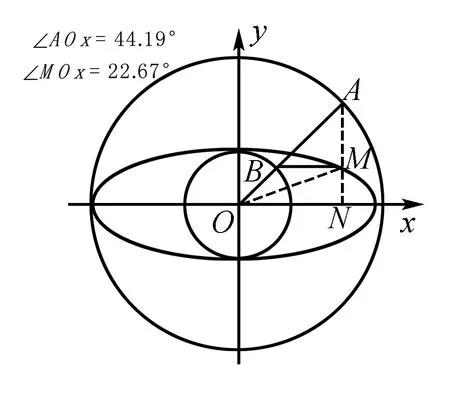
图2

通过几何画板动态显示，如图2，当拖动主动点A绕着点O转动时，离心角∠AOx和旋转角∠MOx的大小都在发生变化，可以观察出，在第一象限时，∠AOx>∠MOx；在第二象限时，∠AOx<∠MOx；在第三象限时，∠AOx>∠MOx；在第四象限时，∠AOx<∠MOx；当拖到坐标轴上时∠AOx=∠MOx，一共有四次相等的机会.

解法分析1.应用椭圆参数方程

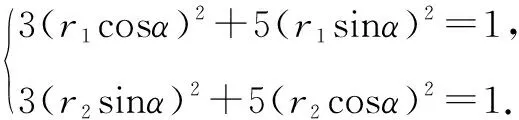
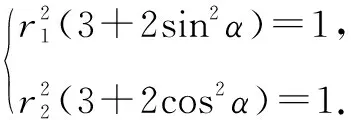
显然与夹角α的值有关，故选D．

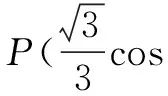
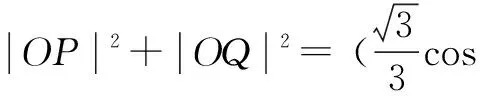
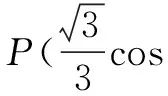
2.应用椭圆与直线位置

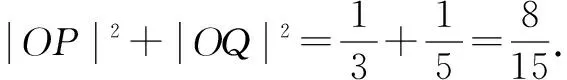
3.应用椭圆的极坐标方程

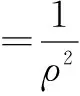
显然与极角θ值有关，故选D．

4.应用直线的参数方程

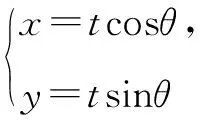
显然与倾斜角θ值有关，故选D．

分析解法同例题中各种方法，选一种比较简单的极坐标法．

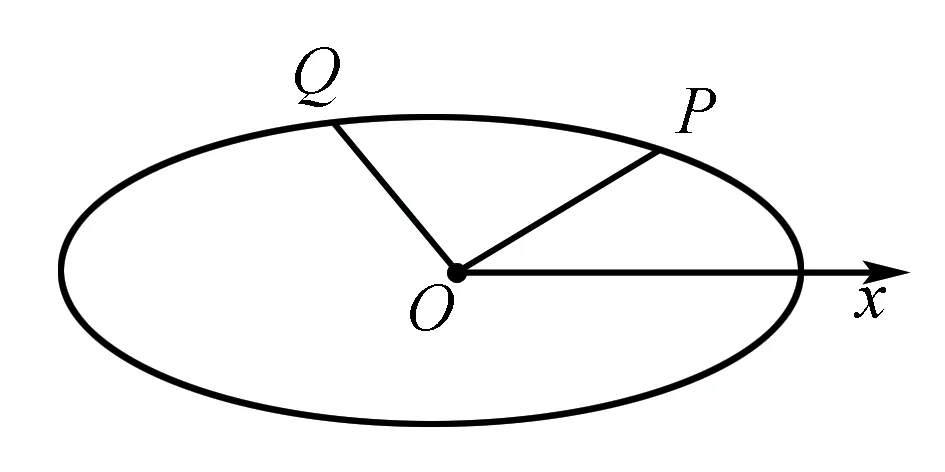
图3