浅谈整体法与隔离法是解题常用的思想方法

徐郅博

(江苏省响水中学 224600)

一、整体法、隔离法求解平衡问题

1.整体法的含义：所谓整体法就是对物理问题的整个系统或整个过程进行分析、研究的方法.

2.整体法的思维特点：整体法是从局部到全局的思维过程，是系统论中的整体原理在物理中的运用.

3.整体法的优点：通过整何不 地分析物理问是，可以弄清系统的整体受力情况和全过程的受力情况汇报，从整体上揭示事物的本质和变化规律，从而避开了中间环节的繁琐推算，能够灵巧地解决问题.

通常在分析外力对系统的作用时，用整体法；在分析系统内各物体(或一个物体的各部分)间相互作用时，用隔离法；有时解答一个问题需要多次选取研究对象，整体法和离法交替应用.

例1 有一直角支架AOB，AO水平放置，表面粗糙；OB竖直向下，表面光滑，AO上面套有小环P，OB上面套有小环Q；两环质量均为m，两环间由一根质量可忽略、不可伸长的细绳相连，并在某一位置上平衡，如图1所示.现将P环向左移动一小段距离，两环再次达到平衡状态，那么将移动后的平衡状态和原来的平衡状态相比较，AO杆对P环的支持力F、和细绳上的拉力FT的变化情况是( ).

A.F、不变、FT变大 B.F、不变、FT变小

C.FN变大；FT变大 D.FN变大，FT变小

解析本题先用整体法研究，再隔离分析.取P、Q两个环整体研究，在竖直方向上只有OA杆对其产生竖直向上的力(Q环不受杆向上的力)，故FN=2mg，FN大小不变.

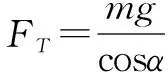
点评处理连接体问题时，一般优先考虑整体法，有时整体法和隔离法联合作用.

二、整体法、隔离法求解连接体问题

连接体问题是指在外力作用下几个物体连在一起运动的问题.在此类问题中，如果连在一起的物体具有相同的加速度，就可以将它们看成一个整体进行分析，即用“整体法”求解加速度；如果需要求解运动物体之间的相互作用力，就可以把各个物体分别作为研究对象，分析各自的受力情况和运动情况汇报，并分别列出方程求解，即用“隔离法”求解相互作用力.

1.整体法：昌将一组连接体作为一个整体看.牛顿第二定律F合=ma,F合是指研究对象所受的合外力，将连接体作为整体看待，简化了受力情况，因为连接体的相互作用力是内力而不是外力.在研究连接体的加速度与力的关系时，往往是将连接体视为整体.对牛顿第二定律F合=ma,F合是整体所受的合外力，ma是整体与外力对应的效果.注意分析整体受力时不要将内力分析在其中了.

2.隔离法：多是在求解连接体的相互作用力时采用.即将某个部分从连接体中分离出来，其他部分对它的作用力就成了外力.

说明处理连接体问题时，整体法与隔离法往往交叉使用，一般的思想是先用其中一种方法求加速度，再用另一种方法求物体间的作用力或系统所受合外力.一般有这样的规律：①求内力：先整体后隔离；②求外力：先隔离后整体.

例2 两个物体A和B，质量分别为m1和m2，互相接触放在光滑水平面上，如图3所示，对物体A施以水平的推力，则物体A对物体B的作用力多大？

解析对A、B整体分析，由牛顿第二定律有：

F=(m1+m2)a,①

再对B分析，同理有FN=m2a,②

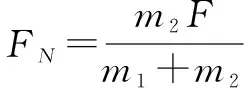
点评(1)上述解答过程先用整体法列出①式，即可求出a.再对B分析，列出②式代入a的值就可求出FN，这就是求内力就先整体后隔离.

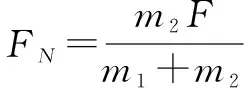
(3)求解此题也可以只用隔离法分别对A、B列方程：

对A：F-FN=m1a;对B:FN=m2a

事实上，对整体、对A、对B均可列一个牛顿第二定律的方程，其中两个方程求解即可.当然，最简单的还是列①、②两方程求解.

(4)上述例题可拓展如下(同学们可动笔推算一下)：

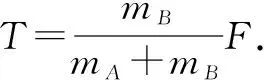
三、整体法隔离法的扩展作用

整体法作为一重要的研究方法在物理力学部分得到了广泛的应用，但大多局限于组成整体的各个个体加速度相同的情况汇报，其实，对于处理各个个体加速度不同的问题，整体法更能体现出它的方便与快捷.现结合以下两例讲述整体法在此时的应用.

例2 如图5所示，质量为M的框架放在水平地面上，它中间用两轻弹簧连着一质量为m的小球，当小球上下动，三角架对水平地面压力为零时，小球加速度的方向和大小为( ).

A.向上，Mg/mB.向上，g

C.向下，gD.向下，(M+m)g/m

析如果本题采用隔离法研究，此时需要讨论两弹簧的变形情况，会使问题变的复杂化，如果采用整体法，则可以使两弹簧的弹力成为内力，从而避免了讨论.

对整体做受力分析，整体在竖直方向上只受重力，则整体竖直向上受到的合力就是整体的重力，又整体受到的合力等于小球受到的合力与框架受的合力之和，所以有：(M+m)g=ma+Ma′，又框架的加速度a′=0，所以a=(M+m)g/m，方向与合力的方向即整体重力方面相同，竖直向下，所以答案为(D).

例3 如图6所示，倾角为θ、质量为M的木楔静置在粗糙水平地面上，有一个质量为m的物体以速度a沿斜面加速下滑，在此过程中木楔始终保持静止不动，木块与木楔间的滑动摩擦因素为μ，求地面对木楔间的摩擦力大小及其方向.

析如果用隔离法进行处理，需要分别研究木楔和木块，这样会使整个研究过程变的非常繁琐，我们可以这样思考，因为地面对木楔的摩擦力不仅作用在木楔上，而且作用在木楔和木块组成的整体上，所以我们可以采用整体法整体进行受力分析.因为整体在水平方向上只受地面提供的静摩擦力作用，所以整体水平方向上受到的合力即为该静摩擦力.在水平方向上有f=ma水平+Ma′.又木楔的加速度a′=0，所以静摩擦力的方向与木块加速度的水平分加速度方向相同，即沿水平向左，静摩擦力的大小f=ma水平=macosθ.

通过以上两例，相信对整体法的应用会有很深刻的认识.