指数式比较大小问题的方法探讨
2018-11-29李嘉宁
李嘉宁
(河北省衡水第一中学 053000)
一、单调性法
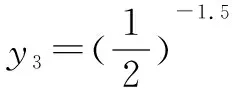
A.y3>y1>y2B.y2>y1>y3
C.y1>y2>y3D.y1>y3>y2
解析y1=21.8,y2=21.44,y3=21.5.∵y=2x在(-∞,+∞)上是增函数,∴y1>y3>y2.故选D.
温馨提示利用单调性比较大小,关键是化同底.
二、中间变量法
例2 比较1.40.1与0.90.3的大小
解析∵1.40.1>1.40=1,0.90.3<0.90=1,∴1.40.1>0.90.3.
温馨提示中间量法是指利用性质不易比较时,运用0、1等中间量进行比较,从而使问题获解.
三、分类讨论法
例3 比较52x2+1与5x2+2的大小.
思路点拔题中底数5>1,因此只要讨论幂指数2x2+1与x2+2的大小关系即可.
解析令2x2+1>x2+2,得x>1或x<-1;令2x2+1 ∵5>1,因此当x>1或x<-1时,52x2+1>5x2+2;当-1 温馨提示分类讨论是一种重要的数学方法,运用分类讨论法时,首先要确定分类的标准,涉及到指数问题时,通常在底数与1的大小关系确定后,再比较幂指数的大小. 例4 若0 温馨提示本题通过细心观察转化为同底型然后利用指数函数的单调性比较,其中转化是关键. 温馨提示本题关键也是转化,先将根式转化为分数指数幂,然后采用作差比较法比较指数的大小,再按底数进行分类讨论. 分析x1x2>0等价于x1>0且x2>0,或x1<0且x2<0,这样分别在(0,+∞),(-∞,0)上比较大小即可. (2)当x1<0且x2<0时, 例8 如图指数函数①y=ax,②y=bx,③y=cx,④y=dx的图象,则a,b,c,d与1的大小关系是( ). A.a B.b C.1 D.a 解析根据图象可先分为两类,③④的底数大于1,①②的底数小于1,再由③④中比较c,d的大小,由①②中比较a,b的大小.即当指数函数底数大于1时,图象上升,且底数越大时图象向上越靠近于y轴,当底数大于0小于1时,图象下降,底数越小,图象向右越靠近于x轴,故选B. 例9 函数f(x)=x2-bx+c满足f(1+x)=f(1-x),且f(0)=3,则f(bx)与f(cx)的大小关系是( ). A.f(bx)≤f(cx) B.f(bx)≥f(cx) C.f(bx)>f(cx) D.大小关系随x的不同区间而改变 解析∵f(1+x)=f(1-x),∴f(x)的对称轴为x=1,由此得b=2,又f(0)=3,∴c=3,∴f(x)=x2-2x+3在(-∞,1)内递减,在(1,+∞)内递增.若x≥0,则3x≥2x≥1,∴f(3x)≥f(2x).若x<0,则3x<2x<1,∴f(3x)>f(2x). 即总有f(3x)≥f(2x),故选A. 温馨提示本题是关于二次函数、指数函数单调性的复合问题,掌握二次函数的单调性以及指数函数图象的变化趋势是解决本题的关键.四、比较法
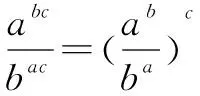
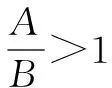
五、转化法
1.转化为同底型
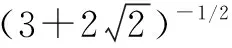
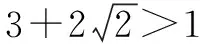
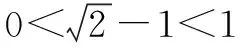
2.根式转化为分数指数幂
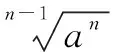
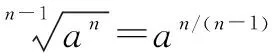
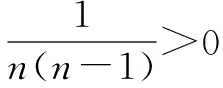
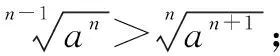
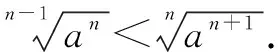

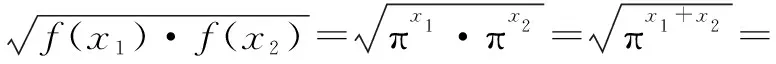
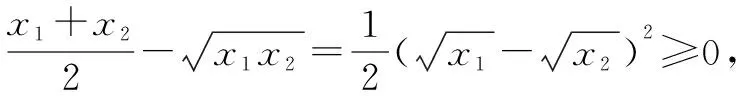
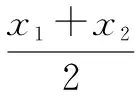
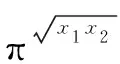
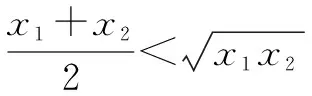
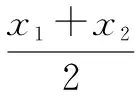
六、图象法