例谈排列问题的求解策略

张婉莹

(河北省任丘市第一中学 062550)

一、分类策略

例1 甲、乙、丙、丁四人互相传球，第一次甲传给乙、丙、丁三人中任一人，第二次由拿球者再传给其他三人中任一人，这样共传了4次，则第4次球仍回到甲的方法共有( ).

A．21种 B．42种 C．24种 D．27种

分析共传球4次，分四步完成，但应注意到第4次球仍回到甲，则第3次球不能传给甲．故第3次传球的方法与第2次球在谁的手中有关，又应分类处理．

解分四步完成：第一步由甲传给乙、丙、丁，有3种方法.第二步应分二类考虑：第一类传给甲，则第三步传给乙、丙、丁均可，第四步再传给甲；第二类不传给甲，则可传给甲以外的2人，第四步再传给甲.故共有3×(1×3×1+2×2×1)=21(种)方法，故选A.

例2 用0，1，2，3，4，5，6这七个数字,

(1)能组成多少个无重复数字的四位奇数？

(2)能组成多少个无重复数字且为5的倍数的五位数？

(3)能组成多少个无重复数字且比31560大的五位数？

分析(1)根据题意，分3步进行分析：①个位从1，3，5选择一个，②千位数字不可选0，从剩下的5个中选一个，③在剩下的5个数字中选出2个，安排在百位、十位数上，分别求出每一步的情况数目，由分步计数原理计算可得答案；

(2)分2种情况讨论：①个位数上的数字是0，②个位数上的数字是5，分别求出每一种情况的五位数个数，由加法原理计算可得答案；

(3)分析可得：符合要求的比31560大的五位数可分为四类分4种情况讨论，分别求出每一种情况的五位数个数，由加法原理计算可得答案．

解(1)根据题意，分3步进行分析：

(2)分2种情况讨论：

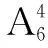
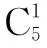
(3)符合要求的比31560大的五位数可分为四类：

第四类：形如3156□，共有2个.

二、倍分法策略

有些排列应用题，可以根据每个元素出现的机会占整个问题的比例，直接求得问题的解．

例3 有5个人并排站成一排，如果甲必须在乙的右边，则不同的排法有多少种？

例4 从6个运动员中选4个参加4×100米接力赛，若甲、乙两人都不能跑第一棒，则共有多少种不同的参赛方案？

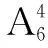
三、“捆绑”策略

例5 7人站成一排，求满足下列条件的不同站法：

(1)甲、乙两人相邻；

(2)甲、乙之间隔着2人.

分析两个都是元素相邻的排队问题，解决这类问题可先将相邻元素“捆绑”成整体并看作一个元素再与其它元素进行排列，然后再考虑相邻元素的内部排列.

评注首先把相邻元素当做一个整体参与运算，然后考虑相邻元素间的排列顺序.我们可遵循“先整体，后局部”的原则，即采用“捆绑”法.

四、定序问题缩倍法

例6 信号兵把红旗与白旗从上到下挂在旗杆上表示信号.现有3面红旗、2面白旗，把这5面旗都挂上去，可表示不同信号的种数是____(用数字作答).

评注在排列问题中限制某几个元素必须保持一定顺序称为定序问题.这类问题用缩小倍数的方法求解比较方便快捷.