基于数形结合思想的高中解题策略

芮欣妍

(江苏省扬州中学教育集团树人学校 225001)

华罗庚曾说：“数形结合百般好，隔裂分家万事休.”数与形从两个方面对数学知识进行描述和反映，数与形之间具有一一对应的关系.数形结合思想是一种重要的数学思想，尤其是在高中数学知识的学习和问题的解决过程中，科学地运用数形结合思想可以将数学的抽象语言、符号与几何直观的图形联系在一起，这样可以降低我们学习的难度，让我们更好地理解数学知识内涵，并能运用数学思想进行实际问题的解决.

一、数列与数形结合

数列是高中数学知识的重要组成部分，同时数列也可以归为函数的一种特例.在数列学习的过程中，常规的方法一般是用代数的方法进行分析和解决.如果在进行数列知识学习和问题分析的过程中，运用数形结合思想，将数列和几何图形建立对应的关系，往往可以起到事半功倍的效果.比如运用数形结合思想对下面的试题进行分析.

例1 已知等差数列an的前n项和为Sn，其中a1>0，3a8=5a13，那么，Sn最大的时候是( ).

A.S21B.S20C.S11D.S10

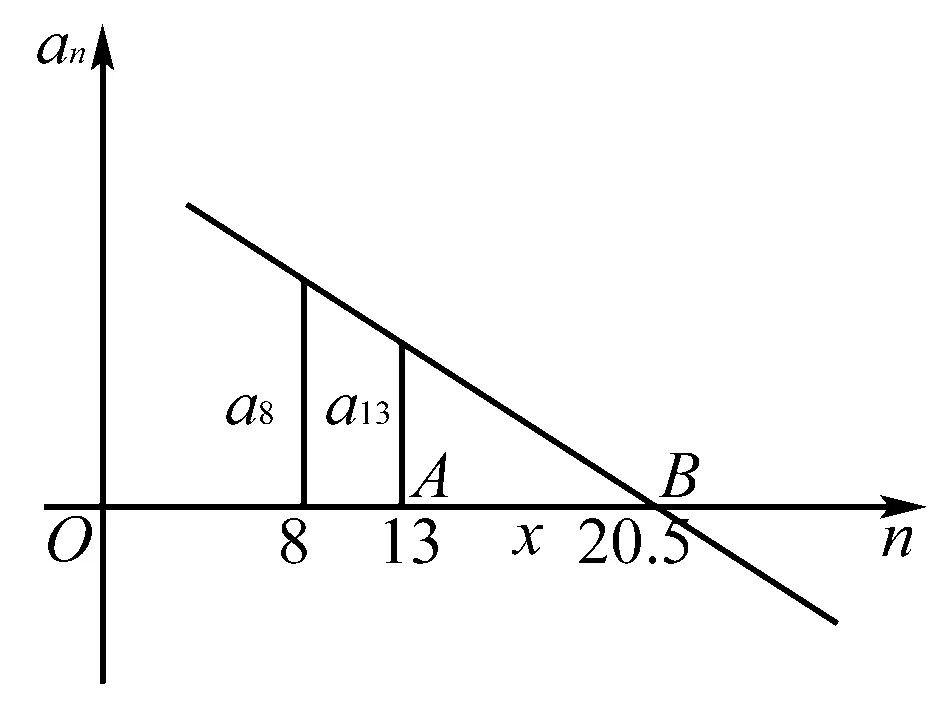
分析根据a1>0，3a8=5a13可以知道这个等差数列为递减数列，那么常规的方法需要求出等差数列第一个为负数的项，这样才能确定Sn的最大值，不仅计算麻烦，也不直观.而运用数学结合思想，可以通过3a8=5a13，作出等差数列的直线图形(如右图)，然后根据相似三角形的知识可以求得直线与x轴的交点，从而直观地得出所要求的答案.

在数列的学习中，等差数列的项一般分布在一条直线上，等比数列的项分布在指数函数图象上，我们在学习的过程中，通过数列和函数图象之间的对应关系进行实际问题的分析，不仅能提高学习效率，同时也能增强思维能力，提高运用数学思想的意识.

二、集合与数形结合

在高中数学集合知识中运用数形结合思想，可以将集合抽象的代数形式转化为直观的集合图形，从而提高集合知识的直观性.运用数形结合思想进行集合问题的分析，可以将集合中的数量关系转化为几何图形，并且通过方程将二者对应起来，这样对于一些比较复杂的集合问题的解决具有良好的效果.

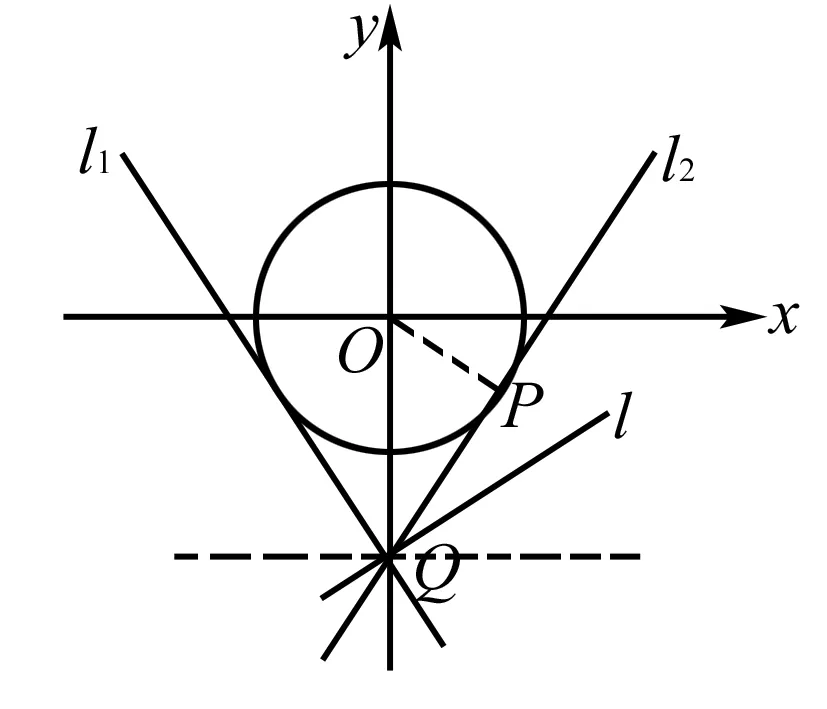
例2 已知集合A=(x,y)x2+y2=1，B=(x,y)kx-y-2≤0，且x,y∈R，那么A⊆B的时候，实数k的取值范围是多少？

分析根据题意可知，集合A为一个圆形，并且位置固定，而集合B是一条过点(0，-2)的直线，当A⊆B的时候，就需要考虑集合B直线的范围，如果运用数形结合思想作出集合的图象，问题就一目了然了.

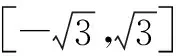
三、三角函数与数形结合

三角函数是高中学习的重点，同时也是高考的难点，通常情况下，通过数形结合思想的运用可以有效地解决三角函数的值域、证明等问题.将复杂的三角函数运用代数的方法构造出新的函数，然后转化为几何图形，可以有效地提高问题的解决效率，达到出奇制胜的目的.

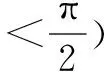
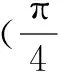
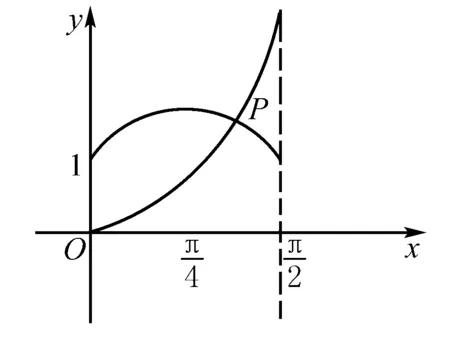
分析本题如果对三角函数直接进行计算，不仅复杂，运算量大，同时也不一定能够计算出来，因此可以构造两个函数，令f(x)=sinx+cosx，g(x)=tanx，然后再作出这两个函数的图象，通过图象上的交点可以轻松地解答问题.

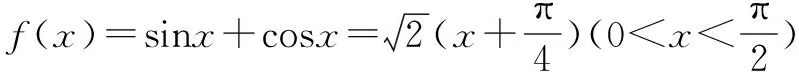
总之，在高中数学的学习中进行数学思想的运用，可以有效地掌握数学规律，深入到数学知识的内部，从而提高学习效率.数形结合思想是我们高中生必须要掌握的一种数学思想方法，不仅是在数学问题的探究中具有重要的作用，同样对于我们以后的数学学习和发展也具有重要的意义.因此，我们要在数学实际问题的分析和探究中，有效地运用数形结合思想，提高学习效率.