多角度对解析几何进行坐标化

魏冉军

(江苏省丰县中学 221700)

解析几何是用代数方法研究几何图形的一门科学…….这样，如何把解析几何进行代数化就显得尤为重要.在涉及点的坐标时，是引入直角坐标x,y，或是引入三角函数形式的坐标、极坐标；在涉及曲线方程时，是利用直角坐标方程，还是使用参数方程、极坐标方程，或者是其它形式的坐标方程.现阶段无论是教师还是学生，都比较青睐直角坐标x,y，而对其它形式没能引起足够重视.下面笔者以2018年江苏高考解析几何题为例，多角度对解析几何进行代数化.

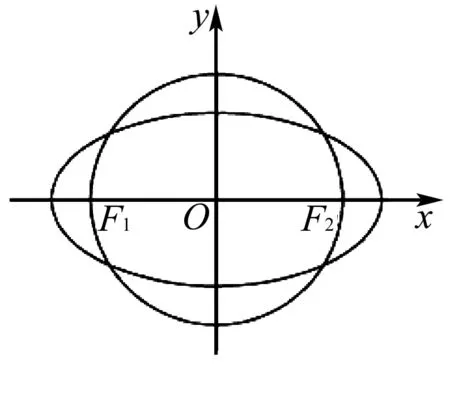
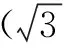
(1)求椭圆C及圆O的方程；

(2)设直线l与圆O相切于第一象限内的点P，

①若直线l与椭圆C有且只有一个公共点，求点P的坐标；

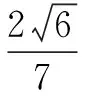
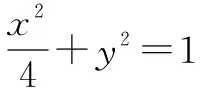
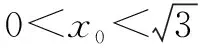
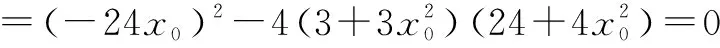
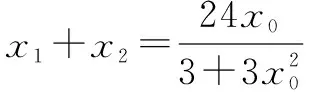
角度2 采用直角坐标的形式，直接设出直线方程(根据条件有时可以设直线的参数方程、直线的极坐标方程等形式)，使用直线方程中的基本量来表示其它关系，具体为：①设直线l的方程为y=kx+m，其中k<0，m>0.

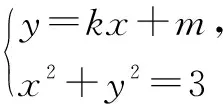
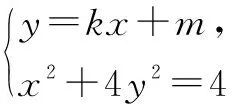
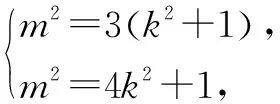
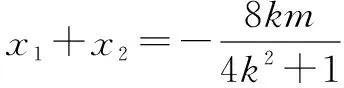
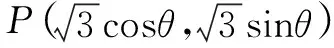
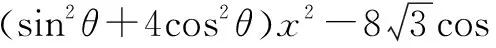
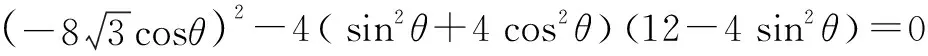
②设Ax1,y1,Bx2,y2，由(﹡)得x1+x2=

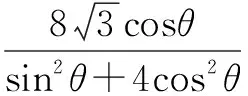
因此，解析几何代数化(坐标化)的一般方式有两种：第一，直接设点坐标(何种形式要思考)，然后坐标化相关问题；第二，设直线方程(设何种形式要思考)，通过联立方程表示坐标，然后再进行坐标化.一般的，若直线与椭圆相交，且需要两点坐标，则更多地选择设直线方程；若直线与椭圆相交，而只需要其中一点，则更多地选择设该点坐标.另外，解析几何题也不妨从几何性质这个角度出发，性质研究得越充分，计算就会越简单，读者不妨多试一下，但是有的时候这种思路难以想到，不容易形成数学思想方法，很难复制到其它数学问题中.