数学通报中若干三角问题的推广、改进或优化
2018-11-28黄兆麟
黄兆麟
(天津水运高级技工学校 300456)
《数学通报》的问题解答栏中每期的五个题各具特色,就象数学世界海洋里的五颗珍珠绚丽多彩,令人赏心悦目且能启迪人们的智慧,在充分享受原解美妙方法的同时也提高自己的鉴赏能力.通过研究学习,笔者发现该栏目或其它栏目有一些三角题或定理均有推广、改进或优化的空间,现介绍如下,与解题爱好者共赏.
问题2223在△ABC中,求证
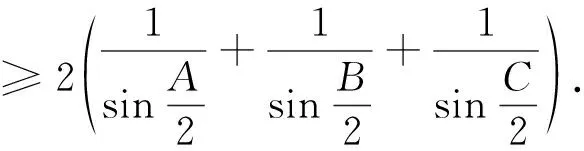
这是一个结构简洁优美对称的三角不等式,原解答利用换元法求解但不易推广,本文给出其指数推广的简捷证明,供参考.
推广命题1在△ABC中,已知p>0,则有
证明由待证不等式的全对称性,
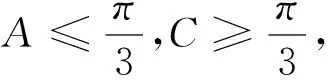
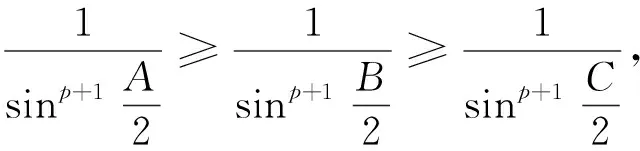
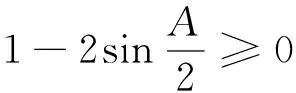
又设待证不等式左右之差为M,则
显然2223题是以上推广命题1当p=1时的特例.
问题2243在三角形ABC中,a,b,c,ma,mb,mc,ha,hb,hc,R,r分别表示三边长,三条中线长,三条高,外接圆、内切圆半径,求证 :
这是一个较弱的三角不等式,本文给出其加强指数推广的简捷证明,且证明并不涉及到两圆半径,供参考.
推广命题2设a,b,c,ma,mb,mc,la,lb,lc,ha,hb,hc,s分别表示△ABC的三边长,三条中线长,三条角平分线长,三条高线长和半周长,若指数p>0,则有
证明注意到有中线长公式、角平分线长公式及高线长公式,立得
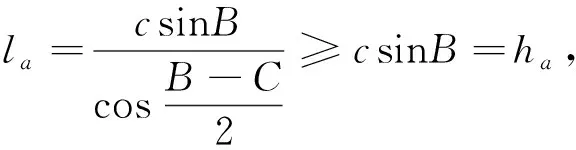
那么就有ma≥la≥ha,
从而可得

故知推广命题2中的不等式链成立.
问题2296在锐角△ABC中, 求证:
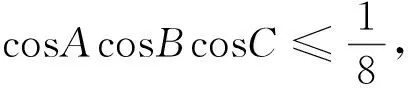
证明直接由三元均值不等式及熟知成立的不等式
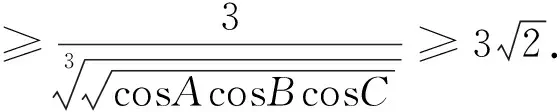
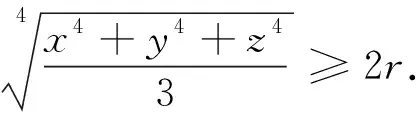
原证曹嘉兴老师利用四点共圆、柯西不等式及两个熟知的三角几何不等式给出了证明,指数推广不易,该题若借助于艾尔托斯—莫迪尔不等式即可给出该题指数推广的简证.
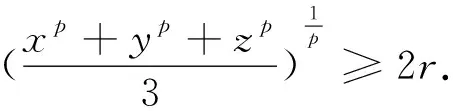
证明由幂平均不等式不等式(p>1)可得
又设P点到△ABC三边BC,CA,AB的距离分别为u,v,w
那么由(P.Erdos-L.J.Mordell)艾尔托斯-莫迪尔不等式
x+y+z≥2(u+v+w),
我们立得
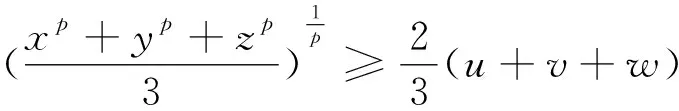
(*)
当取P点为△ABC的内心时,
就有u=v=w=r,
故推广命题3成立.
显然2300题是以上推广命题3当p=4时的特例.
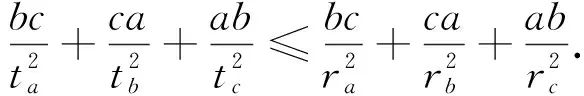
推广命题4在△ABC中,若a,b,c;ra,rb,rc;ha,hb,hc;ta,tb,tc;Δ,p分别表示三条边,旁切圆半径,高线长,内角平分线长,面积和半周长,且指数m>0,n≥1,则
(1)
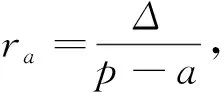
当n≥1时,由幂平均不等式有
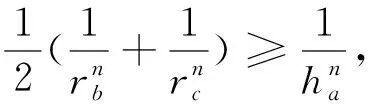
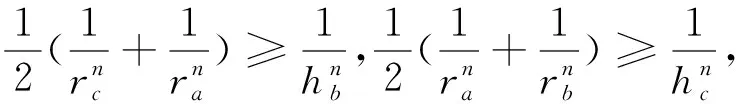
以上三个等式相加即得
(2)
下面首先证明链(1)中第一个不等式.
由于链(1)中第一个不等式的完全对称性,
不妨设a≥b≥c,则有3a≥2p且3c≤2p,
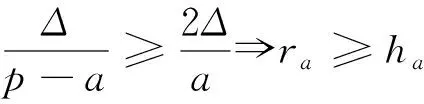
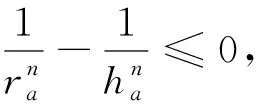
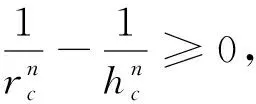
设链(1)中第一个不等式的左右之差为M,则有
即链(1)中第一个不等式成立.
以上证明最后一步用到了不等式(2)成立的结论.
最后证明链(1)中第二个不等式.
由ta≥ha,tb≥hb,tc≥hc,知有
三式相加立得
即链(1)中第二个不等式成立.
至此推广命题4的不等式链(1)获证.
问题2373在△ABC中,三内角A,B,C所对三边长分别为a,b,c,面积为Δ,求证:
(a+b-c)2+(b+c-a)2+(c+a-b)2
原证曹嘉兴老师利用换元法给出了一种代数形式的证明,该题若借助于费恩斯列尔-哈德维格尔不等式,便可直接获证.
证明只要将待证不等式左边展开再整理立得
a2+b2+c2+(a-b)2+(b-c)2+(c-a)2,
再移项合并立得费-哈不等式
a2+b2+c2
即待证不等式与费-哈不等式等价,故知待证不等式成立.
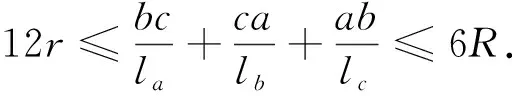
胡文生老师在证明不等式链右边的上界不等式时稍显复杂,其实胡老师在证明下界不等式时,都已经得到了证明上界需要的等式
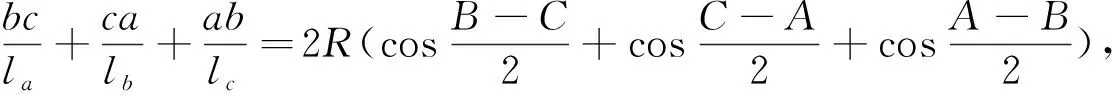
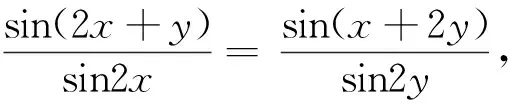
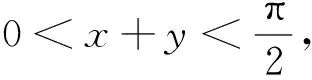
原解答利用Steiner-Lehmus定理:“在三角形中,若有两个内角的角平分线长相等,则该三角形为等腰三角形。”给出的证明,本文则给出一种反证法的证明,实际上也是给出了Steiner-Lehmus定理一种反证法的证明.
证明(反证法)首先将条件等式去分母,可得
sinx[sin(x+2y)cosx]=siny[sin(2x+y)cosy]
⟹sinx[sin2(x+y)+sin2y]=siny[sin2(x+y)+sin2x]
⟹sin2(x+y)·(sinx-siny)=2sinxsiny·(cosx-cosy). (*)
注意到题设条件,立知sin2(x+y)>0,2sinxsiny>0
①假设x>y,那么此时(*)式左边>0,同时(*)式左边<0,矛盾!故假设不真!
②假设x
综上①和②,立得x=y

设(p-a)(p-b)=x,(p-b)(p-c)=y,(p-c)(p-a)=z,
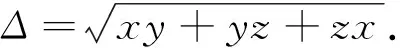
以上定理是曹嘉兴老师给出的(见文[2]),本文则给出一个较为简洁的证明,供读者参考.
证明由半角正切公式、余弦定理及海伦公式,可得
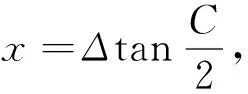
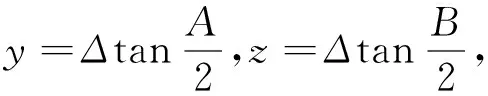
那么就有
以上证明过程用到了不等式
