数学问题解答
2018-11-28
(解答由问题提供人给出)
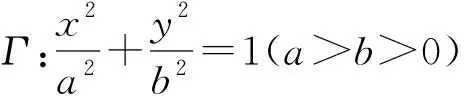

(山东省泰安市宁阳第一中学 刘才华 271400)
证明设A(x1,y1),B(x2,y2),C(x3,y3),由O为椭圆Γ的中心,得
x1+x2+x3=0,y1+y2+y3=0.
由C(-x1-x2,-y1-y2)在椭圆Γ上得
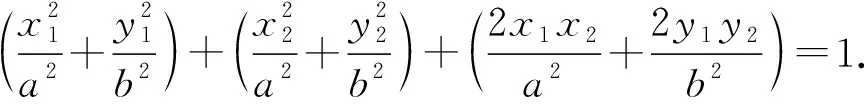
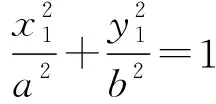
即
(1)
由过点B的椭圆Γ的切线方程为
(1)式表明切线DF过点(-2x1,-2y1).
同理由B(-x1-x3,-y1-y3)在椭圆Γ上得
(2)
由过点C的椭圆Γ的切线方程为
(2)式表明切线DE过点(-2x1,-2y1).
从而D(-2x1,-2y1).同理得
E(-2x2,-2y2),F(-2x3,-2y3).
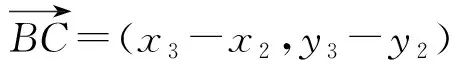
于是线段BC为△DEF边FE对应的中线,从而B为线段DF的中点,C为线段DE的中点.同理A为线段EF的中点,故S△DEF=4S△ABC.
2442已知a,b,c为正实数,且ab+bc+ca=1,试证明:
(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000)
证明由条件等式ab+bc+ca=1,

当a=b,2ab=1,而ab+bc+ca=1,
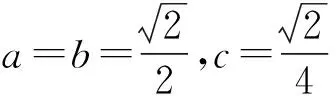
2443已知:如图1,PA、PB、PC、PD为⊙O的顺时针排列四条弦,且∠APB=∠DPC.若AD为⊙O的直径.求证:
2PB·PC≤(PA+PD)2.
(北京市芳草地国际学校富力分校 郭文征 郭璋 100121)
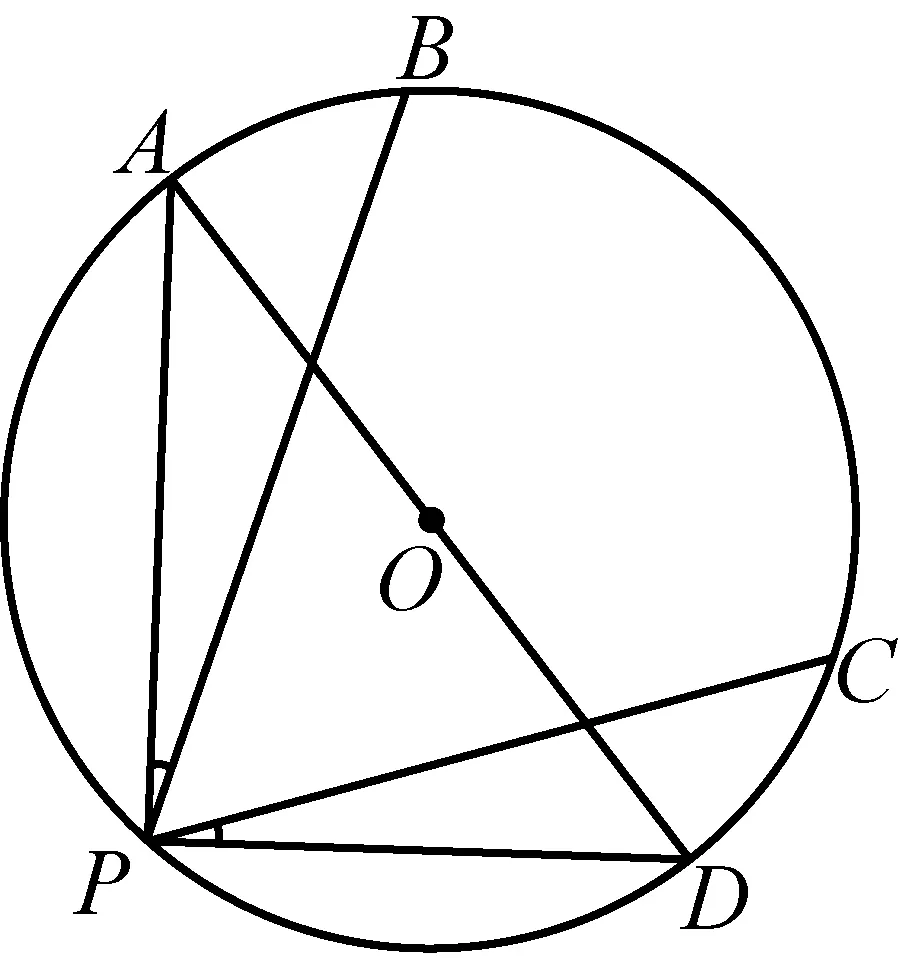
图1
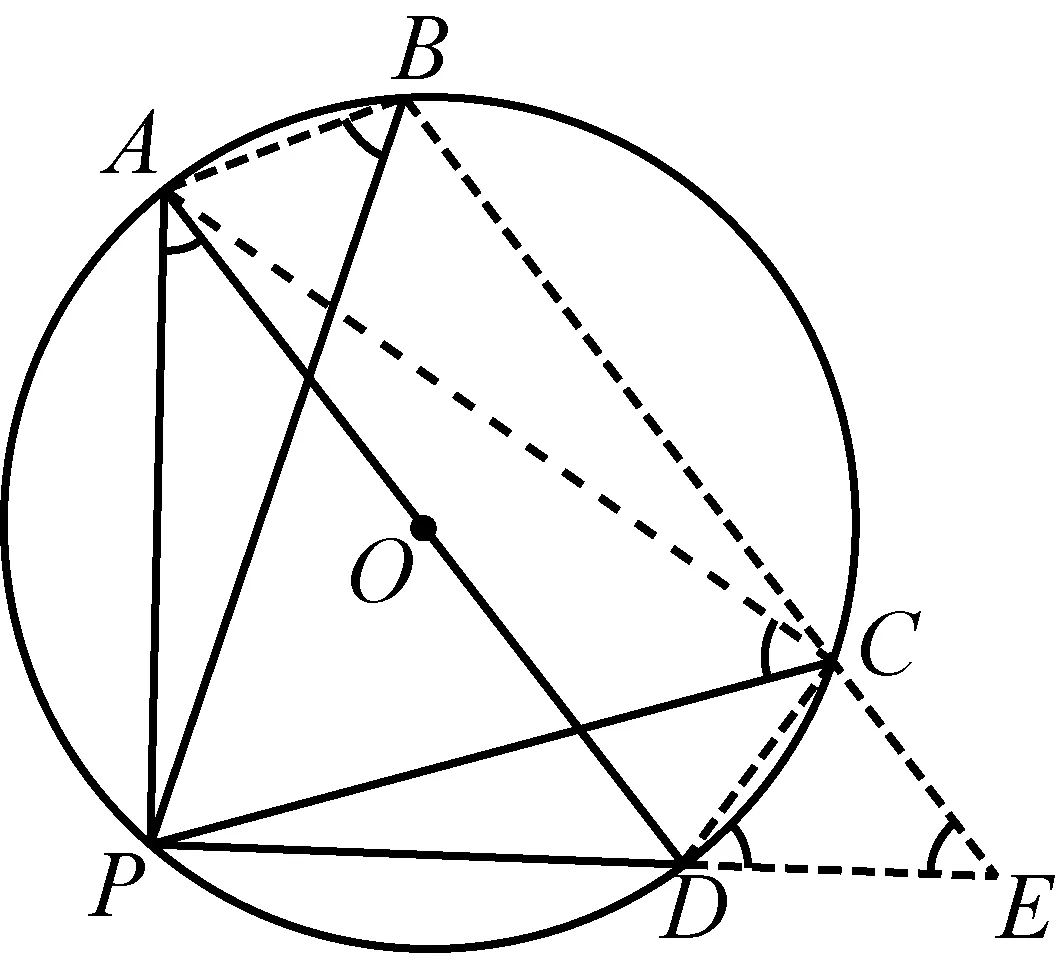
图2
证明如图2,连接AB、CD、AC,连接BC并延长与PD的延长线相交于点E.
因为P、C、B、A四点共圆,
所以∠PCE=∠PAB.
又∠APB=∠DPC,即∠APB=∠CPE.
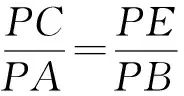
⟹PB·PC=PA·PE=PA·(PD+DE)
=PA·PD+PA·DE.
(Ⅰ)
因为P、D、C、A四点共圆,
所以∠EDC=∠CAP.
因为P、C、B、A四点共圆,
所以∠PBA=∠PCA.
由△APB∽△CPE,
可知∠PEC=∠PBA,
所以∠PEC=∠PCA.
即∠DEC=∠ACP.
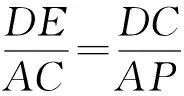
⟹DE·PA=AC·DC.
(Ⅱ)
由(Ⅰ)、(Ⅱ)两式得
PB·PC=PA·PD+AC·DC
⟹2PB·PC=2PA·PD+2AC·DC
⟹2PB·PC≤2PA·PD+AC2+DC2.
(Ⅲ)
因为AD为⊙O的直径,
所以∠APD=90°,∠ACD=90°.
所以PA2+PD2=AD2=AC2+CD2.
(Ⅳ)
由(Ⅲ)、(Ⅳ)两式得
2PB·PC≤2PA·PD+PA2+PD2.
故 2PB·PC≤(PA+PD)2.
因为∠APB=∠DPC,
所以PB、PC为∠APD的内等角线.
当且仅当PB、PC重合为∠APD平分线PB时,不等式中等号成立.
2444已知△ABC三边长,外接圆半径及内切圆半径分别为a,b,c,R,r,则有
(天津水运高级技工学校 黄兆麟 300456)
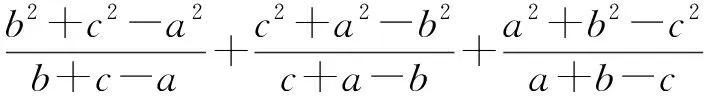
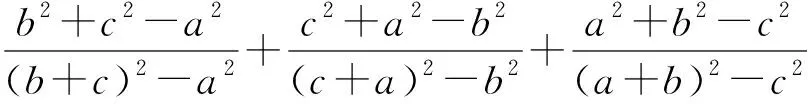
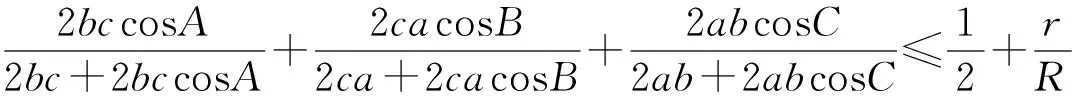
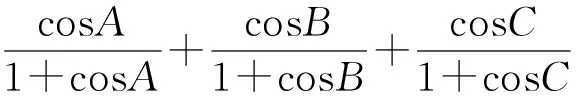
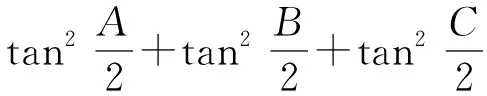
而以上最后一个不等式是熟知的Garfunkel—Bankoff不等式,显然成立,故原不等式成立.
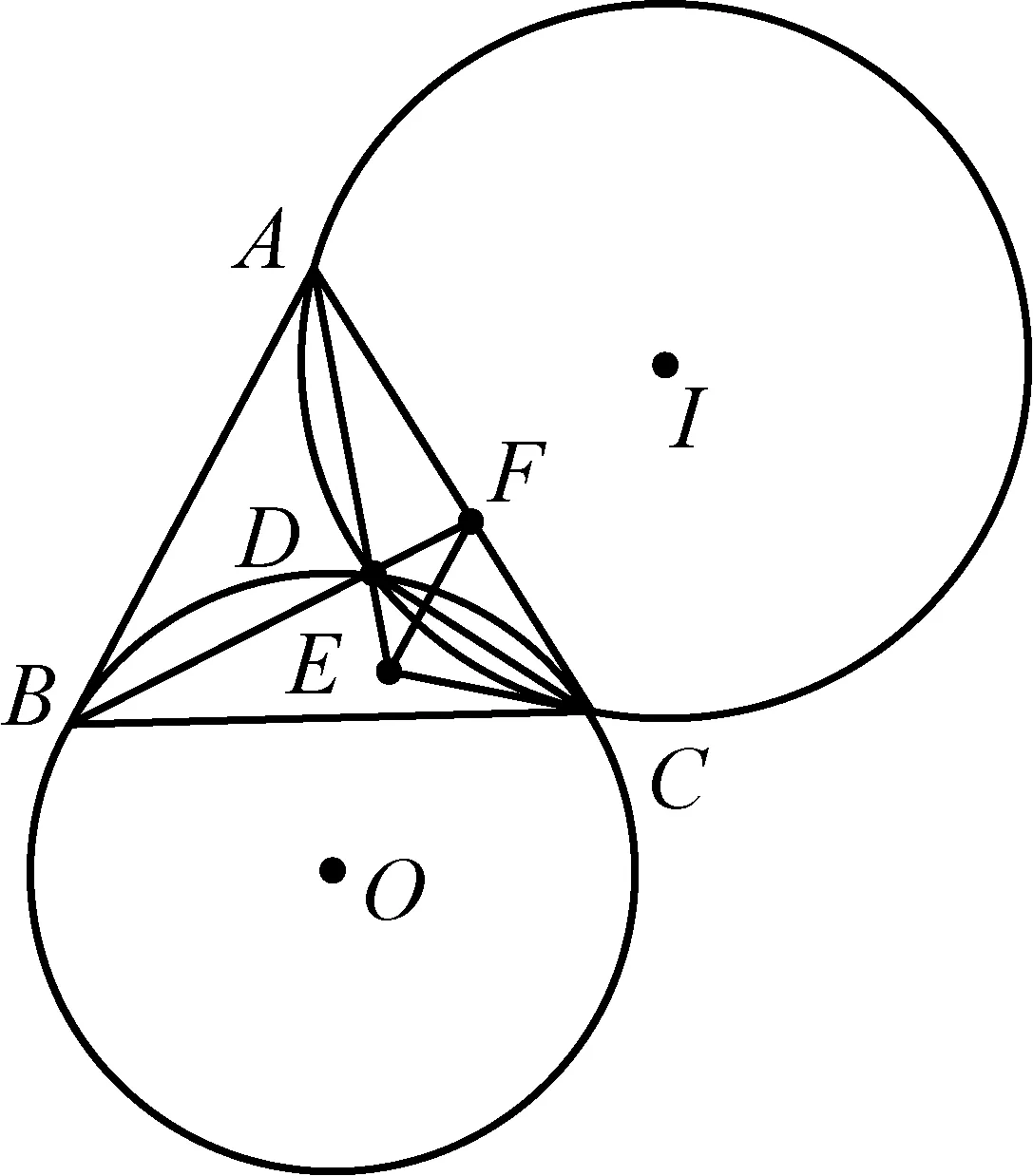
2445如图,△ABC为等边三角形,⊙I过A、C两点,⊙O与AB、AC相切点B、C,两圆交D点,延长BD交AC于F,过⊙I点C作切线交AD延长线于E,
求证:AB∥EF.
(江西师范高等专科学校 王建荣 335000)
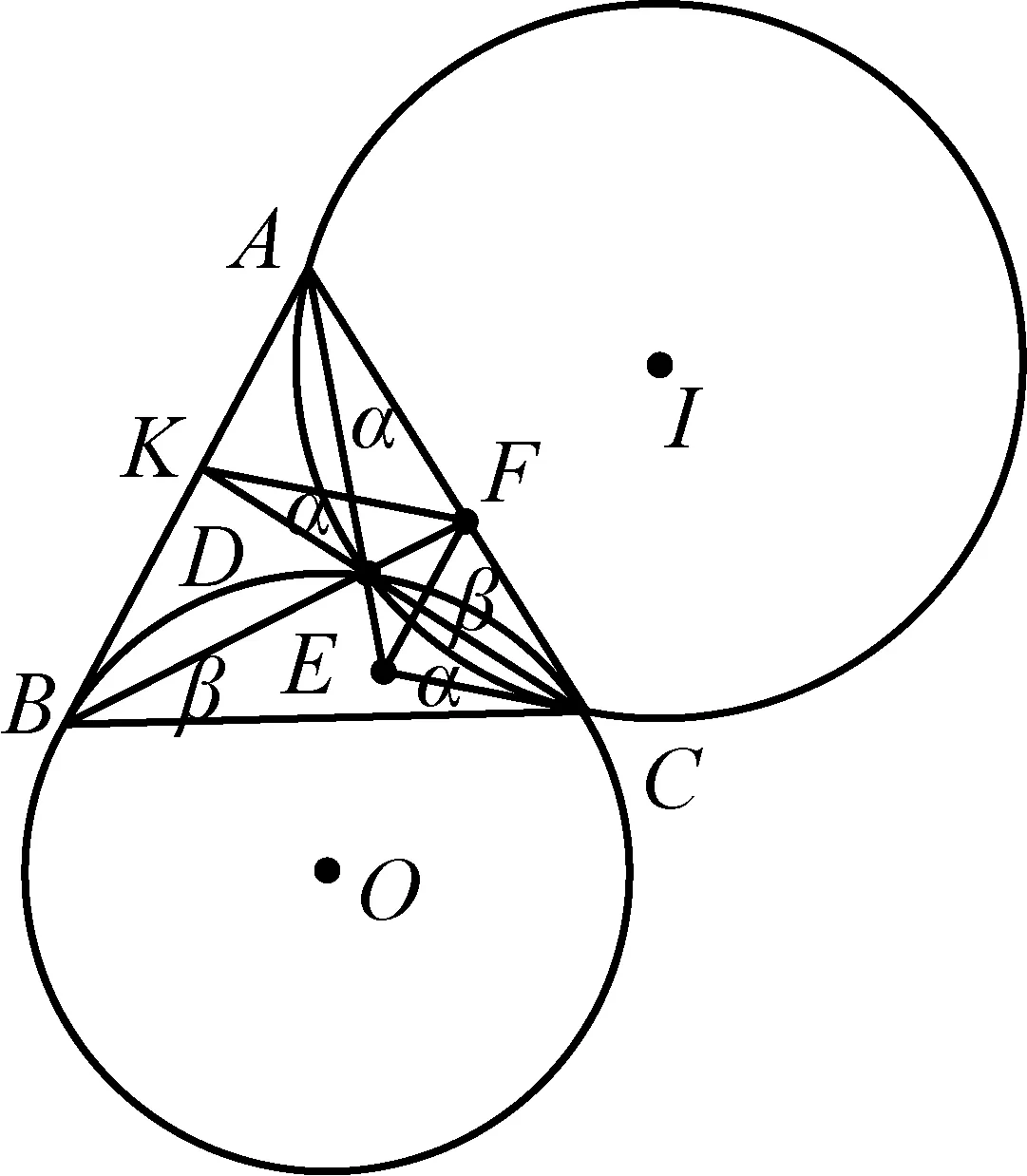
证明延长CD交AB于K,连KF,如图,显然A、K、D、F四点共圆⟹KF∥CE,
设∠DAC=α,
∠DBC=β,
则∠EDC=α+β,
由面积比
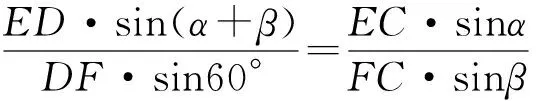
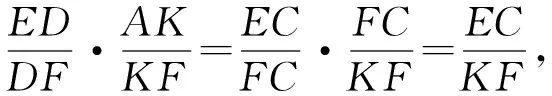

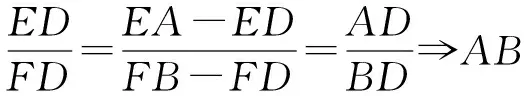
2018年10月问题
(来稿请注明出处——编者)
2446已知实数a满足:有且仅有一个正方形,其四个顶点均在曲线y=x3+ax上,试求该正方形的边长.
(湖北省谷城县第三中学 贺 斌 441700)
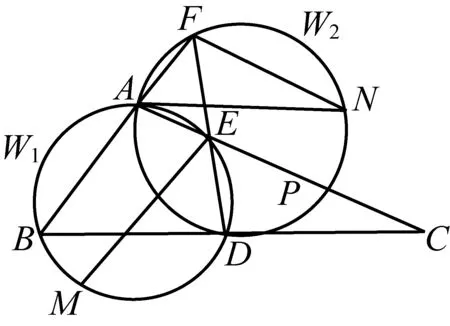
2447如图,已知△ABC的边BC上的中点D,过D的直线交AC和BA的延长线分别于E、F,且AB=EC-AE.过A、D、E三点的⊙W1和过A、D、F三点的⊙W2,.有EM∥BF、FN∥AC,EM、FN分别交⊙W1和⊙W2于M、N.求证:点D是过A、M、N三点圆的圆心.
(江西省高安市石脑二中 王典辉 330818)
2448已知a,b,c,d≥0 满足a+b+c+d=2.求证:
(兰州大学数学与统计学院 冯建波 730000)
2449设a,b,p,q>0,且a+b=p+q=1,求证:
(1)
(河南质量工程职业学院 李永利 467000)
2450如图,AB,AC分别切⊙O于B,C,过A作割线交⊙O于D,E,过D作AB的平行线分别交BC,BE于F,G,求证:F是DG的中点.