维拉尼演讲中的高尔顿板和网页排序

罗艺灵 刘晓曼 保继光

(北京师范大学数学科学学院 100875)

维拉尼(Cedric Villani，1973—)是法国数学家，玻尔兹曼方程的非线性阻尼及收敛于平衡态的证明为他迎来了2010年的菲尔兹奖(Fields Medal).2016年，维拉尼在TED大会*TED是technology，entertainment，design的英文首字母缩写，译为技术、娱乐、设计.TED是美国的一家私有非盈利机构，他们以组织了TED大会而闻名.在TED大会上，各行各业的人都可能站上演讲台，向大众传播他们的想法和创意.演讲，向大众讲述了他对数学的理解，解释了“数学为何如此性感(What’s so sexy about math?)”.

为了向观众展示数学隐藏在我们的整个物质世界中，维拉尼介绍了几个奇妙又贴近生活的数学例子，让非数学工作者也能简单地接受和理解.而作为数学学习者或数学工作者，我们不妨稍微深入地探索其中的高尔顿板和网页排序背后的数学知识.

1 高尔顿板

高尔顿(Francis Galton，1822—1911)是英国科学家、生物统计学家.他是达尔文(Charles Robert Darwin，1809—1882)的表弟，深受达尔文进化论的影响.为了研究遗传现象，他设计了一个钉板，即高尔顿板，利用二项分布的极限是正态分布这一原理，模拟正态分布的性质.

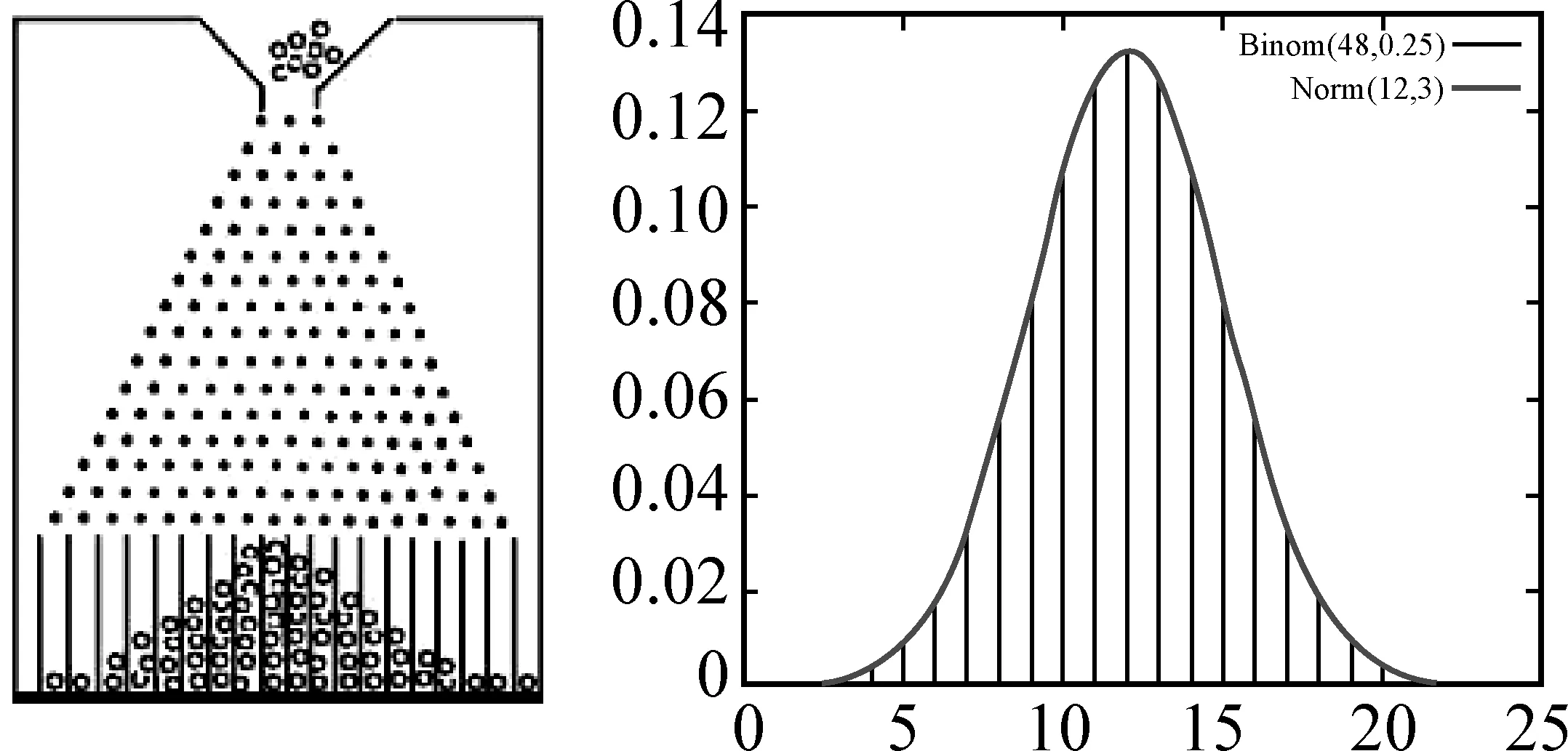
图1

高尔顿板形状如图1，图中的每一个黑点代表的是一颗钉子，每两颗相邻钉子间的距离相等.从入口处放下一颗小玻璃球，它经过多层钉子的空隙，最终落在底部的某个空格中.

考察一个小球落入每个底部空格的概率.观察钉板可以发现，第n行有n+2颗钉子，n+1个空隙，把每一行的空隙从0开始进行编号，第k行即为0，1，…，k个空.

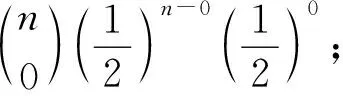
可见，一个小球从高尔顿板下落，落入第k个空的概率是满足二项分布的.因此，足够多的小球通过高尔顿板(行数较多)下落后，堆积而形成的球堆轮廓近似于正态分布的密度函数曲线——高斯曲线.它的发现和发展与著名的德国数学家高斯(Johann Carl Friedrich Gauss，1777—1855)有着密切的联系.

英国物理学家、数学家麦克斯韦(James Clerk Maxwell，1831—1879)基于空间几何的不变性和几个物理上的结论，在1860年发表了论文《气体分子动力学的说明》[1]，导出了气体分子速率分布.它正是一个正态分布.

在介绍麦克斯韦的推导前，先进行符号说明：容器内粒子总数为N；建立空间直角坐标系，将粒子速度v分解到三个坐标轴方向，速度分量分别用符号x、y、z表示；dNx0表示速度分量x处于x0到x0+dx小区间的粒子数目；g(x)代表粒子在分量x方向上的速度分布函数，从而g(x)dx就表示速度分量处于任意值x附近长度为dx的小区间内的概率.

根据各符号代表的含义，以下式子成立：

由于已将速度分解到了三个正交方向上，其任一方向上速度分量的存在和大小不会对其他方向分量的存在和大小产生影响，故三个正交方向上的速度分布是彼此独立的.而三个正交方向在空间上是地位等价的，它们具有相同的速度分布函数.因此，对于另外两个分量，也有类似的公式成立：

从而，粒子速度v的三个分量处于x到x+dx，y到y+dy，z到z+dz区间的概率即是三个独立事件同时发生的概率(其中F表示粒子总体速度分布函数，显然是x、y、z的函数)：

从物理上看，当容器内系统处于平衡态时，容器内各处粒子数密度相同，粒子朝着任何方向运动的概率相等.因此F与粒子速度方向无关，仅是速度大小|v|的函数，从而有等式

(1)

通过求解等式，就可以得知气体分子的速率分布函数了.

首先注意到，若令y=z=0，则有F(|x|)=g(x)g(0)2.x的正负实际上代表着方向，而前文已经说明F与方向无关，即是说F是一个偶函数，F(|x|)=F(x)=g(x)g(0)2.

对等式(1)两边取对数，则可知：

代入等式

经过简单化简，便可知：

=lng(x)+lng(y)+lng(z)，

=lng(x)+lng(y)+lng(z).

等号两边对x求导，即：

从而，

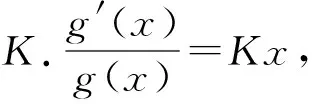
由于粒子速度从-∞到+∞出现的概率应为1，g(x)应当满足：

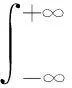
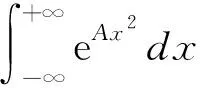
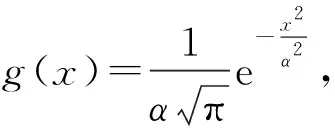
F(v)=F(|v|)=g(x)g(y)g(z)

麦克斯韦在推导的过程中仅用到“所有可能情况的总概率为1”这一个概率知识，借助对气体分子运动的假设和简单空间几何知识，就推导出了气体分子速率分布，而其分布函数恰与正态分布密度函数具有相同的形式.正态分布就像一双自然背后的无形之手，掌控着万物的规律.维拉尼用这个贴近每个人的生活的例子，说明了数学的强大价值.

2 网页排序

维拉尼在演讲中还提到，数学帮助我们超越人类的直觉.他列举了计算机搜索作为一个例子，并以深入浅出的方式说明了其中数学扮演的角色，但数学对网页搜索的帮助并不简单.

互联网中有上百亿个网页，使得网页搜索结果的重复度很高，这给网页搜索带来了极大的挑战.为了应对这一挑战只能对搜索结果进行排序，把用户最有可能需要的网页排在最前面.但问题是：网页的水平千差万别，用户的喜好又不相同，搜索引擎怎么知道哪些网页是用户最可能需要的呢？

在Google主导互联网搜索之前，大多数搜索引擎采用被搜索词语在网页中出现的频数来决定排序.这是有一定道理的，因为用户搜索一个词语，通常表明对该词语感兴趣，既然如此，那该词语在网页中出现次数越多，就越有可能表示该网页是用户所需要的.可是按照这种方法，任何一个翻来覆去倒腾关键词的网页，无论其含金量多低，都会被排在前面.

面对上述问题，1996年初，Google的创始人，当时还是美国斯坦福大学研究生的佩奇(Lawrence Edward Page，1973—)和布林(Sergey Mikhaylovich Brin，1973—)开始对网页排序问题进行研究.在他们看来，网页的排序不能靠每个网页自己来标榜.他们想到了学术界评判学术论文重要性的通用方法，看论文被引用的次数，放在互联网上与论文引用类似的就是网页的链接.那么通过研究网页间的相互链接来确定排序就是PageRank网页排序的思路，网页的PageRank值越大其排序越靠前.具体说就是一个网页被其他网页链接得越多，它的排序就应该越靠前.不仅如此，一个网页越是被排序靠前的网页所链接，它的排序也应该越靠前.

在正式介绍PageRank排序方法前，首先阐述两个相关的概念：

1)网页i的入链：那些指向网页i的来自于其他网页的超链接，通常不包括来自于同一网站内网页的超链接.

2)网页i的出链：那些从网页i指向其他网页的超链接，通常不包括指向同一站点内网页的超链接.

基于上面PageRank网页排序的思路，我们可以知道：

从一个网页指向另一个网页的超链接是PageRank值的隐含式传递，网页的PageRank值是由指向它的所有网页所传递过来的PageRank值总和决定的.这样，网页i的入链越多，它的PageRank值可能就越高.此外，一个网页指向多个其他网页，那么它的PageRank值就会被它指向的多个网页分享.也就是说，即使网页i被一个PageRank值很高的网页j所指向，如果网页j的出链非常多，网页i从网页j得到的PageRank值可能因被稀释也很小.

现在，我们把互联网抽象成一个有向图G=(V,E)，其中V是图的节点集合(一个节点对应一个网页)，E是图的有向边集合(有向边对应超链接).设互联网的网页总数为n(即n=|V|)，上述排序规则可以用数学式子表达：

(2)

其中p(i)表示网页i的PageRank值，Oj是网页j出链的数量，(j,i)∈E表示存在网页j指向网页i的超链接.

若用列向量

P=(p(1)，p(2)，…，p(n))T

表示n个网页的PageRank值，再利用矩阵A表示网页之间的链接关系，并按如下规则为其元素赋值：

例如，下面的网络链接结构图：

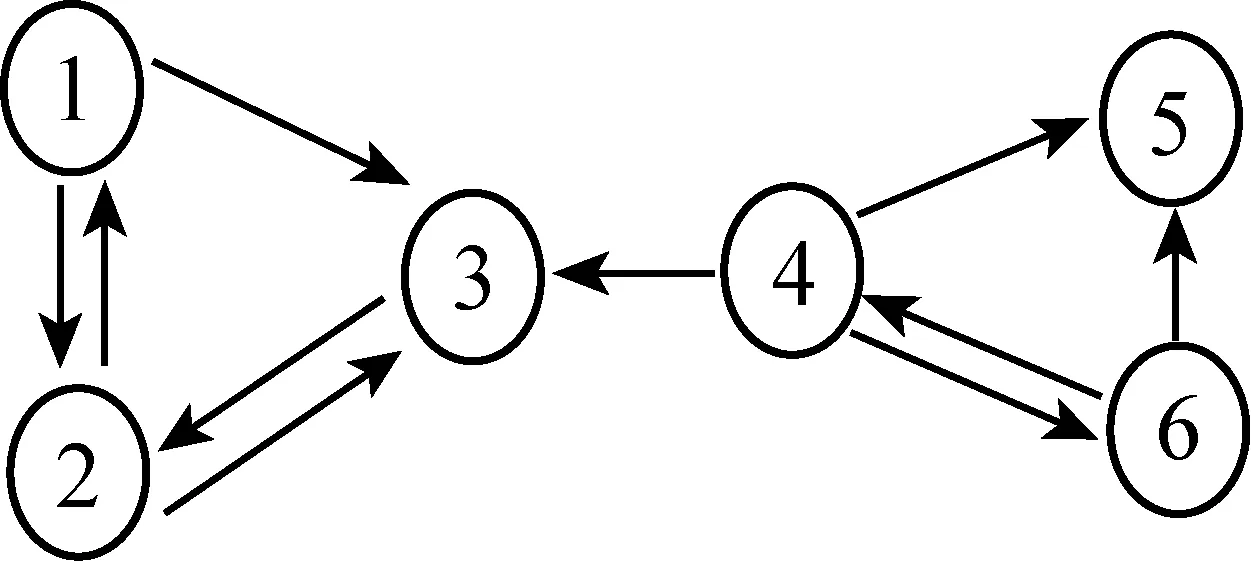
图2

其对应的连接关系矩阵

这样，网页排序的表达式(2)就可以用含n个未知量的线性方程组表达

P=ATP.

(3)

从而要想得到网页排序结果，即在已知矩阵A的条件下，求解向量P，如果从线性代数的角度考虑，这是一个齐次线性方程组，要不只有零解，要不有无穷解.但是由于数据的海量，这给求解过程带来了很多麻烦.

观察方程组(3)，可以发现，如果定义Pn是经过第n次迭代得到的值，给定初值P0，则可以把方程组(3)形式简化如下：

Pn+1=ATPn，n=0,1,2,…(其中P0是给定的)

(4)

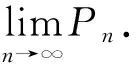
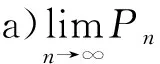
b)如果极限存在，是否和P0的选取无关.

c)如果极限存在并且和P0选取无关，它作为网页排序的依据是否合理？

假设上网浏览下一个页面这一过程与过去浏览的页面没有关系，而仅仅依赖于当前所处的页面，那么上网搜索这一过程可以看作是一个有限状态、离散时间的马氏过程，可用马尔科夫链进行建模，这时P*就可以看成马尔科夫链的一个稳定状态，A可以表示状态转移矩阵，这样就可以转化成马尔科夫链的遍历性和极限分布问题[2].

根据马氏链的遍历性和平稳分布相关定理，若矩阵A是正的、随机矩阵，上面讨论的前两个问题的答案是肯定的.正矩阵即矩阵的每个元素都是正数，随机矩阵则要求矩阵的每一行元素和都为1，且元素都大于等于零.综合两者我们可以知道，要想使得我们研究的问题是肯定的，矩阵A必须满足每个元素是正数，并且每行元素和为1，而上面例子中的网页链接结构图的矩阵就不满足(第5行全部为0)，所以要对矩阵A进行基于现实意义的修正.

第一步，将矩阵A修正为随机矩阵.互联网中那些没有出链的网页，我们称其为悬挂网页，如上面例子中的网页5.当互联网用户访问到悬挂网页时，不可能在这个网页上停止不前，而会自行访问其他网页.对于单个用户来说，自行访问的网页显然与个人的兴趣有关，但是对于无数的互联网用户整体来说，自行访问哪个网页完全是随机的.

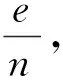
第二步，将随机矩阵S修正为正的随机矩阵.互联网的用户是活生生的人，他们多少都有自己的“性格”，不会完全受当前网页所限，死板地只是访问提供的链接.假定虚拟用户在每一步都有一个小于1的概率a访问当前网页所提供的链接，同时却也有1-a的概率不受那些链接的影响，随机地访问其他的任何网页，由此，矩阵S应当修改为

其中0

n=0,1,2,…，其中P0任意给定.

最后再用迭代求解的算法就可以求出解P*，从而实现排序.

然而上面的一切分析都要通过计算机程序进行实现，GTP0的收敛速度是关系算法是否实用的重要因素，其中a越小，收敛速度越快，但是如果a太小，PageRank网页排序的现实意义将被弱化，佩奇和布林综合实验，考虑了一系列因素后，将a取为0.85.

当然，伴随着科学技术的不断进步，PageRank网页排序算法也得到了不断地发展.随着时间的推进，互联网成为人们生活中不可或缺的工具，网页的数量也在空前的增加，这就带来一个问题，新的网页由于时间问题得不到用户的关注，没有太多的入链，即使网页的质量再高PageRank值反而很低，而那些旧网页由于积累了很多的入链，PageRank值很高，即使内容过时不被用户需要却能排在前面.Timed-PageRank算法为此应运而生.它在PageRank算法基础上增加了一个时间维度，他的思想仍是马氏链，不同之处在于Timed-PageRank不再适用常量阻尼因子，而是引入一个随时间递减的函数来“惩罚”那些过时的网页，使得那些载有新信息高质量的新页面不至于由于入链少而排在后面.除此之外，在前面的叙述中，我们知道PageRank值由一个网页向另一个网页传递时，其值是均匀分配给所有的出链，基于用户反馈的PageRank算法则把从网页i到网页j传递的PageRank值根据用户在网页上停留的时间、页面篇幅、用户正常的阅读速度等进行加权.这样就根据用户的体验对出链所到达的网页质量进行了加权，更能进一步的使得用户最需要的网页排在前面，增加了网页排序的可靠性.

作为当今的数学大师之一，维拉尼对数学的理解，对数学价值的认识超过了许多人.数学不仅能改善人们的生活，还曾改变人类的世界观；数学不仅能帮助人们认识世界，还能协助人们超越人类的直觉，探索未知.数学兼具着美、实用性和无限的商机，它值得所有人去了解和欣赏.

最后，附上维拉尼演讲的网址，供感兴趣的读者欣赏：https://www.ted.com/talks/cedric_villani_what_s_so_sexy_about_math.