基于非线性优划的干道交通信号过渡模型研究

樊友定，姚 佼，严 凌

（上海理工大学管理学院，上海 200093）

0 引言

从流量控制的角度来看，信号过渡通常被理解为从一个信号配时计划转换至另一个信号配时计划的过程，以适应交通需求的变化。在传统的干道协调控制系统中，信号控制方法通常是根据多时段当日时间（Time-of-day,TOD）或交通感应选择控制来设定的。在这两种情况下，信号过渡对干道协调控制交通流的连续性都有负面影响[1]。为了尽可能减小信号切换对车流的中断或扰动，高效的信号过渡方法起到了不可忽视的作用[2]。

传统过渡方法可分为两大类。第1类过渡方法的目标在于使信号过渡持续时间最短。这类方法认为在过渡期间使用非最优控制参数会对交通运行产生破坏性影响，因此试图通过最小化过渡期的持续时间来实现有效的交通运行。Lieberman等[3]提出了快速信号过渡算法，其本质上设计为最小化信号过渡周期的数量和过渡持续时间，然而该过渡方法只适合特定的交通状况。树爱兵等[4]提出了一种基于周期的交通信号协调控制过渡调整策略，能在1～2个周期内完成信号过渡。第2类过渡方法的目标在于使控制参数（如相位差或周期长度等）在过渡期间变化相对较小。这类方法的思路是逐渐过渡到新控制方案，使过渡期间的交通流扰动最小，然而逐渐过渡方法通常会增加车均延误以及需要更多的过渡持续时间。Ross[5]建立网络仿真模型中的交通仿真系统模型（Traffic Simulation System in Network Simulation Model,NETSIM）研究了过渡算法对不同流量条件下平均车速和平均停车次数的影响，并在达拉斯中央高速公路的临街道路系统中进行了验证。在类似的研究中，Basu[6]使用NETSIM和交通网络研究工具模型（Traffic Network Study Tool,TRANSYT）研究了影响信号定时控制计划数量的因素。一些学者研究发现，第2类过渡方法在某种程度上会与第1类使总体过渡时间最小化的方法产生冲突。

对传统过渡方法的评价方面，Nelson等[7]使用硬件在环仿真系统中对干道紧急救援进行了影响分析。该研究采用了计划过渡作为恢复算法，以便在救援终止后重新同步控制器。研究发现，平滑过渡算法使用20%和17%作为最大和最小的周期变化百分比在评估大多数场景下表现得最好，然而实际应用效益并不是很高，且代价高昂。Mussa等[8]利用渐变过渡和线性二次优化技术，将过渡问题建模为一个线性动态过程，寻求目标是协调参数偏差的平方和，例如过渡期间的周期长度和相位差。作者采用了线性二次优化技术来确定最佳转换步数和最佳转换步长。然而，此研究假设了扰动测量值是控制参数的偏差，而不是系统性能，如平均车辆延误等。Shelby等[9],Obenberger等[10],Cohen等[11],Yun等[12]进行了特定交通网络状况下的交通软件仿真分析，得出了相应的结论。栗红强等[13]利用TSIS软件中提出的3种过渡算法并以控制延误作为评估指标，对早高峰前后2种过渡场景进行了研究，发现快速过渡相较平滑过渡具有优越性。卢凯等[14]提出了单周期对称调节过渡和N周期加权调节过渡算法。郭海锋等[15]以各交叉口相位差变化量最小为目标，提出了一种逐步减小新旧协调方案相位差变化量的快速平滑过渡方法。仿真对比分析显示，该方法与传统加法（Add）和减法（Subtract）过渡方法相比具有显著优势。以上学者的研究聚焦于特定交通条件下的过渡方法仿真和对传统过渡方法的改进，虽然实验数据多，但不具有普适性，并且未考虑过渡时期交叉口性能最优化。在已有的优化研究方面，刘慧[16]提出一种基于交通状态预测模型的协调控制方案间的优化过渡方法，并通过VISSIM仿真与快速平滑过渡方法进行对比分析，然而预测模型误差会使得过渡策略适得其反。郑明明等[17]提出一种改进的经验过渡方法，目标是减少在偏移校正和偏移上花费的时间，实验结果证明了最短路径（Shortest-Way）过渡方法优于CORSIM中的短路径（Shortway）过渡方法。由此可见，现状大量研究集中于对现有过渡方法的分析与评估，而不是研究如何提出最优过渡策略。

研究高效稳定的干道过渡策略，以避免传统过渡方法对交通流的扰动、延误以及增加停车次数等负面影响，有比较重要的理论意义和实际应用价值。本文研究了基于延误最小化的信号过渡方法。在阐述本文过渡方法的基本策略的基础上，建立基于非线性优化的过渡模型，并考虑车流离散因素。然后基于改进遗传算法对模型进行求解，并对案例进行仿真，对不同过渡方法进行了对比分析和验证。

1 非线性优化过渡模型

1.1 基本策略

本策略的主要思想在于尽量减少过渡期间的平均车辆延误。因此，要对包括过渡步数和过渡周期步长在内的所有控制变量进行联合优化。在约束搜索空间内，所提出的过渡方法对相位差、周期时长和绿信比进行同步调整。计划过渡方法和传统实时自适应控制算法分别只考虑周期时长和相位差的计算，忽略了过渡期间相位差与系统周期时长间的直接关系。换言之，相位差的逐步改变必须伴随着背景周期时长的特定变化。此外，相对传统过渡方法，本过渡策略放宽了在过渡期内对共同周期时长的要求，可以使过渡更流畅，同时减少不必要的次要道路延误。总而言之，所提出的过渡方法的基本策略在于通过联合约束优化同步调整相位差、周期时长和绿信比来使过渡期间交叉口车辆延误最小。

1.2 模型公式

模型公式的目标函数为过渡期间每个交叉口的平均车辆延误的总和。本文中，《公路容量手册》（Highway Capacity Manual,HCM）[18]中的延迟方程被用来估算平均车辆延误。延误公式包括过渡时期周期时长、绿灯时间、相位差以及各个交叉口的饱和度。

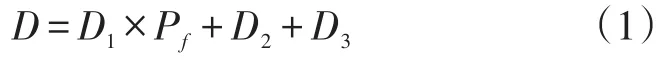
式（1）中：D为车辆控制延误（s）；D1为假设车辆符合均匀到达情形的均匀延误；Pf为均匀控制延误的调整参数；D2为考虑车辆符合随机到达情形以及过饱和排队情况下的增加延误（s）；D3为考虑初始排队情况的车辆初始排队延误（s）。

均匀延误、增加延误、初始排队延误计算公式如下：

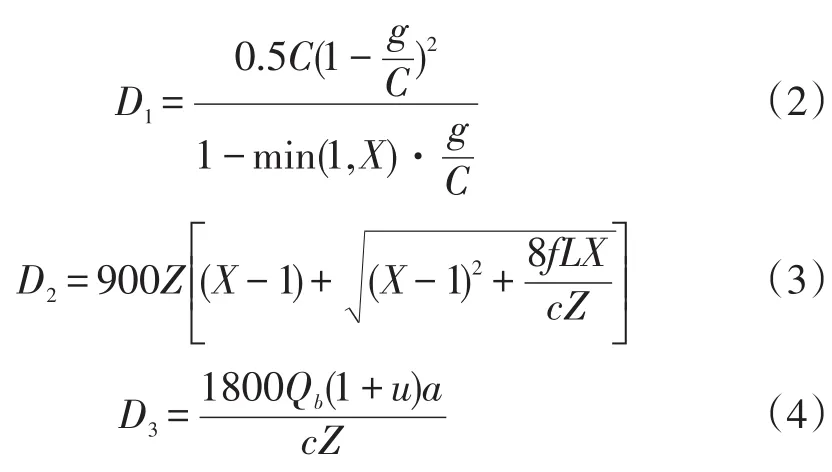
式（2）～式（4）中：g为绿灯时长（s）；C为周期时长（s）；X为交叉口相位关键车流的饱和度；Z为分析时长（s）；f为感应控制的变化系数；L为增量延误修正系数（上游交叉口由于车辆换道引起的）；c为相位关键车流车道组的通行能力（pcu/h）；Qb为车道初始排队车辆数（pcu）；u为排队延误系数；a为分析时长Z内需求大于通行能力的时间（s）；其他参数含义同式（1）。

当然，准确估计下游交叉口的到达模式对于评估协调控制的控制效益至关重要。下游流量到达率是上游车流到达率、上游次要道路流量到达率、上游绿灯时长、下游绿灯时长、周期长度、相位差和路段行驶时间的函数。这个估计的绿灯车辆到达率用HCM公式计算绿信比。因此，在使目标函数最小的情况下，确定候选周期长度、相位差和绿信比。为了符合一般车辆运行规律，采用罗伯逊几何分布来描述车流到达下游交叉口的分布，离散公式如下：

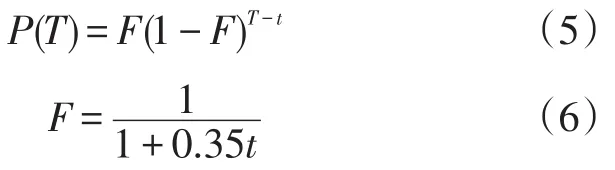
式（5）～式（6）中：P为交叉口之间不同车速行驶时间分布概率；T为交叉口之间行驶时间（s）；t为交叉口之间最小行驶时间（s）。

上游交叉口与下游交叉口相位差期望值计算方法如下：

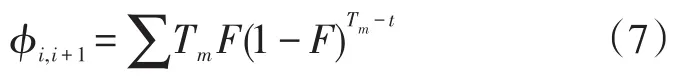
式（7）中：ϕi,i+1为相邻交叉口相位差（s）；Tm为不同行驶时间（s）。

由上游交叉口到达下游交叉口的车流到达率计算方法如下：

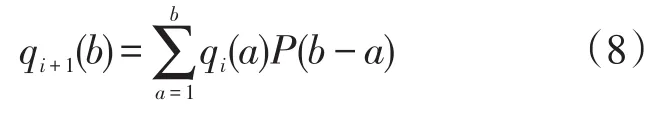
式（8）中：qi+1(b)为第b时段到达下游交叉口停车线断面的车流率；qi(a)为第a时段驶离上游断面的车流流率；P(b-a)为从上游停车线到达下游断面行驶时间为b-a的概率分布函数。

式（7）和式（8）是求式（9）中自变量相位差与流量的方法。本文所提出的非线性优化过渡模型如下：

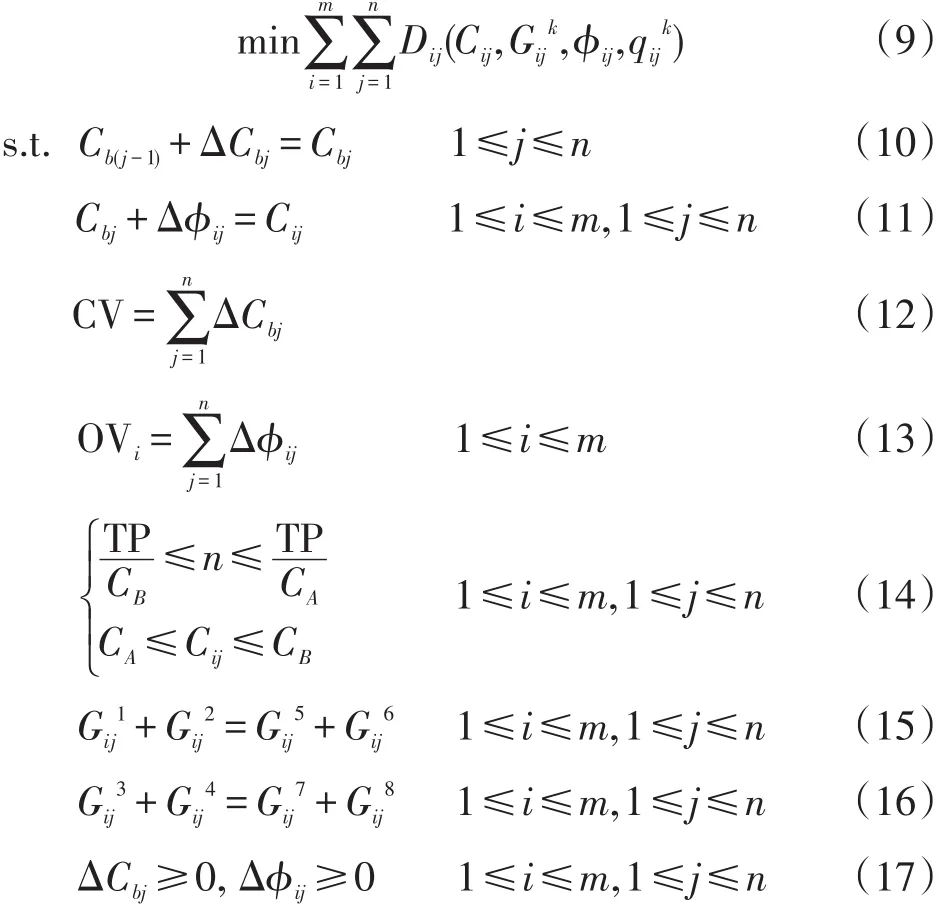
式（9）～式（17）中：i为第i交叉口；j为第j过渡步骤；k为第k相位；n为总过渡周期个数；m为干道协调交叉口总数；Cij为第i交叉口在第j过渡时期过渡周期时长（s）；ϕij为第i交叉口在第j过渡时期相位差（s）；Gij k为第i交叉口在第j过渡时期第k相位的绿灯时长（s）；qij k为第i交叉口在第j过渡时期第k相位的交通流量（pcu）；Dij为第i交叉口在第j过渡时期的车均延误（s）；Cbj为第j过渡时期的背景周期时长（s）；ΔCbj为第j过渡时期周期时长变化量（s）；Δϕij为第i交叉口在第j过渡时期相位差变化量（s）；CA为信号定时计划的当前周期长度（s）；CB为信号定时计划的下一个周期长度（s）；CV为过渡期间周期时长变化总量（s）；OVi为第i交叉口在过渡期间的交叉口相位差变化总量（s）；TP为过渡总持续时间（s）。

本文所提出的过渡模型作为一个非线性优化模型，包括3个控制过渡过程的重要决策变量。第一个决策变量是过渡周期的个数n（即在过渡时期内需要多少个周期才能有效完成信号过渡）。第二个决策变量是过渡步长ΔCbj。这两个变量用于计算背景周期时长Cbj，这是用于干道协调控制的常用周期长度。通过使用过渡周期个数和过渡步长，可以对协调干道进行逐步循环过渡，该协调干道由下面提出的模型公式的第一个约束方程建模。相位最小绿灯时长为用户定义的约束，周期长度约束在优化模型中是隐含的。最后，第3个关键决策变量是在每个过渡步骤中每个交叉口调整的相位差变化量Δϕij。因此，可以通过将相位差变化与背景周期时长相加来确定单个交叉口的周期时长，该背景周期时长计算方法是所提出的模型公式的第二约束方程（式（11））。式（12）和（13）是第三和第四个约束方程，分别表示在过渡时期的周期和相位差总变化的守恒性。此外，过渡周期的数量应通过过渡总持续时间TP和过渡期前后干道协调控制两个背景周期时长（式（14））确定。为了更好地实现干道控制，在过渡期间每个交叉口进行独立的相位差变化。因此，如果此结果对过渡模型目标函数有有利影响，则特定交叉口可能比其他交叉口更早完成自己的信号过渡。当前周期长度和相位差从相位差变化的约束值解码并和流量以及绿色时间的约束值一同输入车辆延误目标函数。

1.3 算法求解

复杂和大规模的数学问题（如信号时序优化）的一个根本问题是如何有效地达到全局最优解（如果存在）或接近最优解。遗传算法是求解这类复杂模型的一类颇具吸引力的算法。

在过渡步骤j中，过渡周期应小于过渡总时长的剩余量。此外，在此过渡步骤中，应确定每个交叉口的最小相位差变化，因为过渡步骤中的交叉口周期长度应小于或等于模型公式中所述的新计划周期时长。否则，通过在后面的过渡步骤中将过渡的相位差变化量添加到背景周期中，单个交叉点的周期时长可能大于新计划周期时长。因此，应通过从过渡总时间的剩余量中减去相位差变化的最小量来决定最大步长。在这种情况下，应该从具有最大相位差残差的交叉口中选择相位差过渡的最小量，以便满足此步骤中所有交叉口的周期时长约束。过渡步骤j处的周期变化的边界如下：

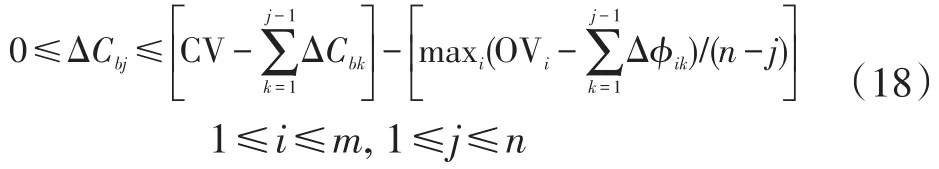
可以由方程（19）确定过渡步骤j中交叉口i的相位差变化边界。此步骤中的相位差变化量应小于或等于总相位差变化量的剩余量。此外，它应该满足周期时长约束，因此它应该小于或等于周期时长变化总量的剩余量。另一方面，可以通过执行剩余步骤可用的最大相位差变化量确定此步骤中的最小相位差变化量。也就是说，最小相位差变化量等于总相位差变化量的剩余量减去残余步长的最大相位差变化量。过渡步骤j中交叉口i的相位差变化边界如下：

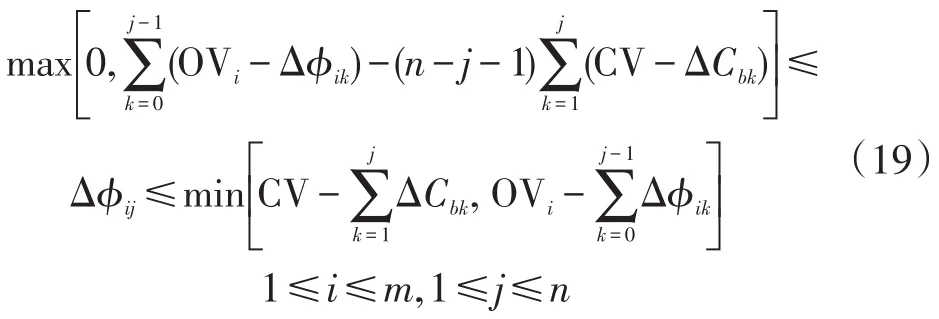
使用上述边界条件，可以按下式进行周期变化和相位差变化的解码处理：

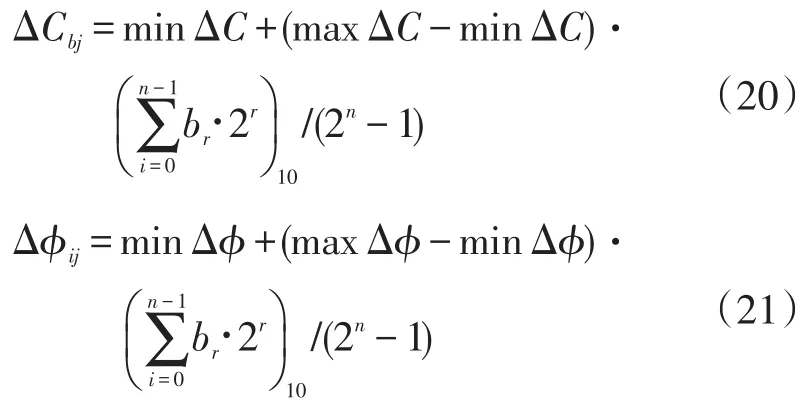
式（20）～式（21）中：minΔC为最小周期变化量（s）；maxΔC为最大周期变化量（s）； minΔϕ为最小相位差变化量（s）；maxΔϕ为最大相位差变化量（s）；n为二进制字符串中使用的位数；br为第r位数值（0或1）。

一旦通过上述解码过程确定了周期变化和相位差变化量，就可以计算出各个交叉口的周期时长和相位差量，因为两者都已经通过当前信号定时计划已知，并且周期时长也用于计算相位绿信比，计算方法如下：

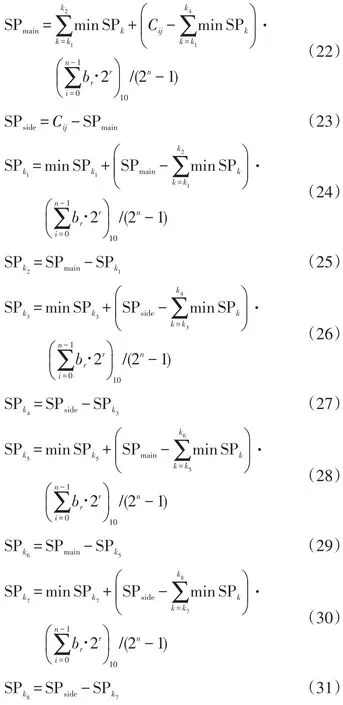
式（22）～式（31）中：Cij为第i交叉口在第j过渡时期过渡周期时长（s）；SPmain为主要道路绿信比时间（s）；SPside为次要道路绿信比时间（s）；SPk为第k相位的分配时长，k=k1,k2,…,k8；minSPk为第k相位最小分配时长（s）；n为二进制字符串中使用的位数；br为第r位数值（0或1）。

以相同的方式，通过使用上限和下限边界条件简单地进行相位绿信比的解码。一旦通过上述解码过程确定了控制参数，基于遗传算法的优化模块借助Matlab优化工具箱（Optimization Toolbox）求解HCM延迟等式，计算所选有机体的适应度。由于每个交叉口需要优化迭代的代数不同，有的收敛快，有的慢，为了使得每个交叉口计算优化时间一致且提高计算效率，所以遗传算法不是建立收敛标准，而是在所有情况下运行100代。基于遗传算法的优化过程中使用的控制参数如下：（1）适应度值：车均控制延误；（2）种群规模：200；（3）选择机制：二进制比赛选择；（4）遗传操作：均匀交叉；（5）交叉概率：0.75；（6）变异概率：0.03；（7）迭代代数：100。

2 案例分析

本文以常州市和平路沿线三交叉口（清凉路、光华路和吴中大道）干道协调控制为研究对象，交叉口间距分别为860m和400m，如图1所示。过渡时段为平峰向高峰过渡，新旧方案配时计划已根据流量进行了优化设计。为了体现过渡时期内车流变化的形式，本文采用3种不同流量增长模式来校验模型，分别为线性、指数和对数流量输入[19]。

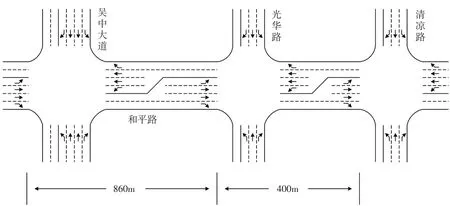
图1 干道交叉口示意图

仿真环境采用Visual C++调用VISSIM内部COM接口，对MATLAB求解方案进行仿真分析，并且与经典的两周期、三周期等过渡方案进行对比分析。

现状3个协调控制交叉口平峰时期与高峰时期公共周期分别为120s,140s。平峰时期清凉路、光华路和吴中大道相对背景交叉口相位差分别为：19s,85s,1s。高峰时期清凉路、光华路和吴中大道相对背景交叉口相位差分别为：48s,125s,29s。总相位差变化量分别为：29s,40s,28s。仿真时长取15min，仿真结果如表1～表3，图2～图4所示。

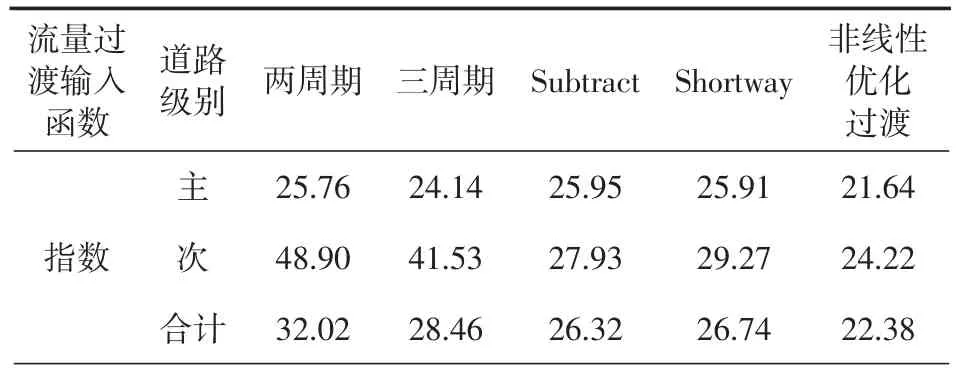
表1 和平路—吴中大道不同过渡方法车均延误（单位：pcu/s）

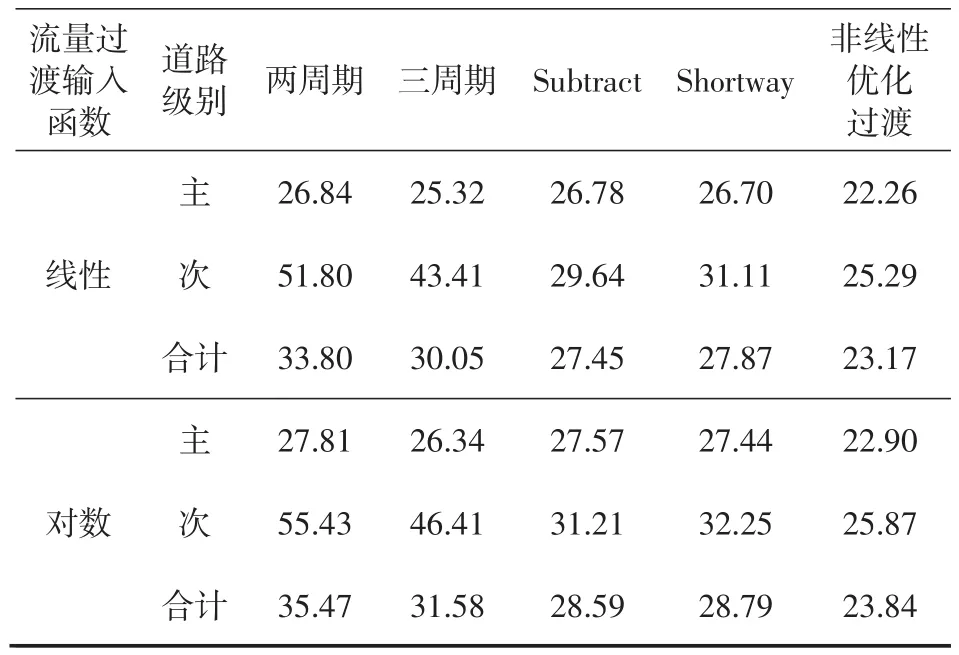
表1（续）

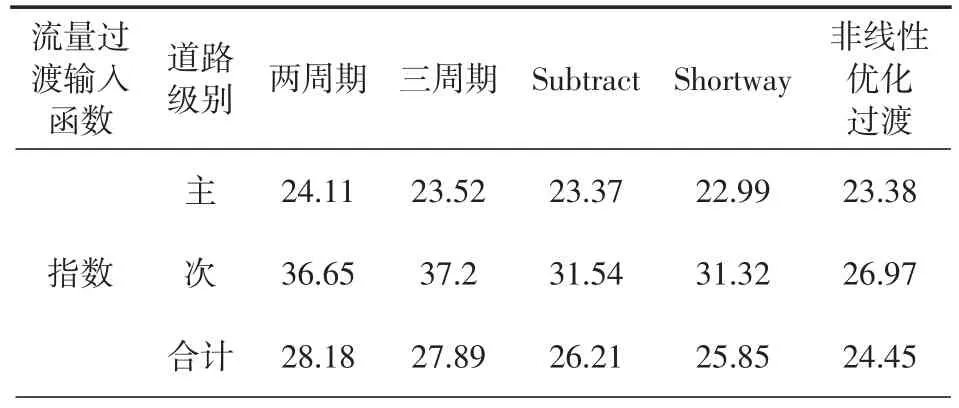
表2 和平路—光华路不同过渡方法车均延误（单位：pcu/s）

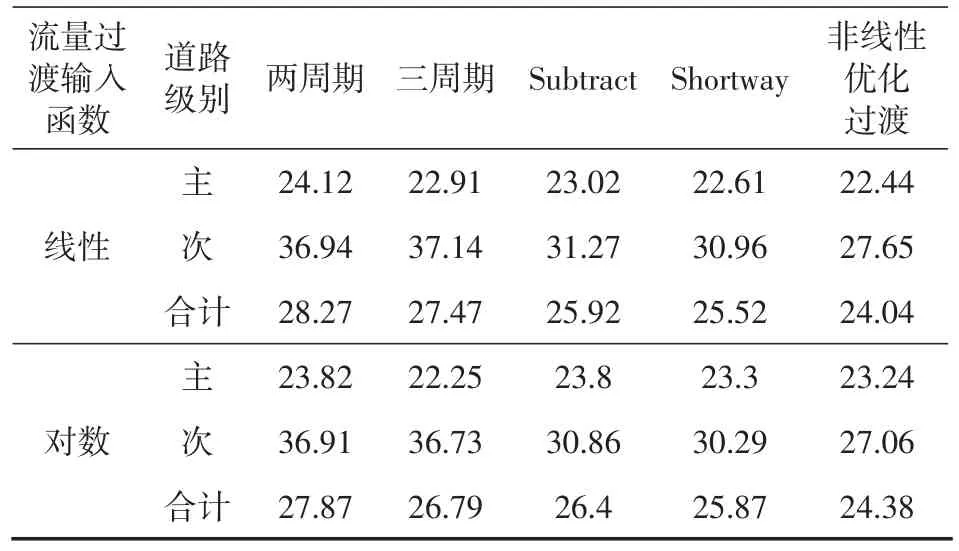
表2（续）

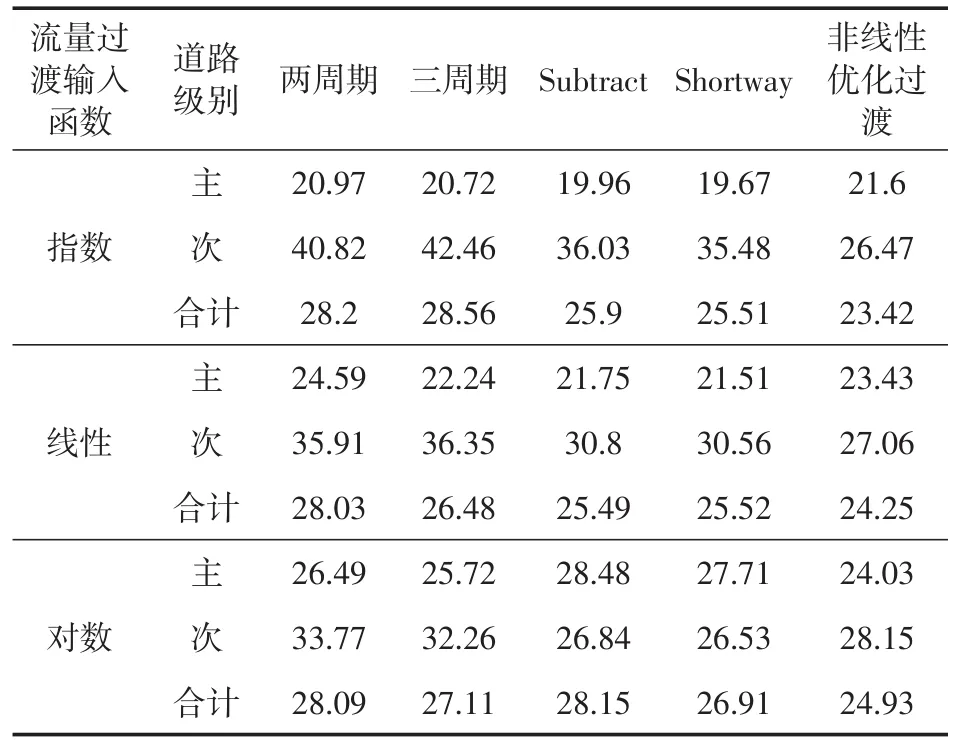
表3 和平路—清凉路不同过渡方法车均延误（单位：pcu/s）

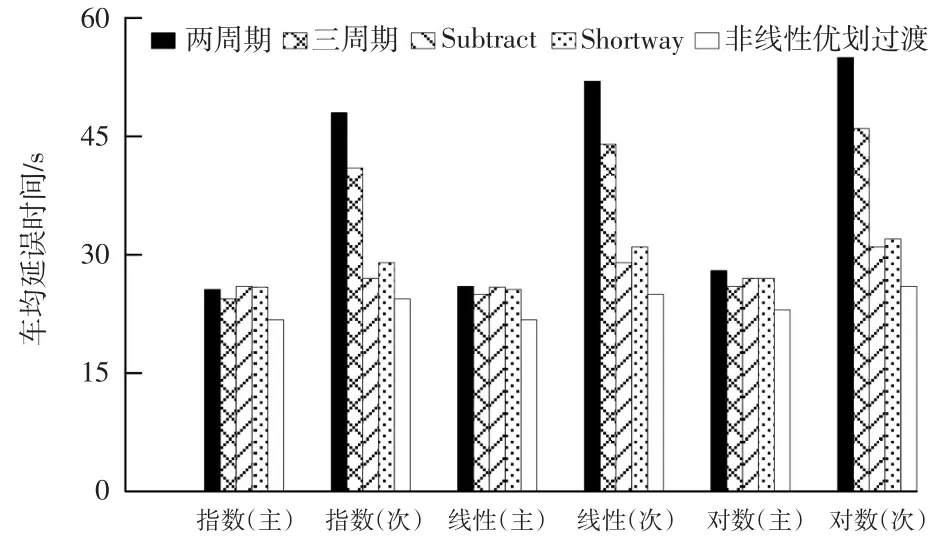
图2 和平路—吴中大道不同过渡方法车均延误

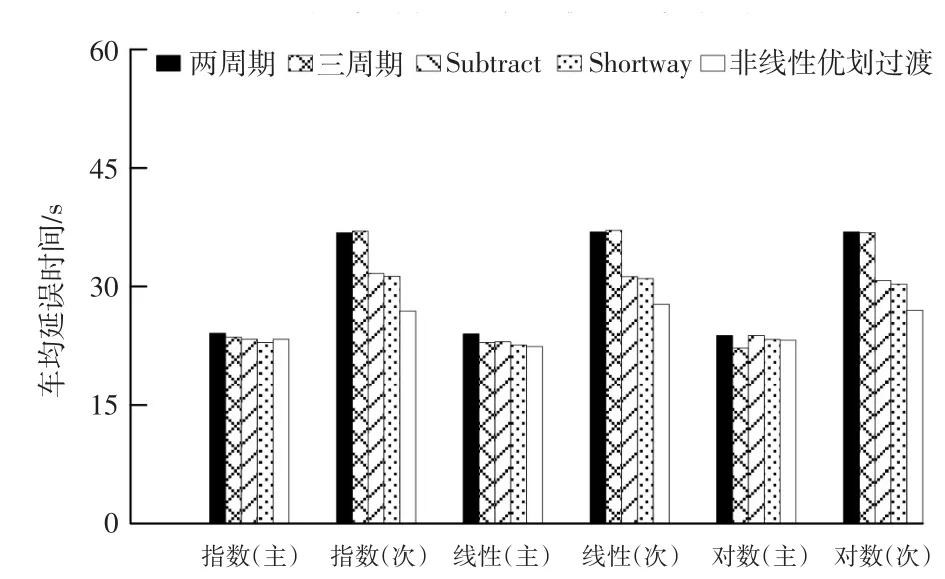
图3 和平路—光华路不同过渡方法车均延误

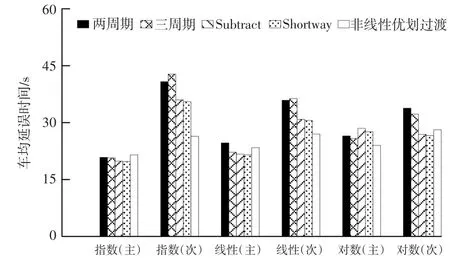
图4 和平路—清凉路不同过渡方法车均延误

对仿真结果进行分析可得出以下结论：（1）非线性优化过渡模型整体表现具有一定优势。在延误性能方面，相较于两周期、三周期、Subtract、Shortway，非线性优划过渡模型指数流量输入时分别提高了20.1%,17.2%,10.4%,10%；线性流量输入时分别提高了20%,14.6%,9.2%,9.2%；对数流量输入时分别提高了18.9%,13.8%,11.9%,10.1%。（2）传统过渡方法多数以牺牲次要道路车均延误来提高主要道路延误性能，而非线性优划过渡模型对主次道路延误都进行了优化，为次要道路保留了足够的绿灯时间。（3）传统过渡方法中，Shortway过渡方法在主次道路延误方面表现最好。（4）两周期和三周期过渡方法以牺牲次要道路延误时间提升主要道路性能进行交通方案过渡。

3 结论

本文通过建立过渡期间基于车辆总延误最小的非线性优划约束模型，求得过渡期间最优过渡周期个数、最佳过渡步长以及各交叉口最优相位差变化量，通过联合优化使得交叉口在过渡期间达到最优性能。通过对案例的仿真对比分析可知，所提出的过渡模型在大范围交通条件下与传统过渡方法相比具有明显优势，在减少车均延误的同时，也保证了干道最宽绿波带。然而本文仅以过渡时期延误为目标，未考虑其他控制目标，比如排队长度、最大通行能力等。所研究的干道协调控制背景周期时长相同，而实际控制中存在有的交叉口控制周期为双周期的情况，所以未来的研究需要从这些方面入手。