智能交通对城市交通效率改进的贡献——基于匹配和双重差分模型的估计

陈建华，刘学勇，刘 娜

（交通运输部科学研究院，北京 100029）

0 引言

信息化是推动交通运输行业不断转型升级的重要动力，信息技术的不断发展也为城市交通运行改善带来新的契机。近年来，信息化和随之而来的智能交通发展已经深刻改变了城市交通传统运行模式。智能交通建设在改善城市交通运行方面的作用明显，特别是在缓解城市交通拥堵、提高城市交通运行效率方面发挥了重要作用[1]。不同学者在探索利用不同的方式来定量评价智能交通建设对交通发展的贡献。李腾海子从宏观的角度，研究提出城市交通信息化评价指标体系，测度城市交通信息化发展水平，并以柯布-道格拉斯生产函数法为基础构建贡献率模型，测度交通信息化对城市交通运输业产值的贡献率，最后以北京市为例进行了实证分析[2]。董璐等则从相对微观的角度，研究提出应用数据包络分析（Data Envelopment Analysis,DEA）方法，结合回归分析，从投入产出角度选取指标建立模型，测算和评价了交通信息化对道路畅通性改善的贡献。其研究结果显示，北京市2005—2014年交通信息化对道路畅通性改善的年平均贡献值为17.47%[3]。吴利霞等通过分析智能交通系统（Intelligent Transportation System,ITS）项目实施的特点与双重差分模型应用的相似性，将ITS项目实施作为外生政策变量，基于改进的双重差分模型，结合主成分分析法测算了智能交通系统项目对广州城市交通畅通性的净贡献率[4]。关淑琪等尝试运用双重差分的核心思想，结合聚类分析，采用分位数回归，解决了内生性、控制组受影响的问题，从影响武汉交通畅通性的众多因素中，剥离出不停车电子收费系统（Electronic Toll Collection,ETC）的净贡献[5]。

从国外现有研究来看，专门定量研究智能交通建设对于交通效率提升贡献的不多，但是对于公共政策的影响和贡献评价的研究则相对较为成熟，这也是本项研究中重点借鉴的核心思想。Heckman和Ichimura等利用不同的匹配算法，融合了实验数据和实际数据，对一项职业培训项目的效果进行了评价[6]。Heckman和Lozano在差分模型的基础上，利用匹配算法，通过控制变量来评估经济模型选择的影响[7]。Chay等则对匹配算法中的得分计算方法做了改进[8]。

从现有的研究来看，主要存在的问题：一是无法真实模拟同一评估对象在智能交通项目实施前后其城市交通和经济社会发展状况；二是难以真正从众多影响因素中单独剥离出智能交通项目建设对城市交通运行效率改善的净贡献。基于以上考虑，笔者借鉴国内外关于公共政策贡献评价的思路，采用“自然科学实验”的理念，为评价城市构造对照城市，引入双重差分和倾向得分匹配模型，以系统建设之后（时刻）和之前（时刻）的评价城市和对照城市各自的畅通性指标差值再次作差，量化评价智能交通项目建设应用效果对城市交通运行效率改善的贡献率。

1 基于匹配和双重差分模型的提出

Heckman（1985，1986）最早提出了双重差分（Difference-in-difference,DID）模型，也就是利用外生公共政策所带来的横向单位（Cross-sectional）和时间序列（Time-series）的双重差异来识别公共政策的处理效应（Treatment Effect）。其核心思想是：将政策实施类比于自然科学实验（Natural Experiment），将受到政策影响的社会群体归为实验组（Treatment Group），将没有受到政策影响的社会群体归为控制组（Control Group），在分别计算实验组和控制组各组在政策实施前后差异（Δy1和Δy2）的基础上，再比较两个差异的差值(Δy=Δy1-Δy2)，以获知政策实施所产生的净效应[9]。

双重差分模型的基本思路如表1所示。

表1 双重差分模型

双重差分估计的主要思路是：利用一个外生的公共政策所带来的横向单位和时间序列的双重差异来识别公共政策的处理效应。尽管双重差分模型允许个体存在不可观测的因素，并且能捕捉到实验组与对照组的政策差异，但双重差分模型中对照组的选取过于主观，缺乏定量的标准。因此，笔者在研究过程中，考虑在传统双重差分模型的基础上引入匹配算法。通过匹配的形式，在一个大范围内寻求最优化的对照组，消除非共同支撑域和非同分布所导致的估计偏差，一定程度上可以避免对照组选取的主观性。因此，本项研究中尝试将倾向得分匹配引入到传统的双重差分模型中，搭建起基于匹配和双重差分的模型（Matching Difference-In-Difference,MDID），以便更加客观地度量智能交通项目建设对城市交通运行改善的净贡献[10]。

2 模型设计及结果分析

2.1 建模分析的主要步骤

第一步：对影响城市交通运行效果的因素及表征指标进行分析，选择表征城市交通运行效率的核心指标，对影响核心指标的经济社会变量指标进行相关性分析，初步筛选出模型初选变量指标集。

第二步：根据影响因素分析结果，按照被解释变量、解释变量、控制变量对变量进行分类分组，在此基础上对变量进行相关性检验，重点筛除弱相关或者自相关变量。

第三步：利用匹配模型算法，针对被评估城市，选择构建备选城市的匹配资源池。

第四步：采集对照匹配城市基础数据，建立分析模型。

第五步：对模型进行回归估计，并对估计结果进行分析。

2.2 城市交通运行影响因素分析

影响城市交通运行效果的因素主要有两个：一是交通需求，二是交通供给。交通需求主要取决于城市用地及布局、经济社会发展以及机动车保有量等三个因素[11]。其中，城市用地及布局直接决定城市交通出行的空间分布，包括出行方向、出行距离以及以通勤交通为主的城市交通的出行强度。经济社会发展则决定了城市交通出行总量需求。城市人口越多、经济越发达，出行需求就越大，即交通出行总量就越大。机动车保有量则直接决定机动化出行需求，且这部分需求直接作用于城市路网，直接决定城市道路交通或畅通或拥堵的状态。交通供给则主要服务于车辆运行，包括道路里程、道路面积、路网结构、停车场地等基础设施，公共交通、轨道交通、出租、自行车等出行方式的运力配备，以及智能交通管理系统、出行信息发布系统等信息化系统建设等。由于受建设周期、建设资金以及城市空间范围的限制，与交通需求的快速增长相比，交通供给能力的增长则相对较缓，一定程度上也加剧了交通供需之间的矛盾。

为了更加科学客观地描述城市交通运行改善与相关影响因素的关联关系，利用数据定量分析人口、地区生产总值、机动车保有量等影响因素与城市交通运行指标之间的关系。在实际评价过程中，考虑选用城市路网平均运行车速作为城市交通畅通性表征指标。考虑到2010年，研究对象广州市的城市智能交通项目建设发展较快，笔者以2010年为对照基年，并依托Wind数据库和我国交通运输部《城市（县城）客运交通统计（年报）》，采集了包括北京市在内的36个城市2008—2012年的路网平均运行车速、地区生产总值、常住人口数、民用汽车拥有量、道路里程、道路面积、公共电汽车运营车辆数、公交运营里程以及公共电汽车客运量等数据。利用Eviews软件进行相关性检验，结果显示，地区生产总值、常住人口、民用汽车拥有量、道路里程、道路面积、公共电汽车运营车辆数、公交运营里程和公共电汽车客运量等8个影响因素与路网平均运行车速之间的相关系数均在0.7以上，相关性较高。

2.3 MDID模型的构建与计算

（1）变量分类与筛选

根据“从一般到简单”的计量建模原则，在搭建最初模型基准时应考虑尽可能多的变量，然后根据计量结果进行逐步剔除。根据各因素性质和作用，进行被解释变量、解释变量以及控制变量的归类，结果如下：

①被解释变量：路网平均运行车速。

②解释变量：民用汽车拥有量、道路里程、道路面积、公共电汽车运营车辆数、公交运营里程和公共电汽车客运量。

③控制变量：常住人口、地区生产总值。

MDID模型的一个重要假设是条件独立假设，即要求自变量被“干预”所影响，但不能影响“干预”[12]。本研究中针对不满足独立假设条件的变量剔除过程如图1所示。

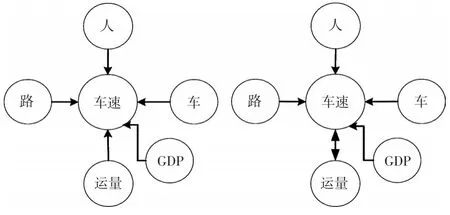
图1 剔除不满足独立假设条件的变量示意图

格兰杰因果检验结果表明，运量为车速的格兰杰因果检验结果是显著的，即运量是车速的格兰杰因，运量不适宜作为车速的自变量。再对以上变量进行Probit稳健回归，回归检验结果如表2所示。

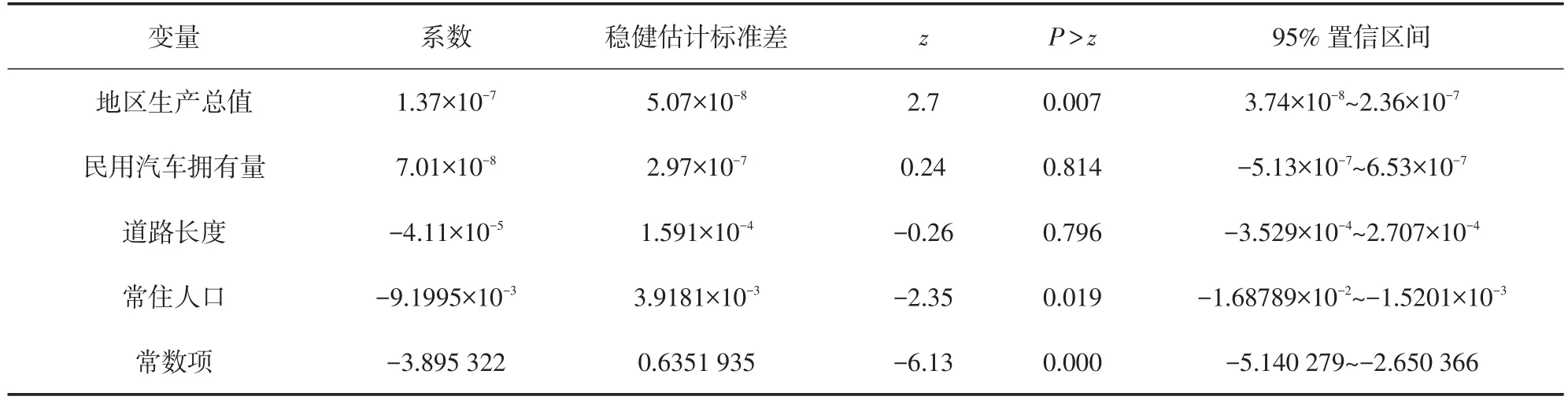
表2 Probit稳健回归结果

从检验结果来看，公交车辆数、公交运营里程这两组数据，在匹配的Probit回归过程中，系数稳健检验并不显著，并且公交公里数和民用车辆数存在较高的共线性，公交运营里程和道路里程也存在较高的共线性，因此不适于进入模型[13]。此外，道路长度和道路面积这两个指标内部强相关，不适于同时用于模型中，考虑仅保留道路长度指标。因此，在后续的模型评估分析中着重考虑地区生产总值、民用汽车拥有量、道路长度、常住人口作为主要变量。

（2）匹配池的构建

双重差分需要对城市进行对比评价。理论上，作为与考察城市对比的控制组备选城市，只需选取不受政策影响即未参与示范工程的城市即可。但实际操作中，选取多个对比城市进行加权后匹配倾向得分，优于仅仅单个对比城市的匹配倾向得分。因此，本项研究中希望通过在更大范围内，研究筛选出一些可比照的城市，建立一个较大尺度范围的初始“匹配池”，然后基于初始匹配池进行匹配，选择最优的对照组成员。因此，在确定最终的对照组城市之前，首先需要选择确定哪些城市进入初始“匹配池”。根据模型基本假设条件和原理，实施的信息化项目仅影响考察城市而不影响选取的对比城市（控制组），或者影响可以忽略。因此，作为对照组的城市必须满足以下几个要求[14]：

①模型允许存在不可观测因素的影响，但假定它们是不随时间变化的，即可以存在个体固定效应。固定效应的要求蕴涵着不随时间变化的不可观测因素，考虑极端的情况，选取某村作为对比城市，由于后者波动明显快于前者，必然造成不符合固定效应假设。

②如果有未被观测到的与被解释变量相关的因素，同时影响到是否进行物联网示范工程的实施，则说明控制组和实验组并非随机选取，并非“自然实验”，不满足假设。反过来讲，就是指除政策影响外，其余因素影响相同。理论上，假设城市规模属于不可观测的因素，并且与被解释变量（平均车速）相关，那么城市规模越大的城市越倾向于实施需要较大资金规模和较高技术要求的城市智能交通项目。

③个体异质性不存在非球形干扰，或经过“处理”后不存在。

④控制组和实验组的特征稳定。

从假设条件来看，城市规模差异过大会出现问题，意味着城市规模的差异不应该作为未观测因素的构成部分[15]。根据以上要求，结合中国的行政区划，一个可行的方案是考虑选用36个中心城市作为匹配池，另外再选择全国36个地级以上设市城市作为匹配备选库。此外，考虑到个别城市数据的离群特征，采用苏州代替拉萨作为备选城市入选。

MDID模型要求的截面数据为政策实施前，因此选择以上36个城市2010年的数据作为数据备选库截面数据。计算各城市的得分倾向值，具体结果见表3。

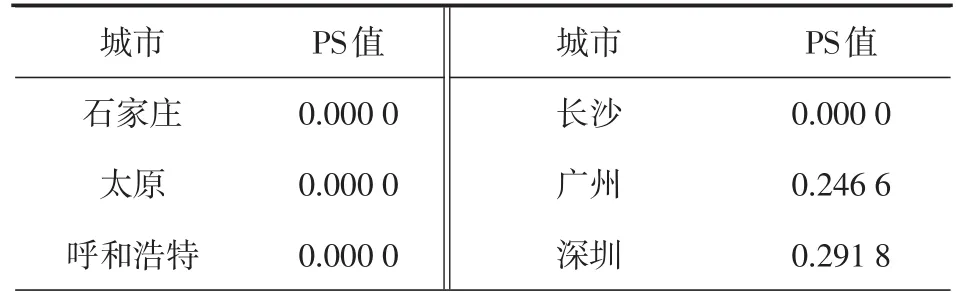
表3 各城市得分倾向值

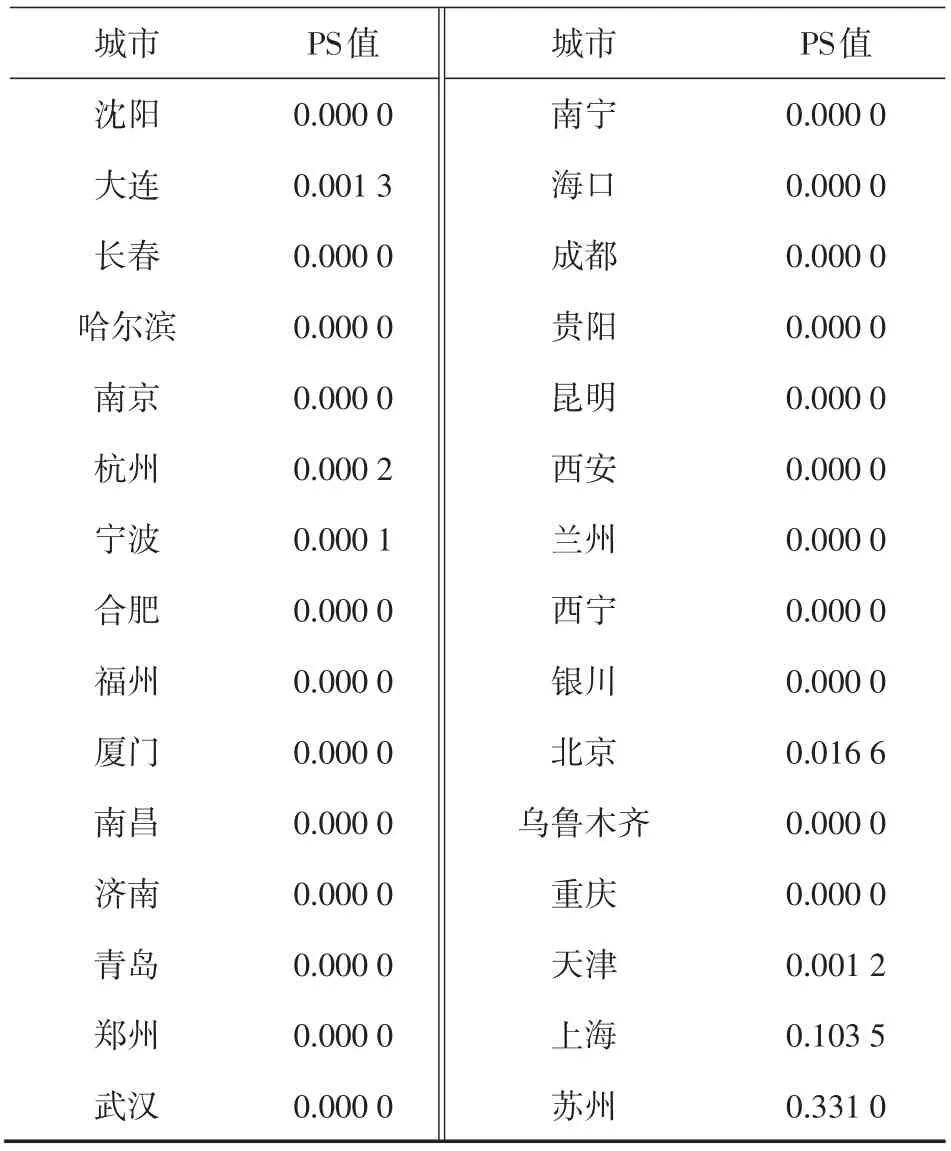
表3（续）

经过计算，在对照组36个城市中，深圳、上海、苏州的倾向得分与考察样本城市广州的匹配度较高。因此，考虑将苏州、上海、深圳共同列为匹配对照组备选城市。再利用高斯核密度函数[16]分别计算这3个对照组城市的得分权重，权重计算结果如表4所示。

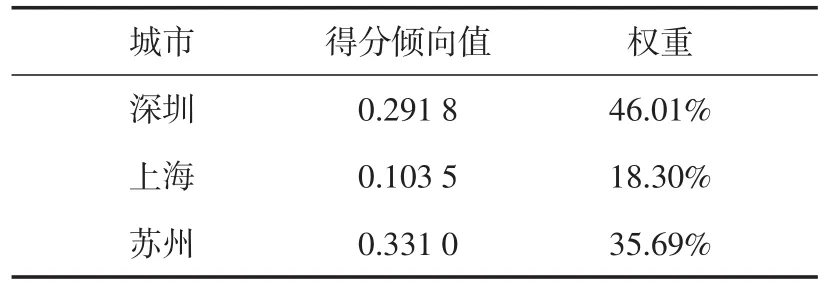
表4 对照城市权重

（3）模型估计及计算

贡献率是因解释变量变动引起的被解释变量变动除以总的被解释变量变动。比照索洛增长模型，取对数差分以后，虚拟变量系数可以理解为就是贡献率。设计组别虚拟变量（grp）、政策虚拟变量（its）、交叉项（grp×its），按照城市进行面板分类，建立的最终模型如下。

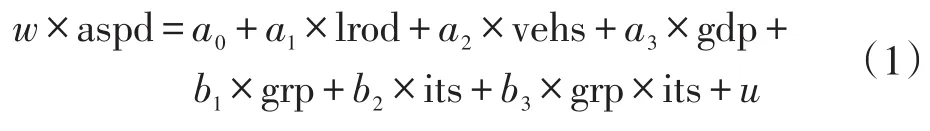
式中：w为贡献率；aspd表示平均车速，为决策变量；vehs表示民用车辆数，为解释变量；lrod表示道路长度，为控制变量；gdp表示地区生产总值，为控制变量；its为政策变量，tit=0表示智能交通项目建设前的区段（2008—2010年），tit=1表示智能交通项目建设后的区段（2011—2012年）；grp为组别变量，dit=0表示控制组对象，dit=1表示实验组对象；a0,a1,a2,a3,b1,b2,b3,u为回归系数。

采集对照组城市相关基础数据，利用固定效应估计模型，采用最小二乘法进行估计[17]。计算求解后，被考察样本城市信息化项目对城市交通运输改善的贡献约为9.2%。模型系数和方差的估计和检验结果见表5。

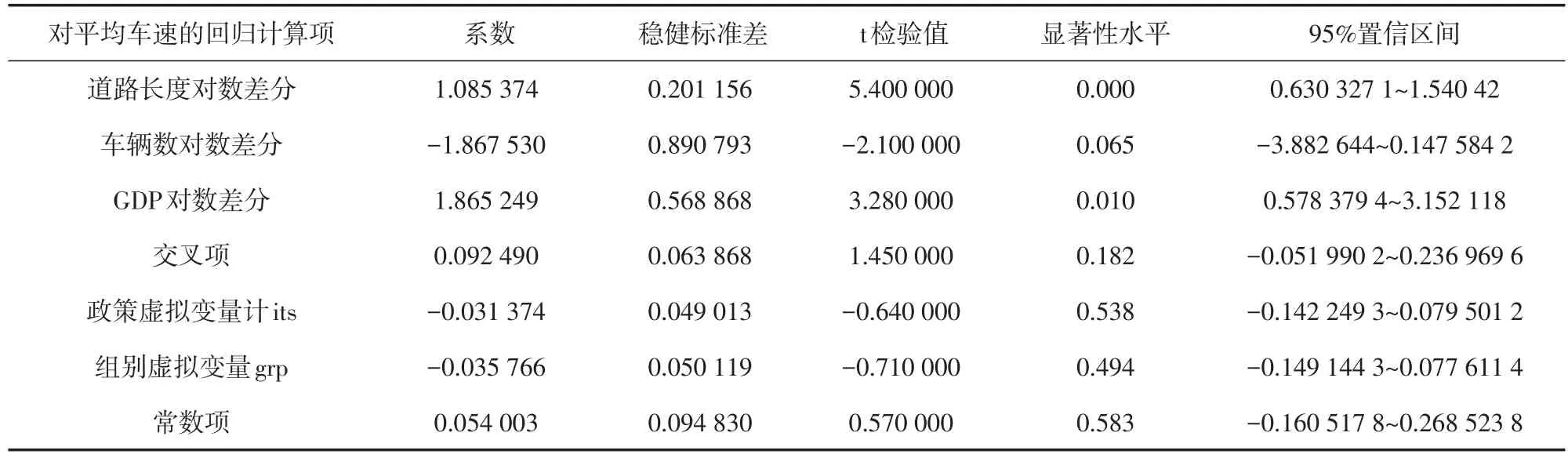
表5 模型估计结果

模型估计可决系数为0.704 1，回归的残差平方根为0.063 93，模型的解释性和稳定性均具备一定的实际价值。根据模型的估计结果，可以得出以下结论：

（1）实施智能交通项目对评价城市路网平均车速提高的净贡献为9.2%，即评价城市“畅通性”的提升，其中9.2%是由智能交通项目贡献的。

（2）从可决系数来看，包含4个变量和2个自由虚拟变量的模型解释了总变动的70.41%，其余约30%的车速提升是模型未包含的因素造成的，其中包括系统性误差、遗漏变量、变量约简误差、其他无法解释的误差等。

3 结语

笔者在传统的双重差分政策效应评估模型的基础上，引入匹配得分算法，构造适合于多因素剥离评估的基于匹配和双重差分的评估模型，并选择了36个城市，采集了基础数据，利用模型进行了定量评估。从模型估计的结果来看，交通信息化建设对城市交通运行效率提升的效果较为明显，研究中所考察的样本城市其城市交通路网车辆运行车速的提升中超过9.2%的效果是来源于城市智能交通建设项目的贡献。在“互联网+”的浪潮下，推动城市智能交通项目的建设和发展，利用信息化技术改造传统交通运输行业是交通运输业转型升级发展的必然之路。建立客观科学的交通信息化贡献评估体系有助于正确认识和客观评价交通信息化项目建设对交通运输效率提升的贡献和作用，也有助于推动行业信息化的发展。

从本项研究来看，尽管模型精度和稳健性估计都能通过，但是从实际操作来看，仍有进一步改进完善的空间。一是在自变量选择方面，受数据来源和数据延续性的影响，并不能保证将最能影响城市交通运行效率的因素准确地挑选出来作为输入变量。二是在对照组城市的选择方面，受客观条件的限制和计算简化的需要，进行了一定的主观控制，并未能完全遵从随机大样本选择的理念。三是从模型稳健性检验来看，选择不同的对照组城市，评价结果还是会存在一定的偏差，需要对模型的重点参数和估计方法做进一步的改进和完善。