基于交路单元的高速铁路乘务交路编制模型与算法

李 雯，贾富强，杨 睿，何东东

（兰州交通大学交通运输学院，甘肃 兰州 730070）

0 引言

乘务交路计划编制是高速铁路乘务部门组织、管理工作的重要环节，是运营管理的核心问题之一。在实际工作中，乘务交路计划是基于经验和乘务工作要求，由人工编制而成，存在编制方案单一、效率低下的问题，无法适应我国高速铁路快速发展、运行图变化调整的客观需要。

国内外学者针对乘务交路计划编制问题进行了大量研究。王莹等[1]通过构建时空网络模型对该问题进行描述，并设计了列生成法嵌入分支定界算法，对京津城际列车数据进行了验证计算。陈岩岩[2]将列生成算法引入该问题中，并在求解中使用了Dijkstra算法。田志强[3]将这一问题看作一类特殊的旅行商问题（Travelling Salesman Problem,TSP），并建立了基于费用最小的交路段生成模型。杨国元等[4]通过改进的Dijkstra算法求解交路与车次的匹配问题。郭璞[5]针对机车乘务排班问题，分别用模拟退火算法和拉格朗日松弛算法对该问题进行了计算。李献忠等[6]、丰富等[7]建立了广义费用排班优化模型，并将时间均衡度作为排班模型的重要组成部分。胡汪源[8]将该问题看作一个车辆路径问题（Vehicle Routing Problem,VRP），以乘务人数最少、总等待时间最少为目标构建模型，并使用遗传算法对该问题进行解决。石俊刚等[9]将任务之间的连接看作网络，并使用列生成算法对问题进行了计算。石刚[10]建立了乘务交路总接续时间最短和乘务人员的实际工作时间与工作时间标准相适应的双目标问题模型，并使用遗传算法对问题进行求解。张哲铭等[11]将该问题归类为仅考虑“相对时间”约束的组合优化问题，提出了基于时空接续网络和网络流模型的求解策略。Oketch[12]针对航空乘务排班的特殊性，通过启发式算法实现了乘务交路的自动化编制。Hoffmann等[13]针对德国铁路客运实际问题，应用混合列生成方法，通过遗传算法解决定价问题。Shen等[14]构建了基于费用最小的集合覆盖交路生成模型，并使用遗传算法使求解目标班组数目不断接近期待值。Şahin等[15]用时空网络最小流模型对该问题进行了描述，并从计算结果和计算时间两个方面比较了序贯算法和贪心算法求解该问题的优劣。

本文在已有研究的基础上，从更贴近工作实际和管理需求的角度出发，构造以交路单元为基本单位的乘务交路编制模式，在区分车体接续的基础上，以花费最小为目标，通过计算机自动生成乘务交路的优化模型及算法。

1 乘务交路编制问题分析

高速铁路乘务交路计划编制问题是指根据列车开行方案、动车组车体运用计划、乘务基地设置等相关条件对各值乘任务进行组合的计划编制过程。在编制过程中要对人员工作能力、劳动强度、出退乘地点、交接作业流程等进行统筹考虑，力求实现值乘任务全覆盖、降低成本的编制目标。

结合工作实际，本文提出交路单元的概念。交路单元是指同组列车车体及乘务人员从乘务基地车站出发行驶至折返站，并在最短时间内由折返站出发返回至乘务基地车站的过程。本文将交路单元作为编制乘务交路的基本单位，主要原因如下。

（1）客运乘务交路优化的核心问题是客运乘务人员的异车体换乘作业。客运乘务人员要对始发至终到的所有旅客及随车备品负责，这就要求异车体换乘作业只能在全程作业结束后执行，因此换乘作业只能在折返站或者乘务基地站执行。

（2）乘务基地站与折返站在功能上存在不同，除具备指挥、出退乘、学习、住宿、餐饮功能外，乘务基地还具有应对各类突发事件时启动热备车体、班组及各类应急处置的功能。

因此，通过交路单元的形式，将换乘作业执行地点设置在乘务基地站，能保证突发情况时应急处置的需要，从而最大程度地提高乘务交路计划的稳定性。值乘区间见图1，交路单元见图2。

图1 值乘区间

图2 交路单元

乘务交路计划编制流程如下：①根据列车运行图，将乘务任务分割为由乘务基地至折返站及由折返站至乘务基地的值乘区间；②由值乘区间按FIFO（先进先出）的原则组合成为交路单元；③将交路单元组合成为乘务交路。

在文献[3]的基础上，对编制乘务交路计划时需要考虑的各项费用进行如下分析。

（1）出乘、退乘费用

乘务员出乘、退乘费用主要包括乘务员班组一次值乘任务所需耗材等支出的相关费用，通常为定值Cct。出乘、退乘费用的多少取决于乘务班组数量，而乘务班组数量优化关键点在于缩短交路单元间的衔接时间。

（2）值乘费用

根据现行铁路值乘费用Czc核算标准，其主要取决于执行交路的始发时刻和终到时刻的时间差，优化关键点在于缩短交路单元间的衔接时间。

（3）换乘与便乘费用

在乘务交路j中的换乘次数aj影响乘务计划的稳定性，且会导致乘务工作质量的下降和备品的遗失，同时异车体换乘需要满足一定的接续时长。令乘务班组一次换乘的费用为chc，则交路j的换乘基本费用为ajchc。便乘涉及乘务员便乘车次和座位，涉及客票的扣除，一般不提倡出现便乘。

2 优化模型的建立

2.1 分解列车运行图

根据列车运行图，将其中的运行任务按方向摘出，并划分为A,B两个集合，分别代表离开乘务基地方向和到达乘务基地方向的值乘区间。划分后的值乘区间由下式表示：

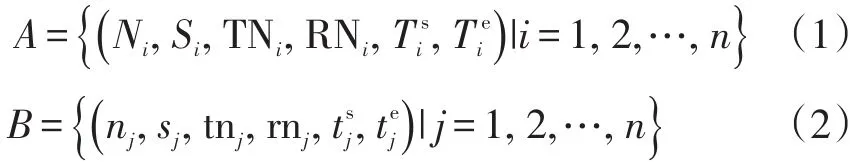
式（1）和式（2）中：Ni为离开基地方向的值乘区间序号；Si为离开基地方向值乘区间的折返站；TNi为离开基地方向值乘区间的车次；RNi为离开基地方向值乘区间的车体号；为离开基地方向值乘区间的列车基地始发时刻；为离开基地方向值乘区间的列车终到折返站时刻；nj为到达基地方向值乘区间的车次；sj为到达基地方向值乘区间的始发站；tnj为到达基地方向值乘区间的车次；rnj为到达基地方向值乘区间的车体号；tsj为到达基地方向值乘区间的列车折返站始发时刻；为到达基地方向值乘区间的列车终到时刻。

2.2 交路单元生成模型

由于乘务员班组折返时遵守列车运行图“先进先出”的原则，因而按照列车运行图将值乘区间组合成为交路单元，交路单元生成模型为：

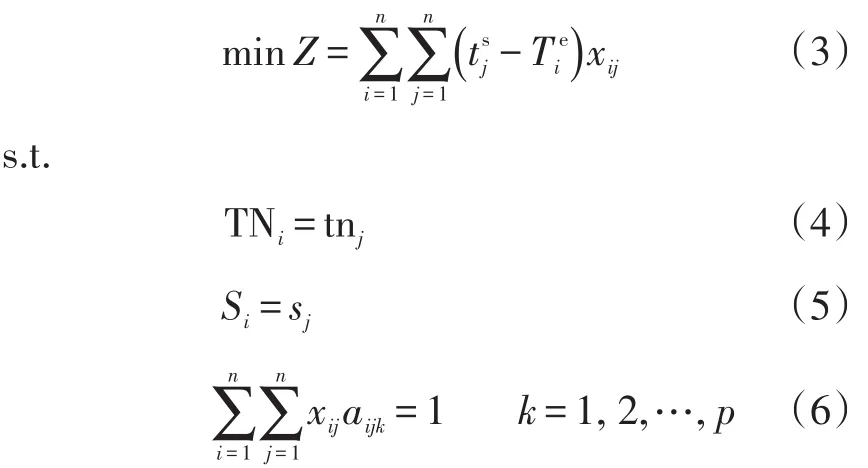
式（3）～式（6）中：xij为0-1变量，当值乘区间i和值乘区间j在同一交路单元时为1，否则为0；aijk为0-1变量，当交路单元k覆盖值乘区间i和j时为1，否则为0；目标函数（3）为最小化折返站接续时间（min），即求符合运行图“先进先出”原则列车；约束条件（4）表示值乘车体相同；约束条件（5）表示折返站相同；约束条件（6）表示值乘区间全部被覆盖且无重复选择。

交路单元的集合U，由下式表示：式（7）中：Nk为交路单元序号；TNk为交路单元覆盖车次；RNk为车体号；Tks为交路单元的基地始发时刻且=；为交路单元的基地终到时刻且=；Sk=Si=sj表示交路单元的折返站。

2.3 乘务交路优化模型

最小化费用的首要问题是减少值乘班组的数量及缩短整体值乘时长。在文献[3]的基础上，本文建立了针对客运乘务组同车体换乘和异车体换乘接续时间差异的最小费用乘务交路生成优化模型，并以交路单元为模型生成最小单位，具体如下。

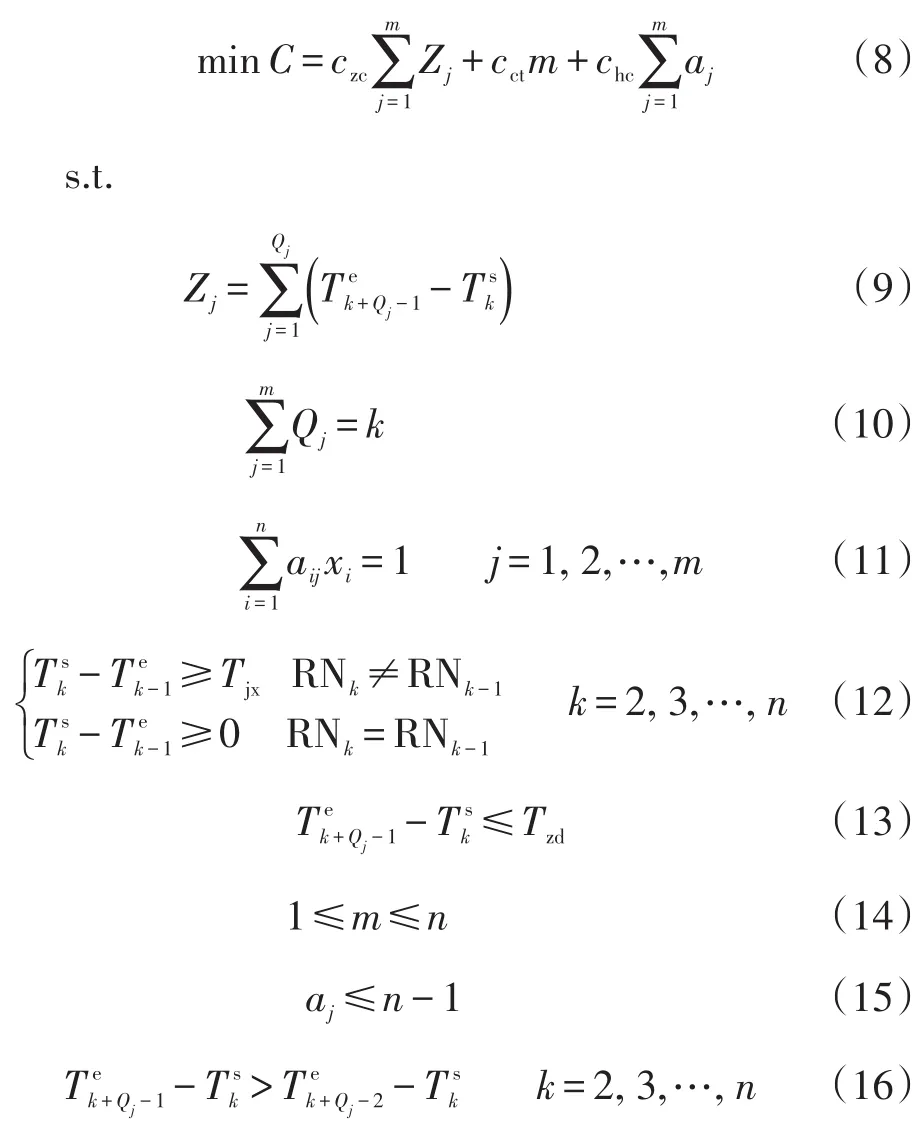
式（8）～式（16）中：m为覆盖所有交路单元的最小乘务交路数目（个），等于完成任务需要的班组数；xi为0-1变量，当交路单元i被选择进入一条乘务交路时取1，否则取0；aij为0-1变量，当交路单元j包含交路单元i时取1，否则取0；Zj为每条交路的值乘时长（min），其值为常数；Qj为每条交路所含的交路单元数（个），其值为常数，其中，i=1,2,…,n，j=1,2,…,m，w=1,2,…,Qj；Tjx为不同车体的换乘时间要满足的最小接续时间（min）；Tzd为单次交路最大时长（min）。通常，当接续时间相同时，优先选择同车体。

目标函数（8）为最小化费用；式（9）为任一交路的乘务时长；式（10）为每个交路中包含的交路单元个数k；式（11）表示每个交路单元仅能属于一个交路；式（12）表示在同车体值乘不考虑接续时间限制，而异车体换乘接续时间要大于最小接续时长；式（13）表示交路时长小于单次交路最大时长限制；式（14）表示交路数大于1、小于交路单元数；式（15）表示换乘次数小于等于交路单元数减1；式（16）表示交路中交路单元的次序。

3 模型的求解

3.1 基于贪婪思想的启发式算法设计

基于模型特点和手工编制乘务交路计划的实际，本文设计了基于贪婪思想的乘务交路生成的启发式算法。贪婪算法基本思想为：从问题的初始解出发，通过一系列的贪婪选择，逐步达到求解目标。通过每一次的迭代，要求解问题的规模都会缩小，且在每次迭代的过程中，都会保证得到最优解。通过贪婪算法求得的最优解是局部最优解，但它无需回溯和计算简单的优点对于求解乘务交路计划问题是便捷可行的。算法步骤设计如下：

（1）将列车运行图离开乘务基地方向和驶向乘务基地方向的列车分别按到达基地时刻和离开基地时刻进行排序。

（2）按照相同车体搜索并按照时间差最小组合，生成交路单元集合U。

（3）从U中选出发车时间最早的交路单元。

（4）选出发车时间与其最为接近的下一个交路单元，即满足接续时间最小。由于同车体不需要换乘和交接，故先在车体一致的交路单元中搜索，找到终到时间与发车时间差最小的交路单元。

（5）再在车体不同的交路单元中搜索，由于换车体值乘涉及换乘和交接作业，故需要在满足接续时间标准的前提下找到接续时间最小的交路单元。

（6）比较步骤（2）和步骤（3）中接续时间的长短，选择接续时间最短的交路单元与之相连接，当接续时间相等时，优先选择同车体交路单元。

（7）重复以上步骤，直到交路终到时间和始发时间之差大于单次最佳值乘时长Tzj时，停止形成一个交路，其中，Jw为交路编号；为交路始发时刻；tdw为交路终到时刻。

3.2 乘务交路优化调整

生成结果中会存在一些由值乘时长极短的单元构成的乘务交路。参照人工编制流程，以最大允许单次值乘时长Tzd为限制，对已生成的值乘时长过短的小交路进行人工调整。由于乘务班组数量与交路数量直接相关，优化调整交路的目的在于在时间允许范围内生成的交路数量最少，即保证了值乘班组数量最少。

4 算例分析

将京津城际数据作为算例进行分析。采用Java语言对所设计的启发式算法进行了实现。将京津城际时刻表录入，所生成的乘务交路单元数据如表1所示。乘务交路生成参数设置如下：Tzj=480min,Tzd=600min,Tjx=15min,Tzd=600min。对乘务交路计划进行人工优化调整后，结果如表2所示，交路时长分布效果见图3。

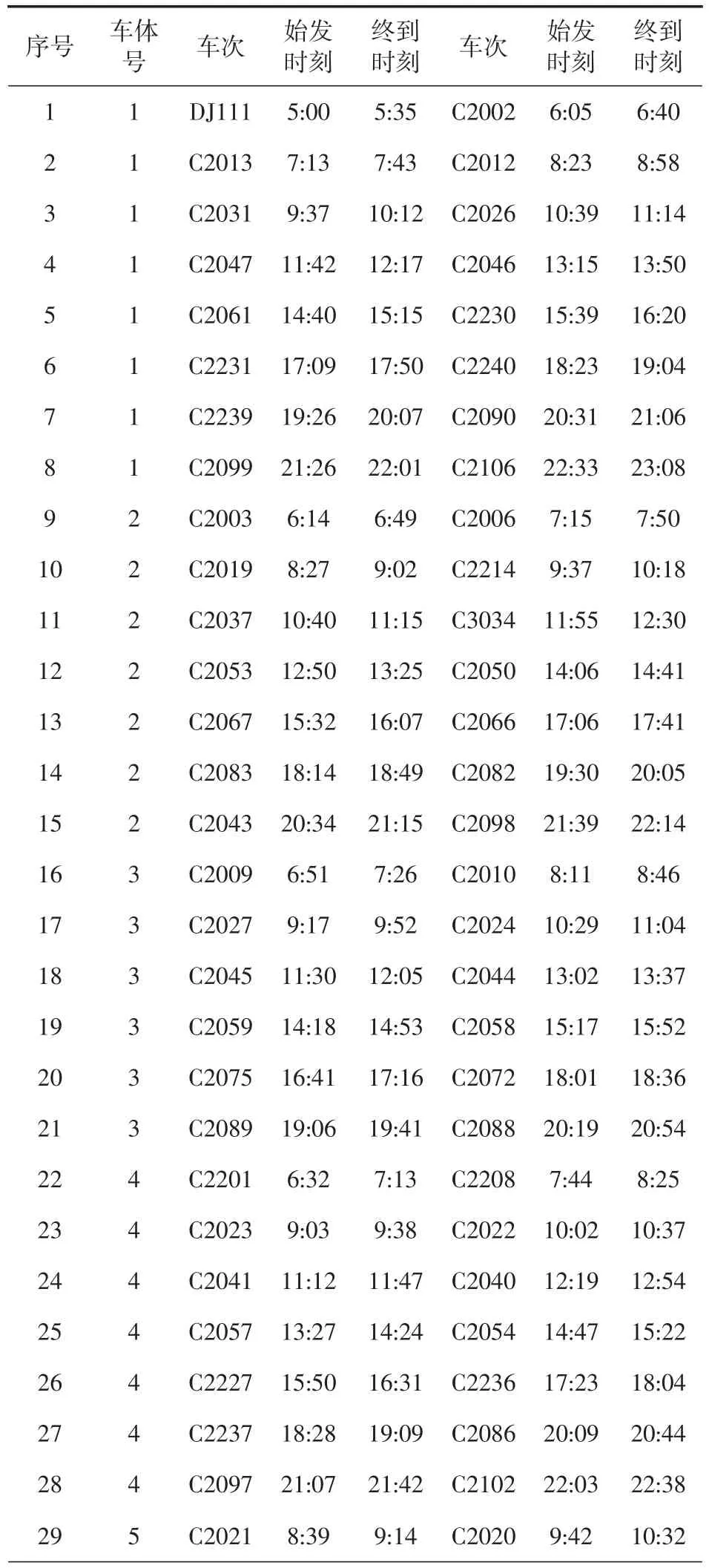
表1 乘务交路单元生成结果

表1（续）

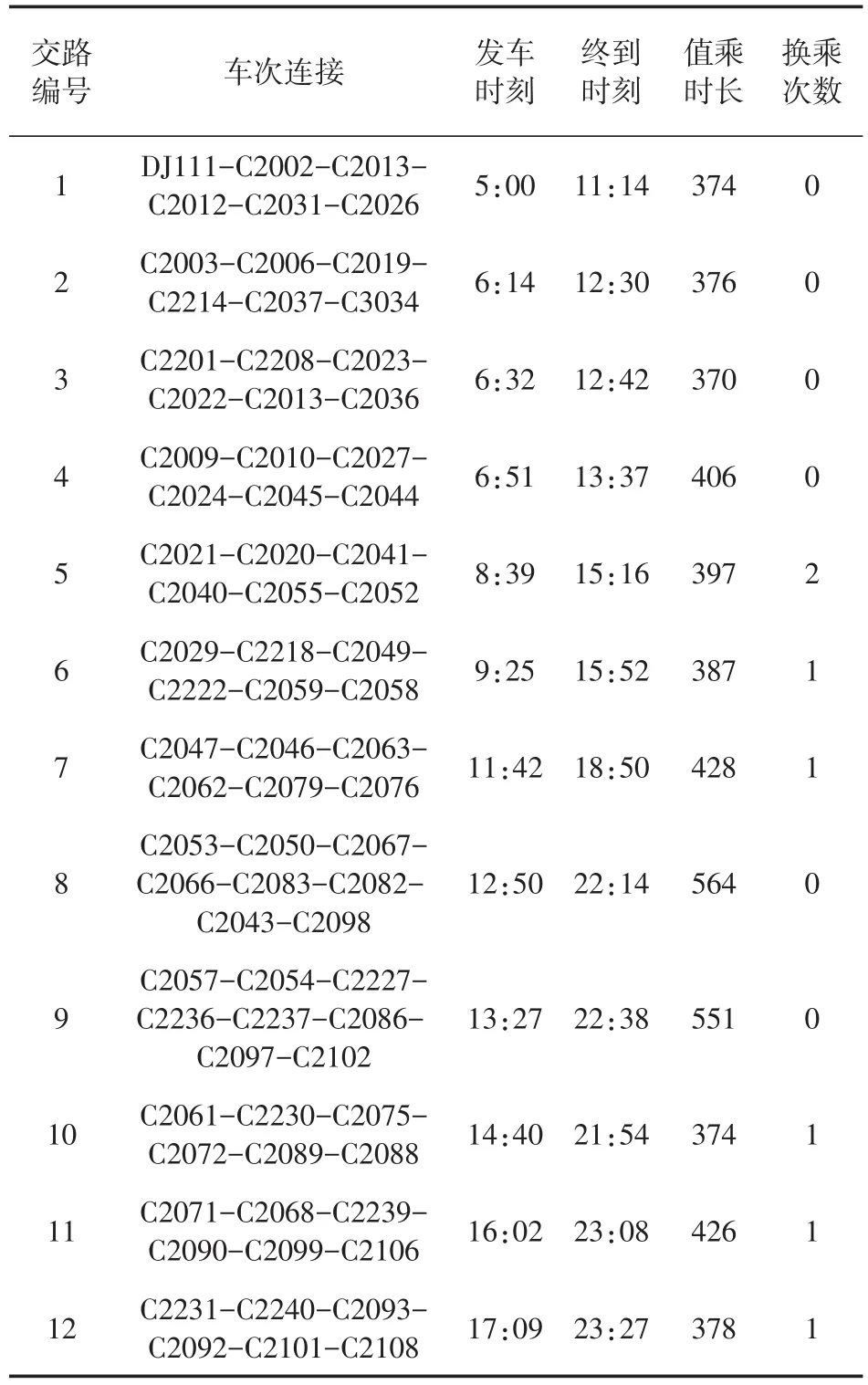
表2 乘务交路优化调整结果

从表2可知，所有乘务交路按照发车时间先后顺序排列，换乘次数在0～2之间，值乘时间在8h之内，经调整后不超过10h。由图3可直观看出各交路排布均匀整齐、便于管理，且每个交路值乘时长分布较为均衡。

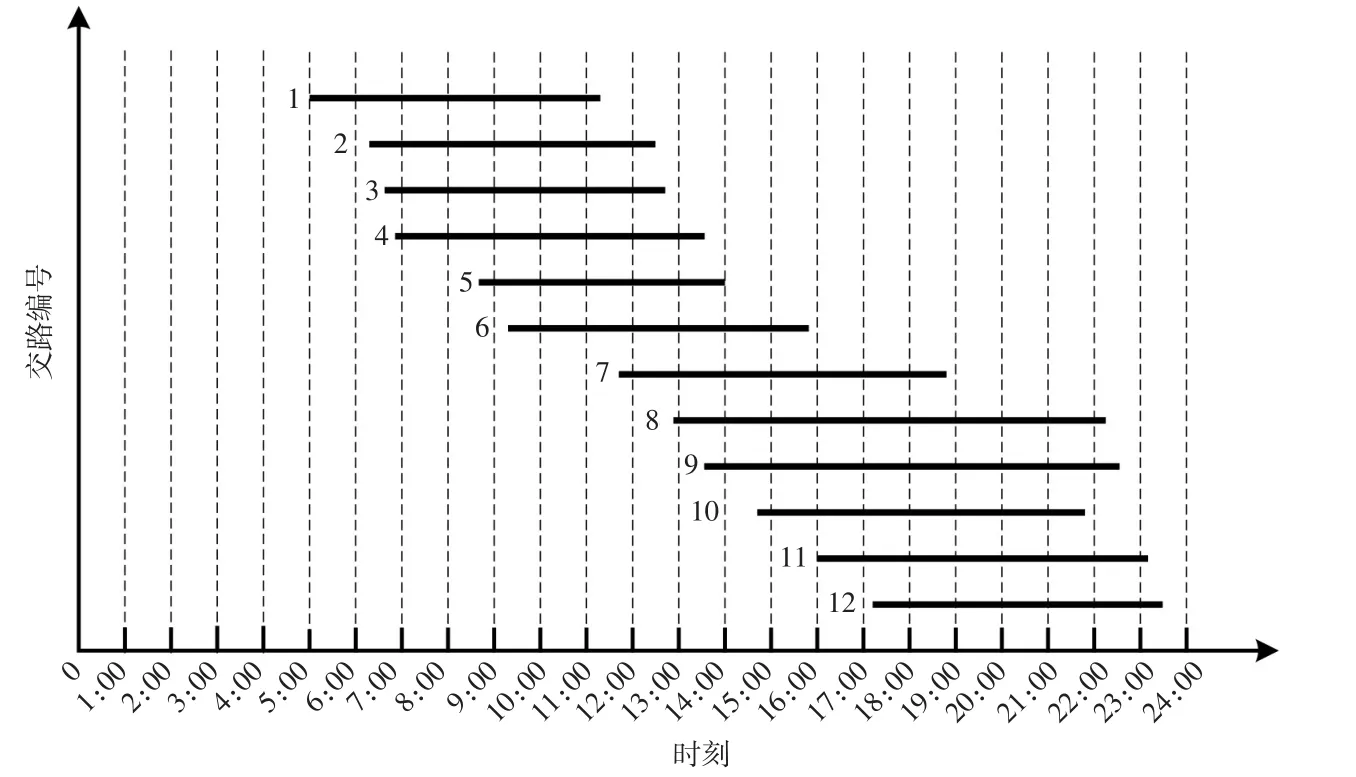
图3 交路时长分布图

5 结论

实例研究表明，本文以交路单元作为基本单位的优化模型在缩小了该问题计算量的同时满足了实际工作中出现突发情况时应急处置的需要，且能从乘务作业稳定性、可行性及管理便捷性方面满足编制要求。基于贪婪思想的乘务交路生成算法能够在短时间内自动化生成客运乘务交路计划，但在求解质量方面仍然存在改进空间，将进一步开展后续研究。