混合遗传算法的多式联运运输管理研究∗

陈利民

（北京师范大学珠海分校 珠海 519087）

1 引言

多式联运是物流系统中的主流方式，涉及运输中的路线优化选择，以运输费用或时间来衡量路线或者方式的优劣［1～2］，它可以有效地提高运输业的服务性、竞争力和综合效益，因此它拥有很强的实际意义。运输物流不仅要考虑交通、气候等多个因素，而且在实际路线优化问题中，最终确定方案的决策信息是不固定的［3］。多式联运的出现很快利用在原料的采集、物品的生产、货物的供应等重要环节。同时，在经济一体化中，多式联运的技术和理念也渴望由第三方物流发展到第四方物流［4］。

文献［5］利用层次分析以及决策论的规律，对多式联运的运输问题问题做了研究；文献［6］结合运输过程的分层系统以及多式联运网络的建构原理方法，提出了多式联运决策框架；文献［7］也提出了最优运输路径的最短路法；文献［8］将多个运输方式的联合解决运输问题，将时间条件，能力限制等作为约束提出最优路径的启发式算法。

本文主要利用混合遗传算法，通过设置约束条件，建立多式联运数学模型，对每个节点进行染色体编码，从而求解出该算法得到的最优解，仿真实验得出该算法有很强的实际利用价值。

2 多式联运的数学模型

2.1 构建模型

我们假设有一个多式联运运输方式优化问题，可以描述为，一物流公司欲将一批物资从始发地O送达目的地P，需要经过n个城市，其中任意两个相邻城市间都有K种运输方式（包括水路、公路、铁路）可以选择，显然不同运输方式的运输时间和运输成本是不同的，并且如果从一种运输方式换成另外一种运输方式，需要中转费用和中转时间。假设运输方式的中转只发生于城市内，并且不同城市的中转费用和中转时间是不一样的，那么该怎样选择运输方式，才能实现运输成本最少，运输时间最短。

假设该优化问题需满足以下四个条件［9～10］：

条件1为物资的转运只发生在城市节点，并且每个城市节点最多发生一次转运；条件2为物资在城市节点间只可以整体运载，不可以分割；条件3为物资在两个城市节点间只可以选择一种运输方式和一条运输路径；条件4为物资在每个城市节点即时中转，没有库存。

在上述的多式联运运输方式优化问题中，需要同时考虑最小化运输总成本和运输总时间，这两个目标的数学模型可以描述为

目标函数：

约束条件为

2.2 运输方式与运输路线优化的关系

多式联运中每两个节点之间的运输方式以及运输路径是有密切联系的［11］。若选择某种运输方式如图1（a），不同的线表示不同的运输方式，图1（b）表示该运输方式所对应的运输路径。在某种运输方式下选择的路线是判断运输方式好坏的依据。

3 混合遗传算法

3.1 算法原理

通过对上述问题以及模拟运输网络图的分析能够发现，该运输方式优化问题实质是约束条件下的最短路问题［12～13］。即在给定的约束条件下，实现目标城市对间路线的最优组合问题。因此，本文试图采用随机化搜索，即遗传算法来实现各城市对间路线的最优组合。第一步先进行编码和群体初始化（群体数量为K）生成一组方案集，分别算出各个方案的运输总成本 Fˉ(k)    (k=1，2，…，K)；第二步对Fˉ(k)进行排序，可以采用区间数排序来辨别个体的优劣，以此为依据构造混合遗传算法寻求最优路线组合方案。随机化搜索路径如图2所示。

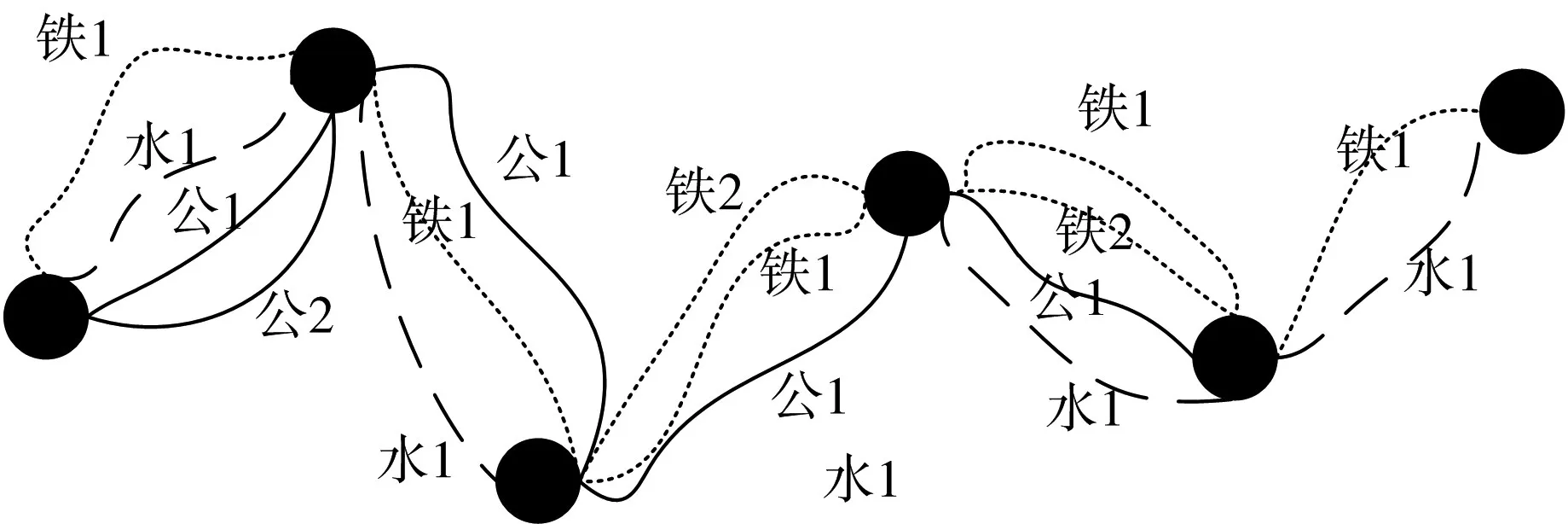
图2 随机化搜索路径图

3.2 染色体编码技术

模型中我们采用字符代码对其进行编码，其中城市对间的运输路线编号代表该问题的染色体编码［14］。如果从运输始发地O到目的地P之间需要经过n个城市，从始发地O到目的地P之间要经过2n+1个虚拟城市。我们用一组2n+1个数字来代表一个运输路线组合的染色体编码。

例如：

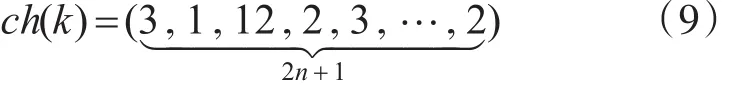
即在始发地和城市1组成的城市对间我们选取第3条路线，在城市1和城市2组成的城市对间我们选取第1条路线……在城市n与目的地组成的城市对间我们选取第2条路线。最初群体初始化时，每个染色体的第 1，3，5，7，…，2n-1，2n+1个基因是从城市对间的路线编号中随机生成排列得来，第 2，4，6，…，2n 个基因分别与第 3，5，7，…，2n+1个基因相同，故可以直接复制。根据某个染色体的编码串，可以记录下对应运输任务在城市对间所选取的路线。

3.3 适应度函数

假 设 存 在 某 一 染 色 体 为 ch(k)=(y1，y2，…，y2j-1，y2j，y2j+1，…，y2n，y2n+1) ，它 的 意 思 是 在 城 市j-1与城市 j组成的城市对间选取第 y2j-1条路线，在城市 j与城市 j+1组成的城市对间选取第y2j条路线。到达城市 j时，需要从第 y2j-1条路线转换成第 y2j条路线。我们将运输总成本Fˉ(k)视作染色体ch(k)所表示的路线组合方案的目标函数［15］：

运输总时间方程：

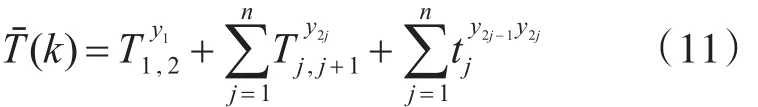
构造的适应度函数Eˉ(k)如下：

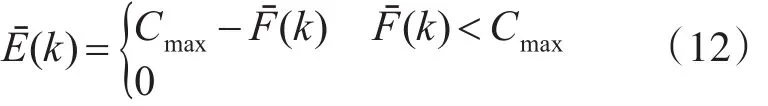
其中Cmax是一个恰当的输入值。个体的适应度与其适应度函数值成正相关，并且个体遗传到下一代的概率与适应度也成正相关。

3.4 构造遗传算子

首先：选择算子，第一步对群体中的所有个体进行排列，依据适应度值从大到小的次序进行，之后将其均分为10组；第二步依次将第l组中所有个体复制两份，将第2～9组中所有个体复制一份，第10组不复制。这样选择算子可以保证每次进化都可以使适应度高的个体被复制到新的种群中，同时群体规模不变。

其次：交叉算子，即群体间随机配对，从而将随机生成交叉点位置，再单独用交叉概率交换交叉点后的基因，生成新的个体。为确保新个体为有效染色体，我们对交叉点位置做如下设计：设ch(x)、ch(y)为一对交叉染色体，交叉点是第k个基因座之后，那么k取值为

其中 rα为[0 ， 1]内一个服从均匀分布的随机数；n表示经过的城市数量；round()表示四舍五入到最接近的整数。

最后：变异算子，ch(x)=(c1，c2，…，ck，…，c2n+1)向 ch*(x)=(c1，c2，…，，…，c2n+1)。

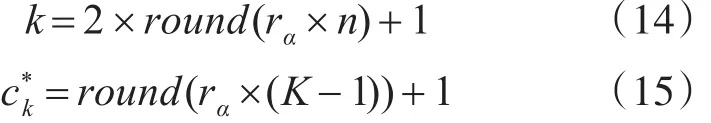
其中 rα为[0 ， 1]内一个服从均匀分布的随机数；n表示经过的城市数量；round()表示四舍五入到最接近的整数。K是城市对间路线数量。对个体ch(x)=(c1，c2，…，ck，…，c2n+1)进行变异的具体操作设计如下：

2）若 k=1，则令 ck=；若 k≠1，则令 ck=且ck-1=，随即产生新的个体。

3.5 算法流程

结合上述分析，混合遗传算法的多式联运运输路线优化问题的步骤如下：

Step 1：群体初始化 G(s)，s=0（s是进化的代数，G(s)是第s代群体），设群体数量为M，对初始化群体进行编码。

Step 2：计算个体的适应度Eˉ(k)及其对应方案的运输总时间 Tˉ(k)。

Step 3：若 Tˉ(k)＞ Tˉ0，则删除该个体。

Step 4：若在步骤3中删除了q个个体，为保证群体内个体数量不变，则从剩余群体中复制q个个体。

Step 5：对群体中的所有个体按照适应度从大到小的顺序进行排列。

Step 6：若 s≤S（S是遗传运算停止条件），那么转到步骤7，反之转到步骤1。

Step 7：对群体G(s)进行选择操作。

Step 8：用交叉算子对群体G(s)实行交叉操作。

Step 9：用变异算子对群体G(s)实行变异操作。

Step 10：对群体的多样性进行判断和调整。

Step 11：得 到 新 一 代 群 体 G(s+1)，G(s)←G(s+1)，s← s+1，转步骤2。

Step 12：对适应度最大的染色体解码，从而结束遗传迭代。

4 仿真实验

仿真中假设一批货物，重量是4000t，时间要求在［40h～50h］从O地运送到Q地。O、Q两处之间的运输网络信息（表1）以及换装信息（表2），另外货物的特殊性，使得增加了其他约束条件中途换装次数不能多于两次，通过混合遗传算法求解最佳运输路径，最佳运输方式求解最佳的运输方式，使得组合使总费用最省，并且时间期限也到达到客户标准。

表1中给出了每条线路中每个节点的运输费用范围以及运输时间范围，表2给出每个节点的换装时间与费用，这都是算法中的约束条件，用来求解最优解。

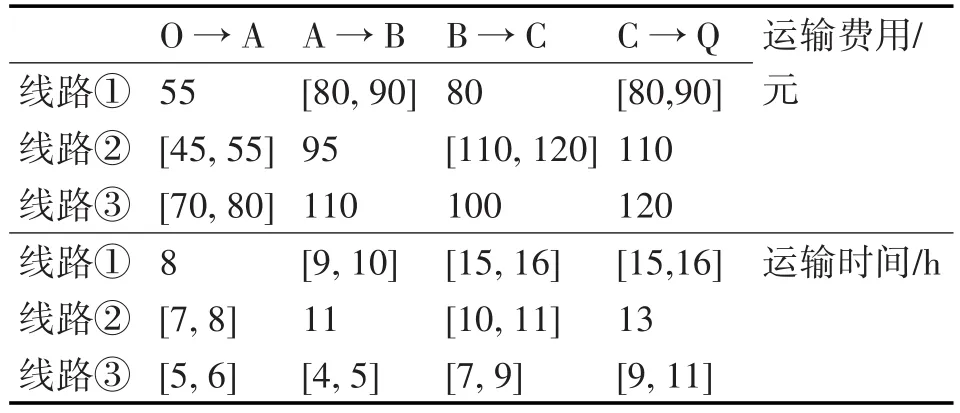
表1 运输网络信息

表2 换装信息

取群体规模M=50，交叉概率是0.7，变异概率为0.01，迭代次数为50，用本文的混合遗传算法程序对该问题进行最优化求解。如图3可知，当迭代到第5次时，优化结果不变，此时运输总费用是［350，370］范围，而运输的总时间范围是［35，42］，运输总费用和运输总时间随进化代数的变化曲线如图3所示。算法求解的最优结果为运输路线方式是5即②→②→②→③，运输的虚拟运输网络如图4。

图3 运输总费用与运输总时间变化图

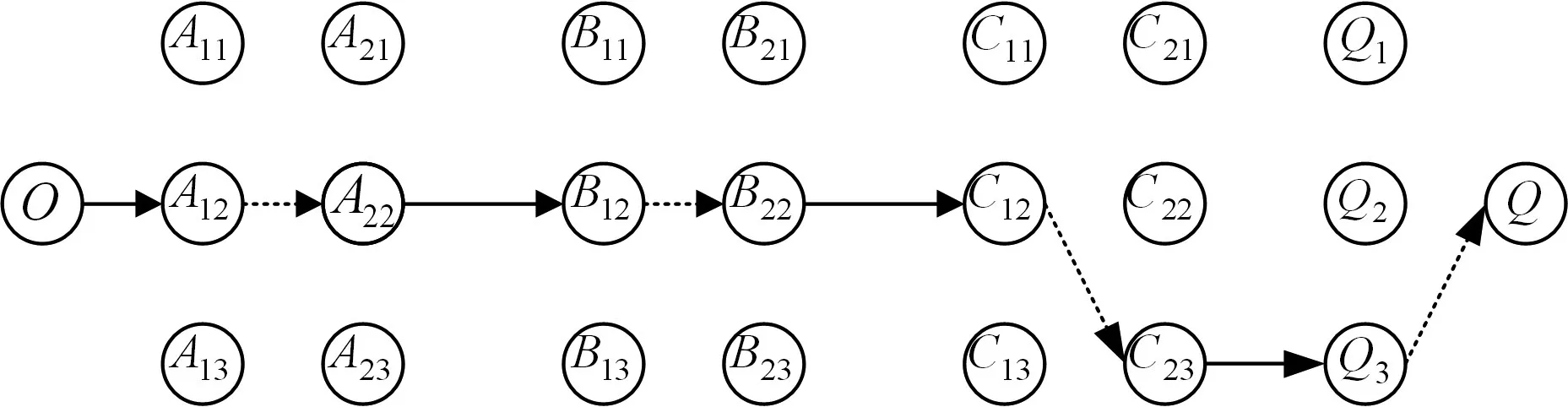
图4 求解结果虚拟运输网络图

5 结语

本文对于多式联运问题中运输路径以及运输方式的多样性的客观需求和目标客户对货物运输时的经费、时间等实际的要求作为约束条件，基于以上问题本文提出了运输方式和运输路径构成优化模型，设计混合遗传算法对优化模型进行求解，通过实际的运输路径、运输费用、运输时间以及换装次数等多个要求进行算法迭代，获得优化的运输方案，通过实例对模型及算法进行检验，可以很好地供应商提供更好的选择方案。