狼群算法优化自抗扰控制器的应用∗

刘晓丽 兰 英

（1.武昌工学院 武汉 430065）（2.成都理工大学工程技术学院 乐山 614000）

1 引言

自抗扰控制器（Active Disturbance Rejection Controller，ADRC）是由中科院韩京清等经过近三十年的深入研究而提出的新型非线性控制器，具有超调小、响应快等优点，已经在许多领域得到广泛应用［1～3］。

将自抗扰控制器用于机器人手眼协调控制系统对提高机器人的控制性能具有重要意义。该控制方式的前期目标是针对一些特定的应用任务，如机器人手爪定位于静止目标或跟踪运动目标等，之后可将该技术推广成为机器人视觉伺服系统的一般理论。大量研究已对基于ADRC的机器人无标定手眼协调控制系统的设计进行了详细的讨论，证明ADRC具有解决此类问题的良好性能和巨大潜力［4］。

而自抗扰控制器中众多参数的整定理论及方法一直是ADRC研究中的重要组成部分，也是使该控制器得到更加广泛应用的重要前提。现代参数优化算法［5～7］的成果已在很大程度上丰富了ADRC的理论研究［8～10］，同时也为 ADRC应用于机器人无标定手眼协调控制提供了重要的理论依据。

人工狼群算法的产生起源于自然界狼群在捕食和猎物分配中表现出来的群体智能［11～12］，已成功应用于解决带有连续变量的全局优化问题。文献［13］对狼群算法中的围攻策略进行了改进，模拟计算了奔袭步长并提供了有效取值范围，实例表明，狼群算法能有效应用在水电站水库优化调度问题的求解上。文献［14］仿真结果表明用狼群算法进行全局最大功率点跟踪的效果较好，文献［15］将狼群算法应用于无人机航迹规划，取得了满意的结果。

本文提出采用狼群算法解决自抗扰控制器参数优化问题，并应用到机器人手眼协调控制系统中，大量的仿真实验验证了算法的有效性。

2 狼群算法

狼群是以头狼为中心的，整个猎捕活动可以分为5个重要部分，即狼群初始化、竞选头狼、靠近头狼、狼群围猎以及狼群更新。

1）狼群初始化

此阶段的关键是让狼群均匀分布在目标函数的定义域内。设定狼群规模为N，搜索空间的维数为D，第i匹狼的位置为

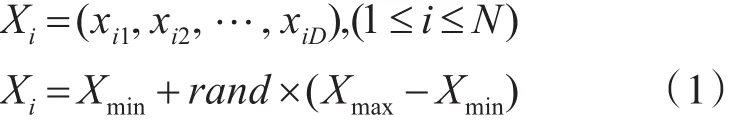
其中，rand是在［0，1］区间内均匀分布的一个随机数，Xmax和Xmin分别是搜索空间的上下限。

2）竞选头狼

为了选出狼群中最强的头狼，先取目标函数值最好的n匹狼作为竞选狼，它们在自己周围的s个方向进行搜索。

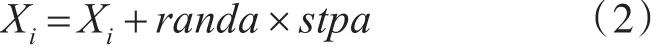
其中，randa是在区间［-1，1］内均匀分布的一个随机数，stepa是搜索步长。

如果新产生的位置优于当前位置，则用其替换当前位置，然后继续进行搜索。当搜索次数大于最大搜索次数hmax或者搜索到的位置不如当前位置，则结束搜索。最后选出占有最优位置的狼作为头狼。

3）靠近头狼

其它的狼向着头狼的位置移动：

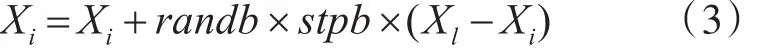
其中randb是在区间［-1，1］内均匀分布的一个随机数，stepb是移动步长，Xl是头狼的位置。

更新后的位置若优于当前位置，则将其作为当前的位置，反之则狼不移动。

4）狼群围猎

生成一个在［0，1］内的随机数rm，预先设定的一个阈值rth。如果rm比rth小，则狼不移动；如果rm比rth大，则狼群以头狼为中心对猎物进行包围。更新后狼的位置为

其中stpc为包围步长，它会随着迭代次数的增大而减小，产生方式如下：

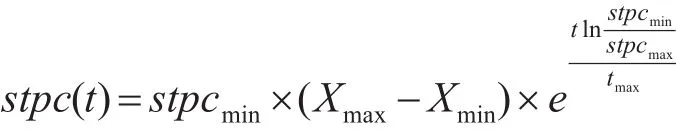
其中，t为当前迭代次数，tmax为最大迭代次数，stpcmax最大包围步长，stpcmin为最小包围步长。

5）狼群更新

根据优胜劣汰的原则，去掉最差的m匹狼，再按式（1）随机生成m匹狼，使种群不易陷入局部最优且具有多样性。

3 仿真研究

被控对象是MOTOMAN-SV3机器人，它有6个旋转关节，采用D-H方法描述各连杆坐标系，根据连杆参数可得到机器人的正向运动学方程和相应的雅可比矩阵。

三维世界坐标系中的点W(xw，yw，zw)（单位：mm）到图像坐标 P(px，py)（单位：pixel）的变换关系为

其中，fx=f Nx，fy=f Ny，有效焦距 f=6mm ，是图像平面到投影中心的距离；x，y方向的比例系数Nx=0.0082，Ny=0.0072，是CCD阵列上 x，y方向两相邻像素点间的距离；=[1 0 0]T，=[0 1 0]T，=[0 0 1]T；CCD阵列的中心在图像中的位置 Xc=165，Yc=140。平移矢量T=[40，10，1500]T，旋转矩阵其中倾侧角 ψ=80°、俯仰角 θ=-70°、旋转角φ=-160°。

仿真实验中所用的一阶离散自抗扰控制器方程为

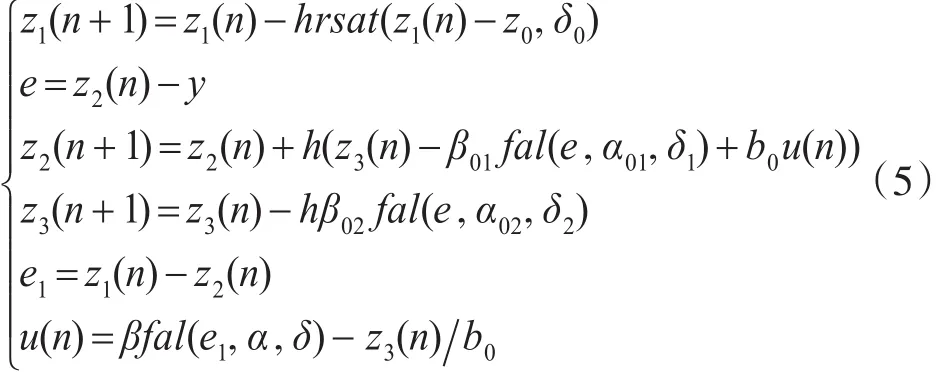
z0，y分别是给定输入和实际输出，h是仿真步长，取值0.1。

最优指标的选取考虑了系统的综合性能及控制能量问题，其形式为

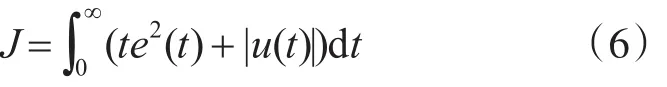
狼群算法优化式（5）中的 r，β01，β02和 β ，具体实现步骤可描述如下：

Step 1：参数初始化，包括狼群中狼的个数N=50，搜索空间的维数D=8，最大迭代次数tmax=200，竞选头狼的个数n=10，搜索方向s=4，最大搜索次数hmax=5，搜索步长stepa=1.5，移动步长stepb=0.9，最大包围步长stpcmax=0.9，最小包围步长stpcmin=0.2，最差狼的个数m=5，按式（1）对每匹狼的位置进行初始化；

Step 2：将当前位置数据代入控制器中，并将控制作用施加到被控对象上，按式（6）计算目标函数值，选择目标函数值最优的n个位置的狼来竞选头狼，竞选狼通过式（2）不断搜索到更优的位置，最后选取当前最优的竞选狼作为头狼；

Step 3：其他的狼按式（3）进行位置更新，向头狼位置移动；

Step 4：狼群通过式（4）对猎物进行围攻；

Step 5：去掉目前最差的m匹狼，然后按式（1）随机新生成m匹狼；

Step 6：判断是否满足结束条件，若满足则退出循环，记录当前头狼的位置；否则，跳转到Step 2。

最终优化得到的控制器参数为

水平方向：

r=15.26，β=33.42，β01=1.45，β02=0.37

垂直方向：

r=10.37，β=76.74，β01=2.43，β02=0.96

当目标作圆周运动时（单位：pixel）：

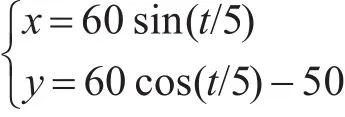
仿真结果如图1～图3所示。

图1 手爪运动轨迹与目标运动轨迹

图3 垂直方向的控制量和误差

由图可知，机器人手爪能及时跟踪上运动目标，稳定后两个方向的误差均不超过1个像素。

用同样的控制器参数，让目标沿椭圆形运动时（单位：pixel）：

仿真结果如图4～图6所示。

由图可知，手爪依然能以较高的精度跟踪上运动目标，说明狼群算法优化后的控制器参数有较强的适应性。

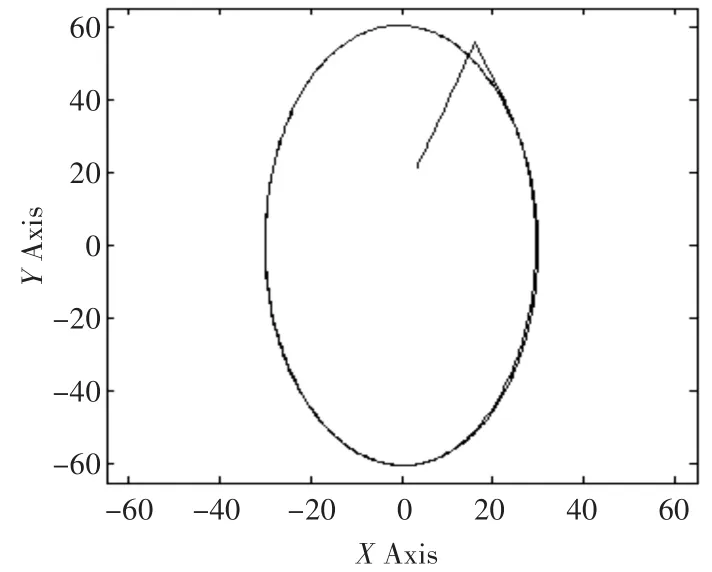
图4 手爪运动轨迹与目标运动轨迹

图5 水平方向的误差量

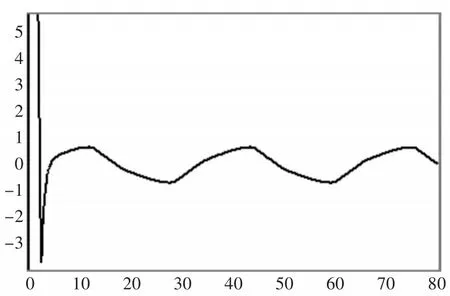
图6 垂直方向的误差量

4 结语

目前，对自抗扰控制器的研究仍处于不断拓宽与深入的阶段，关于机器人无标定手眼协调这一典型任务的考察及性能拓展既是进一步开阔ADRC应用领域的重要途径，也是丰富ADRC理论的重要手段。本文采用狼群算法优化自抗扰控制器的参数，是符合当前研究趋势的一个新方向。