基于ARMA模型的黄金价格短期预测分析

费一凡 陶雨芊

（北京工商大学经济学院，北京 100048）

黄金是一种具有货币和商品双重属性的特殊贵金属，因其卓越的避险功能和对抗通货膨胀的能力，一直是投资的热点。其价格变化也直接决定了黄金投资者和生产者的价值行为，因此黄金价格的变化备受关注。一方面，对黄金价格进行准确的预测，有助于投资者了解黄金市场的特征，预测黄金未来的行情，为他们进行决策提供帮助，从而更理性地在黄金市场中进行投资；另一方面，根据黄金价格的变动制定适当的投资策略，对于帮助投资者把握投资机会，根据自身的资金规模和财富基础选择投资品种和投资时机具有重要意义。所以，判断和预测黄金价格成为了学者研究的一个重要课题。

一、研究现状

国内外学者较多的关注影响黄金价格变动的因素，研究影响因素的变动如何影响黄金价格。其中，李京(2010)运用GA—BP算法分析了黄金价格，该算法忽略了黄金价格的随机波动，会带来一定的偏差。BernaUzun(2017)应用马尔可夫链模型(MCFS)研究和预测黄金价格走势的方向。刘二菊 (2014)则是先将灰色预测模型GM(1,1)与马尔科夫链结合得到灰色马尔科夫预测模型(GM-Markov模型)，随后在此基础上对模型进行改进，得到将新陈代谢灰色预测模型与加权马尔科夫链预测结合形成的组合预测模型，对随机波动性较大的黄金价格时间序列数据进行预测。由于黄金价格的特征，也有一部分学者选择运用时间序列的方法来分析黄金价格的变动。曹晶(2010)、潘贵豪(2010)分别使用ARIMA-GARCH模型对黄金价格进行实证分析，不仅并未给出预测结果，也未对未来黄金走势进行分析。徐庆娟(2017)同样使用ARIMA-GARCH模型对黄金现货收盘价格进行实证分析，不同的是分析了对黄金现货日收益率序列在未来100天内走势区间与条件标准差变化趋势，并对预测结果进行了验证。

本文将以2014年1月1日至2018年4月20日的黄金的周平均价格为例，利用时间序列相关理论建立黄金价格差分后的ARMA模型，并对黄金价格进行实证分析和预测。

二、黄金价格的ARMA模型建立与分析

（一）数据选取

本文选取世界黄金协会所公布的信息作为黄金价格水平的代表，选取2014年1月1日至2018年4月20日的黄金历史价格。为了使本文的研究数据不受特殊值影响，我们在公布的原始数据序列的基础上，根据一周5个交易日来计算出黄金的周平均价格，得到数据224个。其中黄金价格以克为单位，人民币计价。

（二）模型的预处理

本文使用Eviews6.0进行数据分析。首先得到样本2014年1月1日至2018年4月20日的黄金的周平均价格X的时序图，如图2.1所示，在2016年以前黄金的价格呈下跌趋势，2016年出现大幅上涨，随后依旧呈下跌趋势。因此我们判断X应该是非平稳的时间序列。

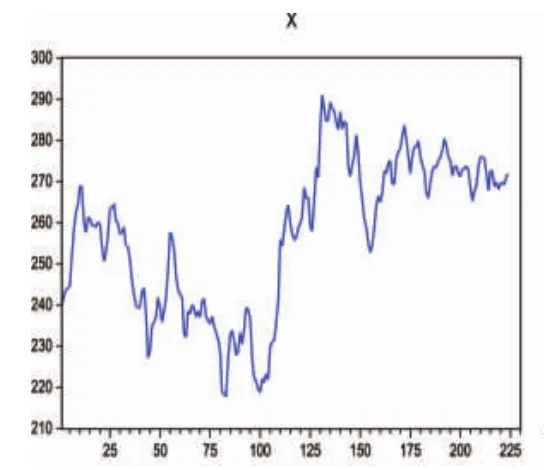
图2.1 黄金的周平均价格时序图

图2.2 黄金的周平均价格一阶差分时序图

为了进一步证明时间序列X是非平稳的，对该时间序列进行自相关系数及纯随机性检验，原始样本的Q统计量检验伴随概率见表2.1。且通过ADF检验，发现原始序列X明显的不符合平稳时间序列特征。由此可以判断黄金的周平均价格序列是一个非随机非平稳时间序列，因此我们需要对序列X进行差分处理，得到序列DX，重复上述检验。

表2.1 时间序列的纯随机性及平稳性检验（P值）

由图2.2，我们可以看到，通过作2014年1月1日至2018年4月20日黄金的周平均价格一阶差分序列DX时序图，发现原始序列进行一阶差分后，数据的趋势性基本消除了，数据大致围绕一个固定值上下波动，初步判断该序列为平稳序列。

对一阶差分后序列DX进行纯随机性检验，样本的Q统计量的P值检验显著，所以拒绝序列纯随机的原假设。同时在ADF检验过程中，依次删去斜率项和截距项，最终在无斜率及截距项情况下，单位根统计量-11.05901，小于临界值，拒绝原假设，认为一阶差分后的序列不存在单位根，序列DX是平稳的。因此可以建立ARMA(p,q)模型。

（三）ARMA模型的建立及检验

1.模型的识别。ARMA模型即自回归移动平均模型是一类常用的随机时间序列分析模型，由博克斯(Box)和詹金斯(Jenkins)创立，也称B-J方法。我们进行多次尝试，分别建立AR(1)、AR(2)、AR(3)、MA(1)、MA(2)、ARMA(1,1)、ARMA(1,2)模型，其中部分估计结果分别如下所示：

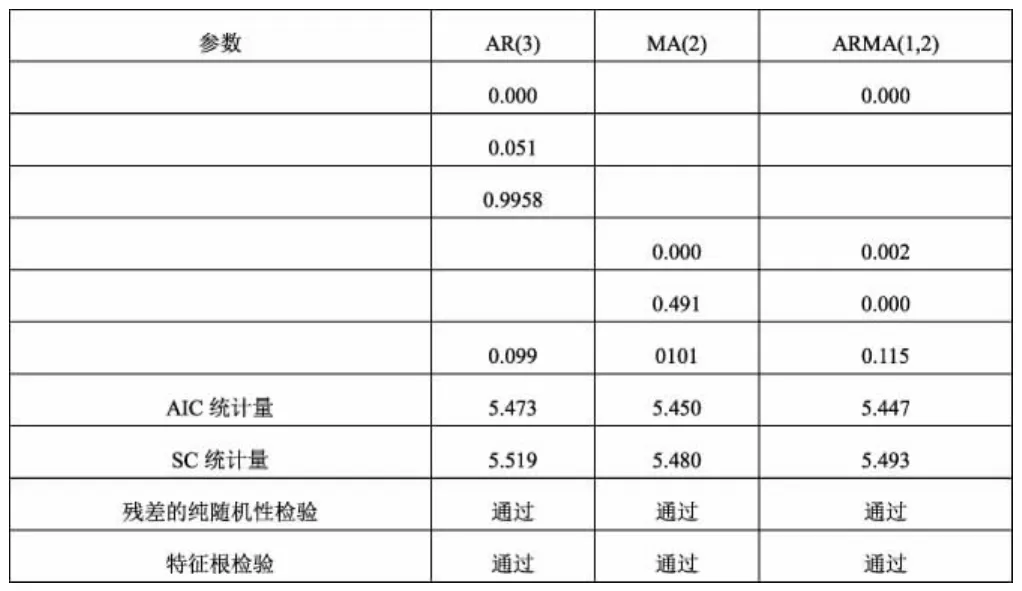
表2.2 对一阶差分后序列的回归结果分析

通过对上述所有模型的各项检验指标进行综合比较，ARMA(1,2)模型的各项参数t检验结果显著，同时拟合优度最高。且AIC、SC值相对较小。因此，综合上述各项检验指标考虑，选择ARMA(1,2)模型对黄金的周平均价格的一阶差分序列进行建模较为合适。函数表达式为：

2.模型残差的纯随机性检验。本文接下来对最终ARMA(1,2)模型的残差序列进行纯随机性检验，结果如表2.2所示。分析看出，Q统计量的相伴概率P都远大于5%的显著性水平，因此可以认为该ARMA(1,2)模型的残差项之间不具有相关关系，即残差序列是纯随机的，模型信息提取比较充分。

残差序列并不存在相关关系，且模型的效果比较好，所以判定该ARMA(1,2)模型可以进行之后的预测分析。

（四）模型的拟合及预测分析

由于ARMA模型只能依据黄金价格本身的时间序列数据进行预测，随着时间发展，其预测的精度会受到其他因素的影响而下降，随之产生误差会逐渐积累，因而只能通过该ARMA(1,2)模型进行短期预测。

表2.3 黄金价格预测值与实际值对比

表2.3是利用该ARMA(1,2)模型对2018年4月第四周到2018年6月第一周共6周的黄金价格进行的预测，预测值与实际值之间的绝对误差都较小，且预测相对差异的绝对值小于1%，与黄金当时实际均价极为接近，预测较为准确；表2.4中的预测值反映了黄金价格存在小幅度上涨的趋势，该模型在黄金价格的短期预测上具有一定的应用价值。

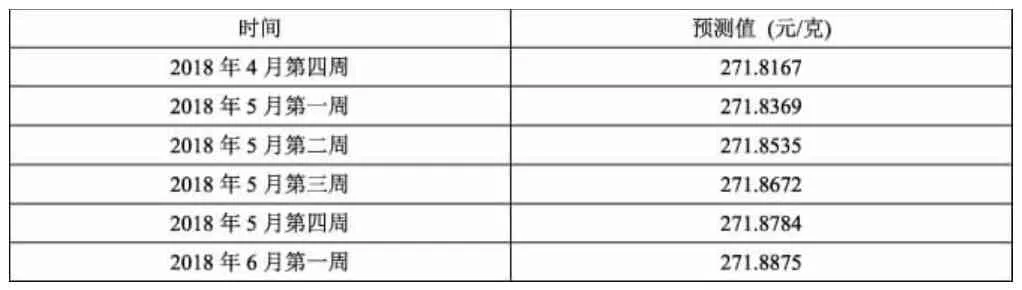
表2.4 黄金价格预测值

四、结束语

本文通过建立ARMA(1,2)模型，对黄金价格的走势进行分析及预测，得出以下结论及建议：

第一，该模型2018年3月第3周至2018年4月第3周的黄金的周平均价格预测值与实际数据相比拟合度较高，短期预测结果较为精确，该模型具有较高的应用价值。

第二，2018年上半年黄金的周平均价格将呈小幅度上涨态势，稳定在271元/克左右。这为投资者如何更准确而理性地投资黄金提供了方法和理论依据。

第三，ARMA模型对价格变化的解释能力仅为11.5%，因此如果投资者要在黄金市场进行长期投资，黄金的周平均价格的上涨幅度，更大程度上取决于石油价格、美元汇率、通货膨胀、股票价格、利率政策影响因素的变化。

第四，结合ARIMA模型对国际黄金价格影响因素基本面的分析，实际利率降低或者不变与通货膨胀预期的加深会加大国际黄金价格上涨的可能，具体的数值将取决于实际利率下降以及通胀的幅度，其他影响因素的变化可能性不大。