独塔双跨矮塔斜拉桥实用计算方法

胡陶

（浙江大学建筑工程学院,浙江 杭州 300058）

0 引言

斜拉桥结构体系主要是由塔、梁、索三种基本构件组成[1]，在很早以前人类就掌握了在塔架上悬挂斜拉索来支撑桥面体系的方法。在上个世纪70年代左右，斜拉桥在世界范围内开始应用，到了90年代发展迅速。我国的第一座斜拉桥是1975年修建的重庆市云阳县跨径76 m的预应力混凝土斜拉桥。随着桥梁理论的不断发展，以及对桥梁所处地质条件、地形地貌的限制，斜拉桥的体系越来越多样化，其中矮塔斜拉桥就是由于受到周围环境的影响而发展起来的。相对于普通的斜拉桥而言，矮塔斜拉桥具有塔身矮、主梁上跨中无索区及边跨端部无索区长度较长、边跨与中跨的比值一般在 0.45～0.70 之间[2，3]、主梁高度较高、拉索对竖向荷载的分担力小于30%、斜拉索中的应力变化幅度较小[4]、拉索倾斜角度小等特点。为了研究矮塔斜拉桥的拉索与主梁各自承担的荷载情况，许多研究者[5-7]提出了拉索荷载分担比的概念，并推算了当矮塔斜拉桥作用均布荷载时，拉索所承担荷载的公式。本文在此基础上进一步推算了当矮塔斜拉桥作用于集中荷载时，拉索所承担荷载的公式。并通过Midas有限元软件建模，验证公式的正确性,并进行了参数分析。

1 拉索索力分布情况

通过对灵江大桥、日本小田原港桥、日本蟹泽大桥进行Midas建模（拉索采用桁架单元模拟），由于结构为对称体系，因此取一半作为结构分析对象，在100 kN的集中荷载从结构一端移动到另一端，得到了拉索结构的索力分布情况，如图1～图3所示。图中的图框为某集中力位于桥梁上某处，各拉索的受力情况，以此类推，图中的每一个循环均代表了集中力位于不同位置处各拉索的受力情况。

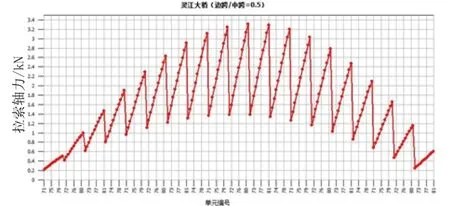
图1 灵江大桥索力分布图

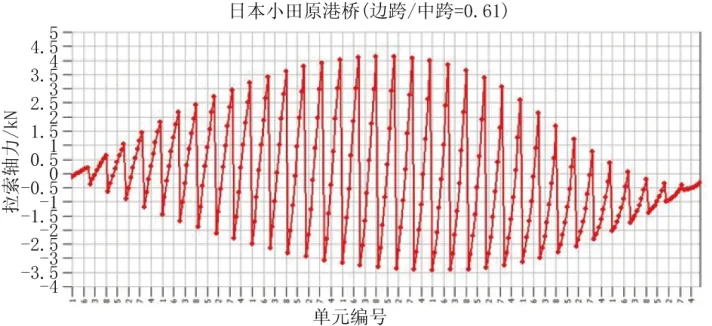
图2 日本小田原港桥索力分布图

图3 日本蟹泽大桥索力分布图

图中 的每一个波谷到波峰及为集中荷载作用于某特定位置处，尾索至靠近索塔处拉索的受力情况。从以上三幅图可以得知：对于矮塔斜拉桥而言，集中荷载作用于主梁任意位置处，从尾索到靠近搭处的拉索的索力都是接近线性分布，且对于不同的边中跨比的矮塔斜拉桥都具有这个特性。因此，假设在集中荷载作用下，拉索的竖向分力分布方程为：

2 公式推导

假设矮塔斜拉桥的塔的刚度很大，忽略塔的水平位移，且忽略由于拉索横向水平分力引起主梁刚度的变化，将独塔双跨矮塔斜拉桥的结构简化成图 4（a+b+c=1）。

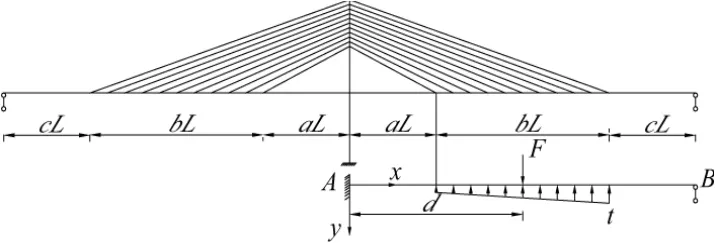
图4 独塔双跨斜拉桥简化模型

计算外荷载作用下的挠度公式。

超静定结构在作用下的挠度[8]：

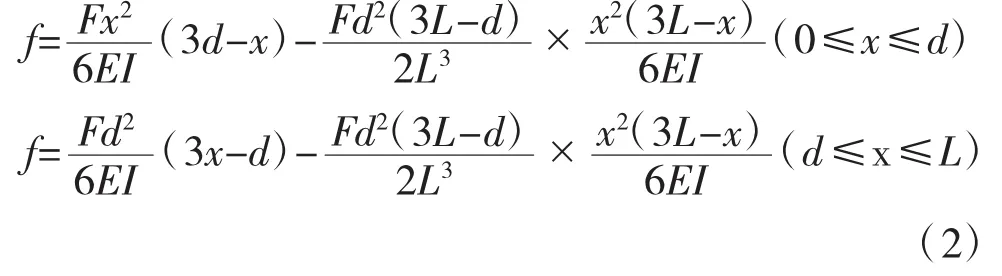
计算集中荷载位于不同区段时，aL和（a+b）L的挠度。当0≤d≤aL时：

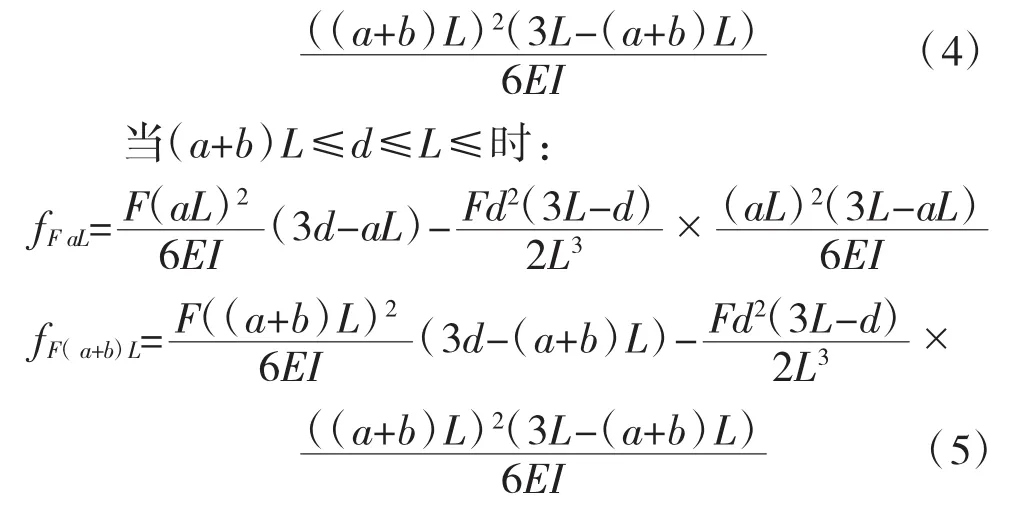
计算拉索对主梁产生的竖向力所引起aL和（a+b）L处的挠度。采用积分法（将线性分布力分成一小段的集中力）计算两点挠度：当x=aL时：

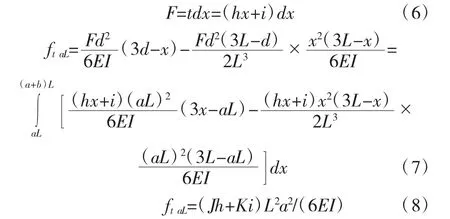
当x=（a+b）L时：

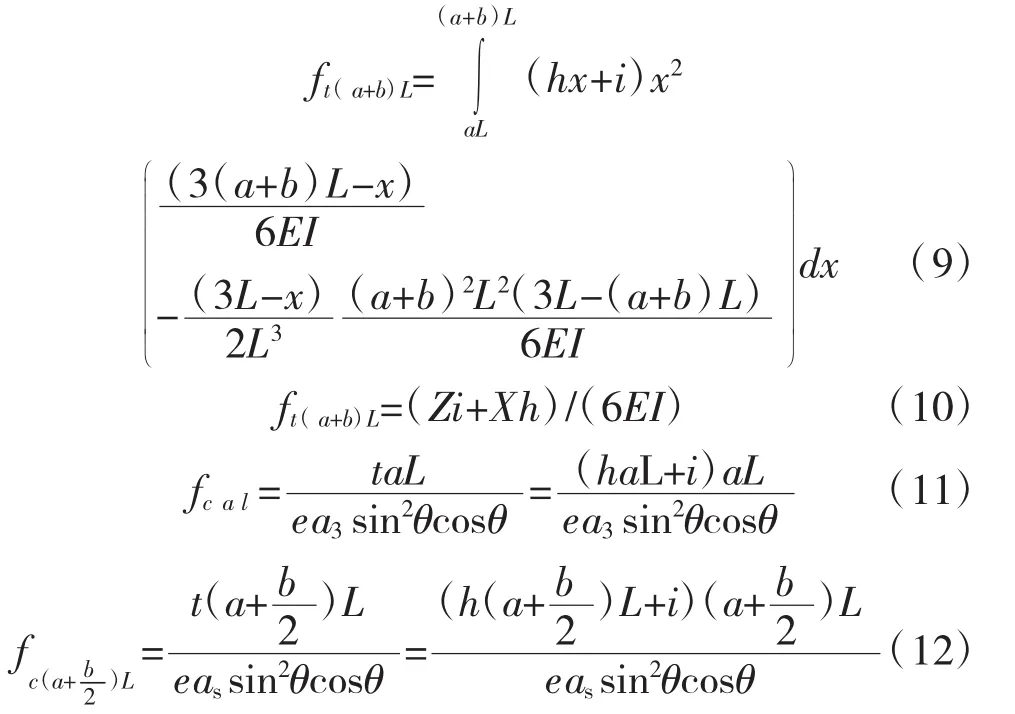
式中：θ拉索与主梁的水平夹角；eas=EsAs/g：拉索均布轴向刚度，Es、As分别为拉索的弹性模量和横截面积；g为两拉索索端之间的间距。根据x=aL，x=（a+b）L处挠度相等的关系得：

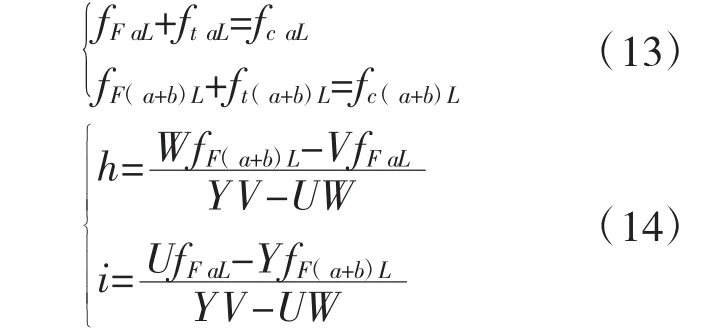
得：

3 公式验证

以灵江大桥为例，用midas建立有限元模型对推出的理论公式进行验证。将灵江大桥[9]的各参数做合理的修改，具体参数数值如下：灵江大桥为独塔双跨斜拉桥，左右两跨跨径为80 m，主塔高度为15 m，塔根处无索区长度为20 m，中间布索段40 m，主塔采用C50混凝土，主塔截面为4 m（纵桥向）2 m（横桥向），拉索间距4 m，拉索形式为平行拉索单索面，其角度为14.036°，拉索采用高强钢丝。主梁面积为20.80 m2，惯性矩为23.955 8 m4，拉索的面积为0.010 36 m2，计算模型如图5所示。

图5 独塔双跨斜拉桥简化模型

计算当荷载作用在d=18 m和d=38 m处时，各拉索t的分布情况（见表1）。

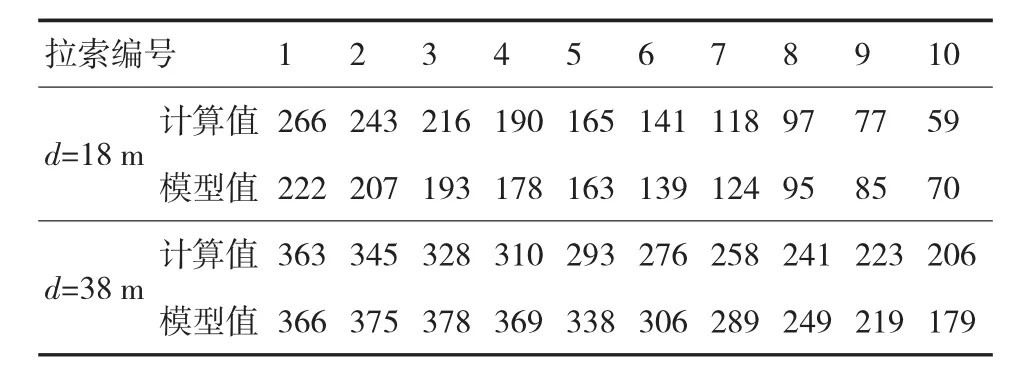
表1 本文公式与有限元计算结果比较表 10-6

表1列出了当集中荷载位于18 m和38 m处时，各拉索按上述公式计算所得的计算值，以及用midas有限元软件建模所得的模型值，通过模型值与计算值比较，在d=38 m处的平均误差为8.93%,d=18 m时的平均误差在9.15%。在结构进行概念设计时，满足精度要求。因此，在本文第二节中所推算的公式是合理的。从表1中的数据看，计算值与模型值还是有较大的误差，其主要原因有两个：（1）公式在推导过程中假设矮塔斜拉桥的主塔刚度无限大，在活荷载的作用下不发生水平位移，这与实际情况有出入；（2）拉索产生的水平分力对主梁来说形成了一种预压力，会导致主梁刚度从边界向塔根方向逐渐增大，在理论公式推导时，假设其值为一定值EI。

4 参数分析

假定公式（15）中的x为某一定值，考虑斜拉索拉索均布轴向刚度eas、斜拉索角度θ，梁截面惯性矩I对拉索荷载分担的影响。从图6中的曲线可以得知随着ea的增大t值也随之增大，且随着d值的增大这种增加趋势越显著。从图7中的曲线可以得知随着θ的增大t值也随之增大，但增加的幅度并不明显，在21°～23°之间时，增加较大，但当角增加到23°～25°时，值出现了负值，由于该结构体系拉索是索结构，认为只受拉不受压，因此，这种桥型结构体系斜拉索的倾角取值是有一定范围，并不是0°～90°，且随着d值增大，t的增加幅度更大，但当d值越大时，相邻两d值之间的增量差异越来越小。从图8中可以得知随着主梁抗弯惯性矩I的增大，逐渐减小，相邻两I之间减小的幅度在也在逐渐减小。综上几条分析结果可知，在工程上，对于矮塔斜拉桥，可以通过采取减小拉索刚度（即减小ea的值）、增大主梁的刚度的方式来减少拉索的拉力，从而可以减少拉索的应力幅值，有效地解决拉索的疲劳破坏问题，由于拉索拉力较小，也便于其在主塔或主梁上的锚固，减小了施工难度。角度变化对于拉索索力不明显，对于矮塔斜拉桥而言，在工程实践中不宜采用改变角度的方式来减小拉索索力。

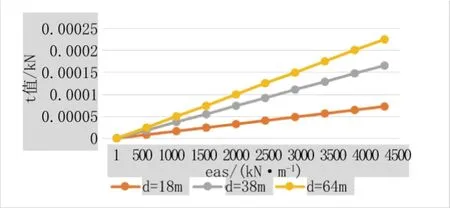
图6 eas与的关系曲线图

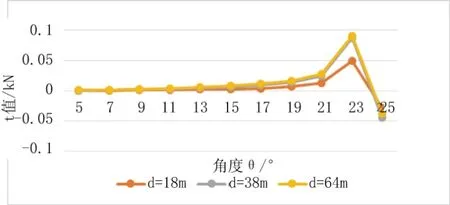
图7 θ与的关系曲线图

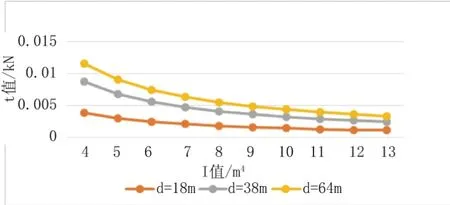
图8 I与t的关系曲线图

5 结语

本文通过简化模型，用力学公式推导了矮塔斜拉桥斜拉索在集中荷载作用下的受力情况，这对于桥梁在进行成桥实验荷载布设起到了一定的指导作用，可用于成桥荷载实验的初步设计。

本文还存在一些不足之处，例如未对理论计算公式进行系数修正，边界条件过于简化，这些都会造成理论值与实际值的偏差，有待于进一步深入研究。