基于多因素约束度函数的拆卸序列规划研究*

陈 建，胡俊康，王建勇

(浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室，浙江 杭州 310014)

0 引 言

拆卸是再制造工程的重要工序，其关键在于拆卸序列规划，高效率、高质量的拆卸序列能够使产品在生命终端时可重用部分可以得到有效的利用[1]。

目前，国内外许多专家学者对拆卸序列规划方法进行了研究，提出了一些可行的拆卸序列规划方法[2-3]。ZHANG Xiu-fen 等[4]根据装配约束、拆卸优先系数、拆卸时间因子、拆卸工具系数和组合类型因子，建立了平行拆卸的映射模型进行序列规划；WANG Heng-yu等[5]建立了一种有向约束图模型，并采用破坏性拆卸方法来优化目标拆卸序列规划；王伏林等[6]考虑拆卸过程中稳定性因素，得出了可行的最优的或近似最优的拆卸序列；PINTZOS G等[7]从产品设计文件中生成拆卸相关信息，并基于反汇编优先图生成算法，提出了一个估算拆卸过程时间的拆卸序列规划方法；VANEGAS P等[8]提出了一种eDiM方法，通过操作技术来计算操作序列的时间进一步分析可拆卸性；宋守许等[9]通过拆卸混合图表达产品零部件之间的连接关系和优先约束关系，建立了拆卸序列规划数学模型和适应度计算公式；蔡凯骏等[10]根据零件配合关系以及可拆卸性的表达，提出了以等待时间为主的拆卸序列方法；LUO Yong-tao等[11]根据产品结构建立多层表示法的动态产品数据模型，利用蚁群算法以获得最佳拆卸方案；王攀等[12]通过Petri网建立拆卸模型，并利用混沌粒子群算法进行了拆卸序列规划；MAROUA K等[13]考虑到拆卸约束不仅在产品生命周期的环境中是重要的，而且在其生命周期中也是重要的，提出了一种基于蚁群算法的自动拆卸序列规划方法；刘志峰等[14]将模拟退火粒子群优化算法应用于拆卸序列规划求解过程；HIDEYUKI N等[15]提出了一种基于遗传算法的拆卸调度方法，该方法通过拆卸多个产品的拆卸过程和后工序对拆卸零件进行拆卸和回收，从而使整个拆卸和后处理时间最小化。

上述研究中主要考虑拆卸过程中拆卸工具的使用次数、拆卸方向变换次数、两零部件拆卸时所需要的时间或者拆卸成本等因素，并选取其中一项影响因素作为拆卸序列规划的依据，从而导致生成的拆卸序列与实际操作不符。事实上在拆卸过程中，这些影响因素是共同存在的，必须综合考虑。另外拆卸时，零部件本身的外形复杂程度以及它自身重量也会在一定程度上影响拆卸序列的规划。

本文将根据零部件之间的约束关系，建立约束状态图，并根据拆卸过程中的主要影响因素，提出多因素下的综合约束度函数，并利用粒子群算法实现生命终端产品的最优拆卸序列生成。

1 多因素下约束度函数的构建

1.1 拆卸模型的建立

拆卸序列规划的基础是建立拆卸模型[16]。产品是由零部件以一定的约束关系组成结构稳定且具有特定功能的装配体。通常，设约束状态图G=(V,L)为顶点和连接这些顶点的线(边)的集合，其中：V=(v1,v2,…,vN)—图中所有节点的集合，为一个有限集；N—最小拆卸单元(零件或子装配体)个数；L=(l1,l2,…,lm)—图中所有边的集合，也是有限集，表示两顶点之间存在约束关系，用直线表示；M—约束关系的数量。约束状态示意图如图1所示。

图1 约束状态示意图

1.2 零部件的外形描述

本研究根据零部件的基本外形尺寸以及零件的质量，对零部件外形复杂程度进行量化处理，再通过对加工方式和零部件类型的不同进行分类描述。

切削加工是机械制造中最主要的加工方法。若零件的外形尺寸越复杂，加工量越多，则去除的材料越多，因此通过计算毛坯与零件的质量比可以形象地描述零件的形状复杂程度，即形质比。若零部件外形越复杂，则形质比越大；反之零部件外形越简单，则形质比越小。

各类切削加工件形质比示意图如图2所示。

图2 切削加工件形质比示意图

图中，透明框部分为拟合加工之前的毛坯，实体部分为加工完成之后的零件。

铸件的零件表面较为复杂，箱体类和叉架类零件多为铸件，可以通过拟合一个毛坯的方式用于计算零件的形质比。

各类铸件类形质比示意图如图3所示。

图3 铸件类形质比示意图

图中，透明框部分为拟合毛坯，实体部分为加工完成之后的零件。

其中，箱体类零件主要由钣金件或者简单杆件构成，加工制造方法简单，钣金件和杆件重量也都比较轻。但箱体类零件多为其他零件安装的基础零件，可将其视为机架部分，多为不拆卸部分或者最后拆卸部分，因此根据拟合的毛胚计算形质比。对于机架而言，形质比应越大越好。

通过拆卸物元的参数化模型，可以得知最小拆卸单元的外围形状尺寸、材料密度以及最小拆卸单元的质量，则形质比可表示为：

(1)

式中：d—轴套类、盘盖类毛坯的直径；h—轴套类、盘盖类毛坯的高；a,b,c—其他类型毛坯的长、宽、高；ρ—零部件材料密度；M—零部件的实际质量。

若形质比越大，则零部件外形越复杂，拆卸时的难度也越大；若形质比越小，则零部件外形越简单，拆卸时的难度也越小。

举例：两板件类零件的毛坯长、宽、高都为30 mm、30 mm、7 mm，材料45钢，但是两零件所打的孔个数不同，分别计算这两零件的形质比。

两板件类形质比示例图如图4所示。

图4 两板件类形质比示例图

得到η1<η2，零件2的形质比大，因此零件2的外形相对更复杂。

1.3 零部件的拆卸距离

在整个产品中，各个拆卸单元的位置都是不同的，通常拆卸过程都是由外到内或者由一侧开始到另一侧结束，因此各个零件的相对位置影响拆卸顺序。在建立拆卸模型的时候，通常会选择一个不拆卸零部件或者最后拆卸零部件作为约束状态图的起点，即零部件1。因此，在计算各个零件的相对位置时，笔者将约束状态图起点处的零部件定为中心件，以该零部件的几何中心为基准计算各个待拆卸零部件的几何中心到基准的距离，即拆卸距离。零部件拆卸距离示意图如图5所示。

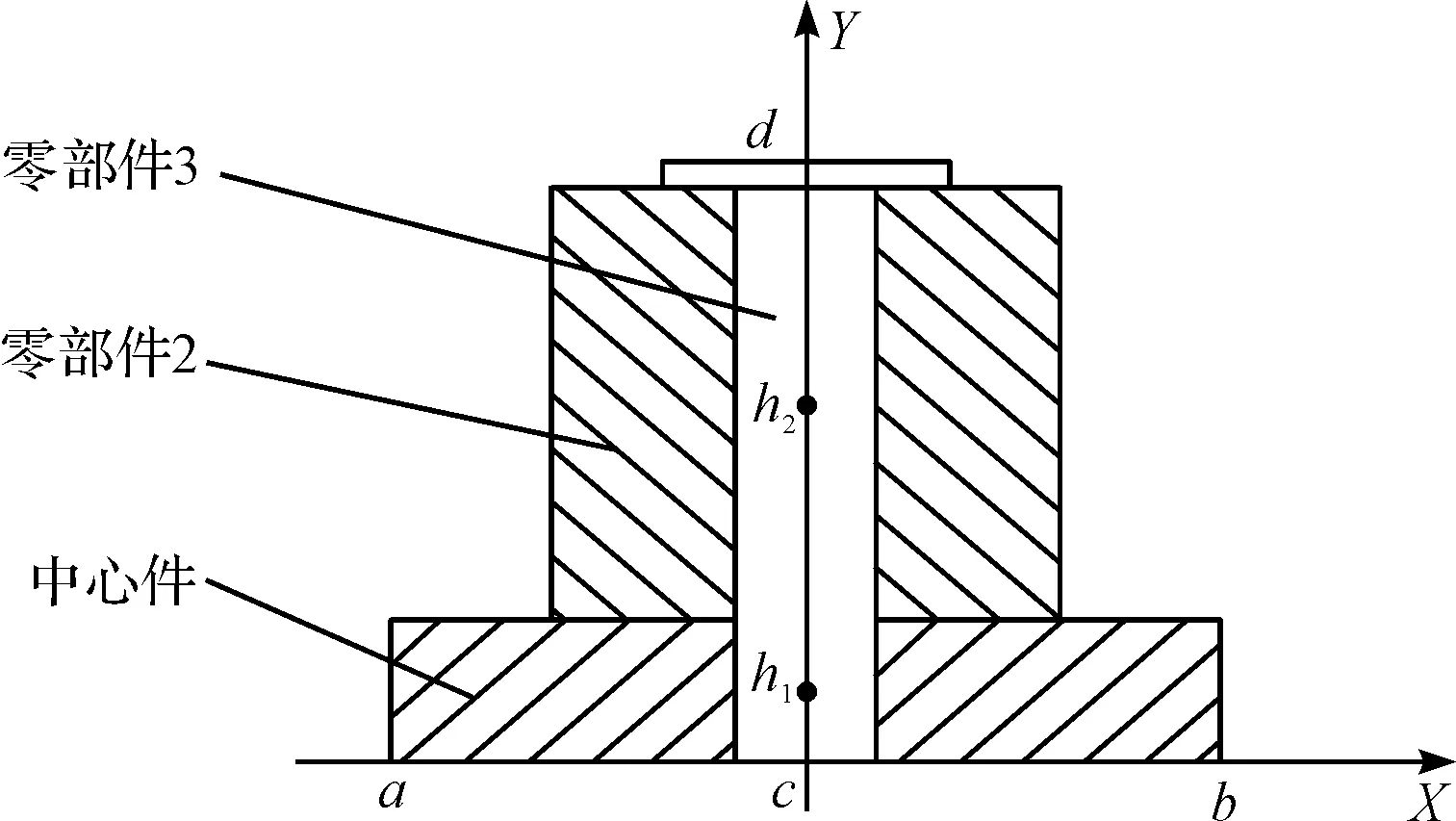
图5 拆卸距离示意图

本研究以对称轴为基准建立坐标系，在X轴上待拆卸产品的外形尺寸区间为X0=〈a,d〉；Y轴上待拆卸产品的外形尺寸区间为Y0=〈c,d〉。其中：h1(x1,y1)—中心件的几何中心；h2(x2,y2)—待拆卸零部件2的几何中心。则待拆卸零部件2与中心零部件1的拆卸距离为：

(2)

根据拆卸序列规划原则，往往中心件是在中心或者一侧，可知拆卸物元的距越大，则距离中心件也越远，因此优先拆卸。

1.4 拆卸成本

约束关系的解除以及联接件的拆卸需要拆卸工具，本研究依据拆卸力、拆卸难度和拆卸消耗，在约束关系元中把拆卸工具分为几类，如表1所示。

表1 拆卸工具分类表

在拆卸完成后，因零部件间的约束关系、拆卸方式、拆卸工具不同，从而导致拆卸后的零部件会产生不同程度的损伤或者破坏。依据拆卸之后零部件再次利用的方式，将拆卸级别分为几类，如表2所示。

表2 拆卸级别分类表

拆卸成本是衡量拆卸可行性的重要判据。拆卸成本主要由人工成本和拆卸工具消耗成本组成。其中，人工成本包括拆卸时间和单位时间工资水平，拆卸时间又可分为拆卸工具准备时间和拆卸操作时间。拆卸工具消耗成本则主要与拆卸工具的价格和使用寿命(按使用次数)有关，此外还包括使用电力驱动所产生的能耗问题。因此，拆卸成本为：

C=TdisSw+Cr

(3)

式中：Tdis—拆卸时间；Sw—单位时间工资；Cr—拆卸工具消耗成本。

拆卸时间为：

Tdis=Tij×Nk

(4)

式中：Ti,j—单次常规拆卸零部件i与零部件j之间约束所需的拆卸时间；Nk—零部件i与零部件j之间约束数量。

拆卸工具消耗成本为：

(5)

式中：Cm—常规拆卸工具价格；Ne—常规拆卸工具的额定寿命(按使用次数)；Pelec—电动常规拆卸工具的功率；To—电动常规拆卸工具随需的拆卸时间；Cd—使用地的电价。

在一定程度上，本文给出的一些具体量化数值是一个平均值。在拆卸时间方面，可根据不同连接情况下得到所需的拆卸时间，单位时间工资根据当时工资水平来获取。

常用拆卸工具参数以及不同拆卸级别的单次拆卸时间如表(3，4)所示。

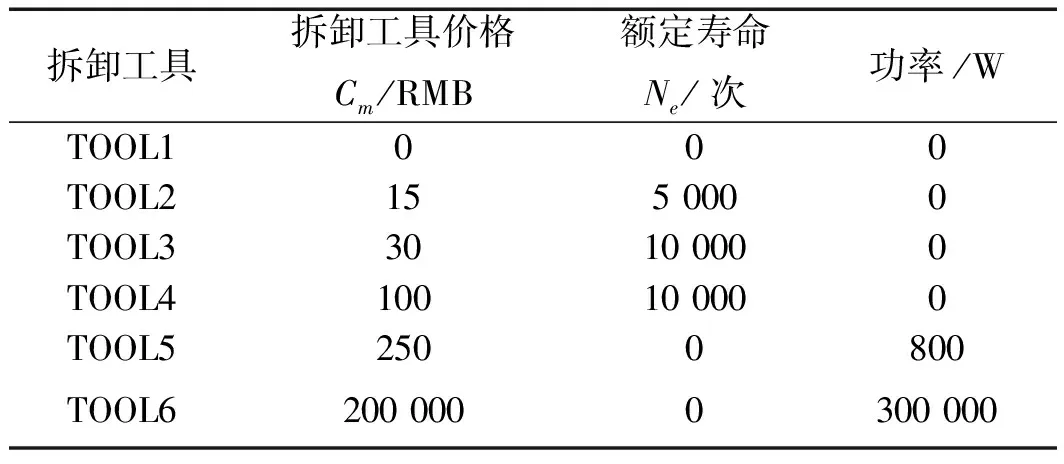
表3 常用拆卸工具参数表

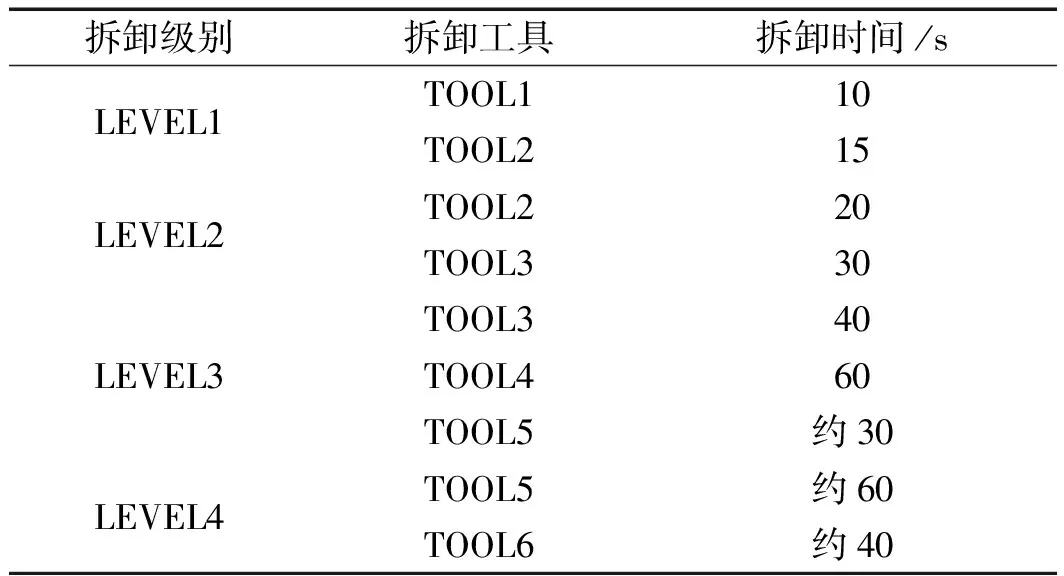
表4 拆卸级别和拆卸工具对应的单次拆卸时间表

1.5 综合约束度

1.5.1 拆卸距标准化处理

对于拆卸距，拆卸距越大，则距离中心件越远，相应的拆卸性越好；反之拆卸距越小，则拆卸难度越大，属于负类属性影响因数。此处利用极差标准化法对拆卸距进行标准化，即:

(6)

式中：ρi—拆卸距。

经过极差标准化法后，拆卸距越大，则k1越小；反之，k1越大，并且k1∈[0,1]。

1.5.2 拆卸成本标准化处理

对于拆卸成本，拆卸成本越大，则拆卸所消耗的人力物力也越大；反拆卸成本越小，则拆卸所消耗的人力物力也越小，属于正类属性影响因数。此处利用极大值标准化法对拆卸成本进行标准化，即:

(7)

式中：ci—拆卸成本；∑ci—整个产品的拆卸成本。

经过总和标准化法后，成本k2越大，则越大；反之，k2越小，并且k2∈[0,1]。

1.5.3 约束度函数的构建

约束度函数是一种对拆卸约束的综合度量，记为ki,j(i，j—拆卸对象标号)。根据约束度函数的定义，两零部件拆卸越困难，则约束度函数越大；拆卸越简单，则约束度函数困难。因形质比、拆卸成本越大，则零部件拆卸越困难，因此与约束度函数成正相关关系；拆卸距离越大，则零部件拆卸越困难，因此与约束度函数成负相关关系；无约束关系约束度函数可设置为0。因此，建立一个综合约束度函数如下：

(8)

式中：ηi—零部件i形质比；α1,α2—比例系数，且α1+

α2=1；α3—修正系数。

根据约束状态图模型，笔者利用上述综合约束度计算公式，可得综合约束度矩阵：

M=(ki,j)N×N

(9)

式中：N—最小拆卸单元个数；M—N阶矩阵。

根据图1所示约束状态图模型，可得到约束状态矩阵为：

2 基于粒子群算法的拆卸序列生成

1995年，KENNEDY和EBERHART[17]首次提出粒子群算法(PSO)，这是一种新的群体智能算法。

2.1 粒子初始化

粒子群的初始化是问题求解的关键。粒子i的位置Xi=(xi1,xi2,…,xin)表示产品中所有需要拆卸的零部件的排列组合，即一个拆卸序列。其中：n—粒子的维数，即某一产品中零部件的总个数;xij—粒子i的第j维分量，表示零件的编号，即拆卸序列i中进行拆卸的第j个零件的编码。粒子的初始位置，即初始拆卸序列是随机生成的。粒子i的速度Vi=(vi1,vi2,…,vin)用以改变粒子的位置，与粒子位置的维数相同。

2.2 粒子的位置速度进化规则

拆卸序列规划问题属于离散型组合优化问题。为了针对具体问题进行分析，本研究将速度与位置更新公式中的运算法则进行重新定义。相应运算法则重新定义如下：

(10)

(11)

(12)

vij(t+1)=

(13)

Xi(t+1)=Xi(t)+Vi(t+1)

(14)

式(10～14)中：a—随机数且a∈(0,1)；p—个体极值；g—全体极值。

在更新粒子的位置时，若速度Vi(t+1)中的元素vij(t+1)=1，则不改变位置拆卸序列Xi(t+1)中第j维对应的零件号，即xij(t+1)=xij(t)；若速度Vi(t+1)中的元素vij(t+1)=0，则将拆卸序列Xi(t+1)中的第j维对应的零件号与第j+1维对应的零件号交换位置，即xij⟺xi(j+1)。由于粒子位置与速度的维数相同，此位置更新公式保证了Xi(t+1)的维数仍然是n。

根据以上重新定义的运算法则，通过一例子具体说明其运算过程。

设Xi(t)=(6,5,3,4,2,1)，Pi(t)=(6,4,5,3,2,1)，G(t)=(6,5,4,3,2,1)，Vi(t)=(1,0,0,0,0,0)，则计算过程如下：

Pi(t)-Xi(t)=(6,4,5,3,2,1)-(6,5,3,4,2,1)=(1,0,0,0,1,1)；

G(t)-Xi(t)=(6,5,4,3,2,1)-(6,5,3,4,2,1)=(1,1,0,0,1,1)；

Vi(t+1)=Vi+(Pi-Xi)+(G-Xi)=(1,0,0,0,0)+(1,0,0,0,1,1)+(1,1,0,0,1,1)=(1,1,0,0,1,1)；

Xi(t+1)=Xi(t)+Vi(t+1)=(6,5,3,4,2,1)+(1,1,0,0,1,1)=(6,5,4,3,2,1)。

2.3 粒子适应度函数

拆卸序列规划的目的是得到拆卸最简单和拆卸消耗最少的可拆卸序列。本研究通过对各个拆卸影响因素进行全面的分析和量化处理，并建立综合约束度函数和约束度矩阵。根据综合约束度函数和约束度矩阵，将适应度函数定义为：

(15)

式中：sum(Dxi(j-1)MDxi(j-1))—计算矩阵Dxi(j-1)中第xij行所有元素之和。

在粒子群更新过程中，粒子的适应度函数值越低，表示得到可拆卸序列的拆卸方法最简单和消耗最少，因此拆卸序列越优。

则拆卸xij的拆卸算子Dxi(j-1)可表示为：

例如：

计算xij=2的适应度大小为：sum(Dxi(j-1)MDxi(j-1),xij)=6。

2.4 拆卸序列规划

利用粒子群优化算法进行产品拆卸序列规划，其本质是将基于图搜索和智能算法相结合。拆卸序列规划具体步骤如下：

(1)对产品的模型进行预处理，提取零部件之间的约束关系，根据这些约束关系建立约束状态图；

(2)计算各个零部件的外形复杂程度及其拆卸距离，并根据拆卸工具和拆卸级别计算出拆卸成本；

(3)利用综合约束度函数得到约束度矩阵；

(4)利用粒子群算法生成最优拆卸序列。

拆卸序列规划算法流程如图6所示。

图6 拆卸序列规划流程

3 实验及结果分析

平口钳是一种通用可调夹具，由于其定位精度较高、夹紧迅速、通用性好、操作方便而得到广泛应用。平口钳是亦损亦耗品，研究对平口钳进行拆卸回收具有重要意义。

平口钳装配示意图以及对应的约束状态图如图(7，8)所示。

图7 平口钳装配示意图1—固定钳身；2—螺杆；3—钳口板；4—活动钳身；5—紧固螺钉；6—螺母；7—固定圆环

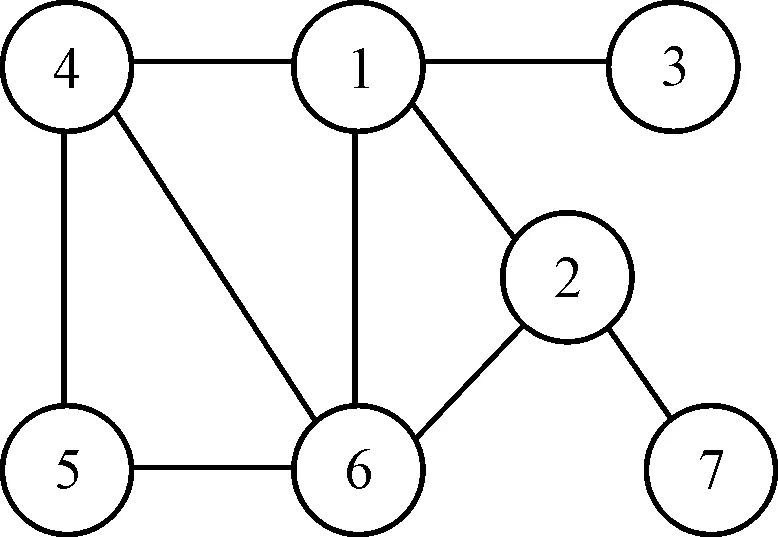
图8 平口钳约束状态图

本研究根据公式(1～3)计算各个零部件的外形复杂程度及其拆卸距离，并根据拆卸工具和拆卸级别计算出拆卸成本。

各个零部件对应的形质比如表5所示。

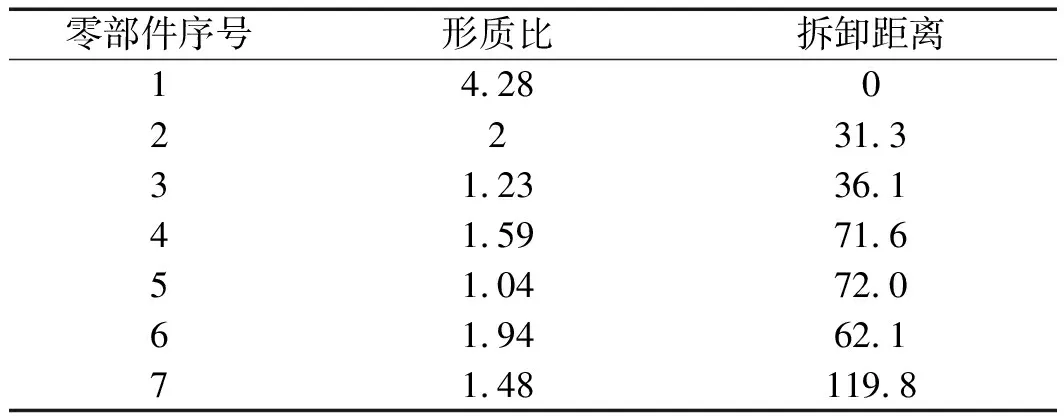
表5 零部件的形质比

各个约束关系对应的拆卸成本如表6所示。

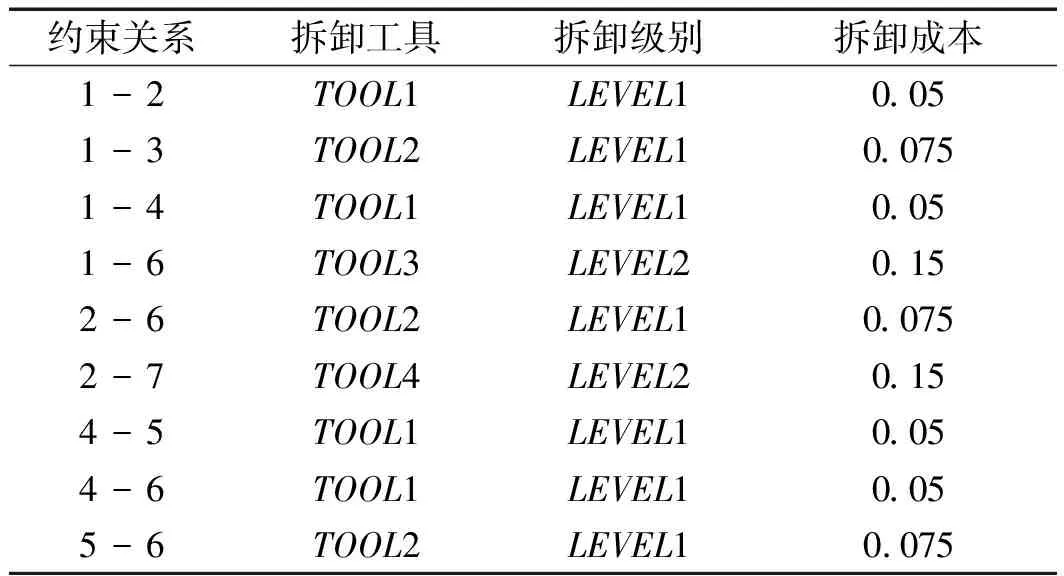
表6 约束关系的拆卸成本

根据公式(5,7,9)，取α1=0.4,α2=0.6,α3=1，可得到约束度矩阵：

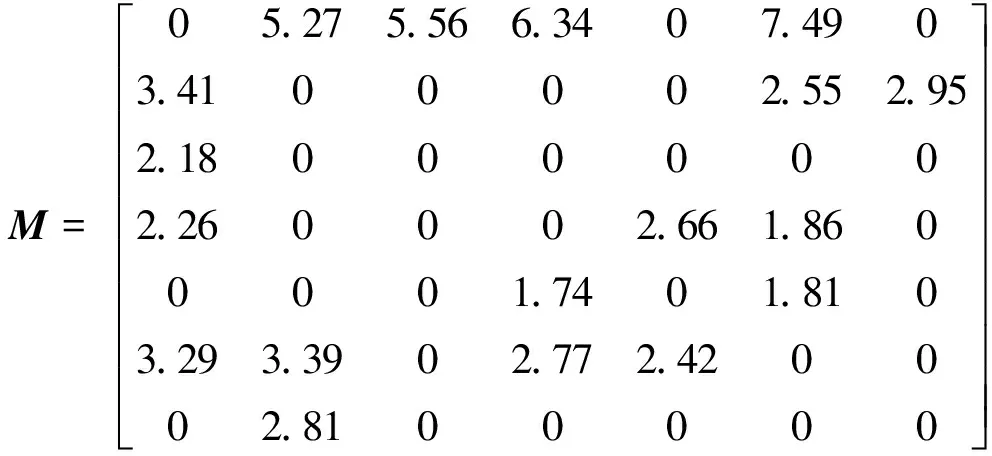
最后在PSO中取惯性权重ω=1，加速常数c1=c2=2，种群规模为10，利用粒子群算法进行拆卸序列生成，可得到最优拆卸序列为3-7-2-5-4-6-1。

粒子群收敛过程如图9所示。

图9 粒子群收敛过程

4 结束语

通过分析零部件间的约束关系，本文建立了约束状态图拆卸模型，并根据零部件的外形复杂程度，提出了形质比的概念以及计算公式来理想化描述零部件外形复杂程度以及产品的一般拆卸过程，建立了拆卸距离的计算方法，用于描述零部件之间的相对位置；另一方面利用了拆卸成本的计算公式，对拆卸工具和拆卸级别进行了统一换算；在对上述的影响因素的量值进行标准化处理后，构建了多因素下的约束度函数和约束度矩阵，然后重新定义了粒子的位置速度进化规则，利用约束度矩阵构建了粒子适应度函数，并用粒子群生成拆卸序列。

研究结果表明：该拆卸序列规划方法降低了拆卸序列生成的复杂程度，减少了拆卸序列规划的工作量。目前该方法还处在人工拆卸阶段，在今后的研究中，将结合机器视觉实现智能拆卸。