磁流变阻尼器输出阻尼力灵敏度分析*

安晨亮，马金玉，王嘉维，权凌霄*

(1.北京航天发射技术研究所，北京 100076；2.北京精密机电控制设备研究所，北京 100076；3.燕山大学 机械工程学院，河北 秦皇岛 066004)

0 引 言

振动是普通工业、航空航天等装备领域中普遍存在的现象[1-2]，如果得不到有效控制，会严重影响装备的寿命及可靠性，因此，振动控制技术研究十分重要[3]。

振动控制可以分为被动控制、主动控制、半主动控制和混合控制4类。近年来，随着智能材料的快速发展，利用记忆合金、压电陶瓷、电流变液及磁流变液等智能材料实现半主动振动控制逐渐得到重视，并形成了很多应用成果[4]。

磁流变阻尼器以磁流变液为主要阻尼材料，其结构简单、响应速度快、阻尼力控制范围较大，能够适应宽频振动信号的控制，且不需要过多的外部能源接入，具有更好的控制效果，并逐步得到广泛应用[5]。虽然国内外学者对磁流变阻尼器原理，流变特性的研究和开发磁流变液新的应用等方面取得了丰硕的成果，但其输出阻尼力变化对每一个的设计参数变化敏感程度的研究还较少。影响磁流变液输出阻尼力的参数很多，其中包括阻尼器控制电流、活塞运动速度、励磁线圈的匝数、活塞的有效长度等因素，依据实际工况条件，定性地分析每个参数对磁流变阻尼器输出阻尼力的影响，并定量地掌握所有参数对阻尼特性的影响，结合结构参数优化理论，可得到磁流变阻尼器结构参数优化方法[6-7]。

磁流变阻尼器的数学模型较为复杂，采用传统的分析方法难以反映出其非线性问题，使得各参数的定量分析结论难以获取。灵敏度分析首先应用在数学领域中，主要用于分析参数变化引起微分方程解的变化。具体的分析方法是：将微分方程组的特征值、特征向量作为含有参数的多元函数，直接将它们对参数进行微分运算[8-9]。由于现代控制理论发展的需要，在诸多控制领域中引入灵敏度分析，研究外干扰对系统性能的影响，并取得了很好的分析效果。灵敏度分析是一种能定量分析系统各参数变化对系统特性影响权重的有效方法，将其运用于磁流变阻尼器能够很好地解决这一难题。

本文将一阶和二阶输出灵敏度应用于磁流变液振动控制系统的分析中，建立磁流变液输出阻尼力的数学模型，研究一阶和二阶输出灵敏度分析方法理论模型，进而求解出一阶和二阶输出灵敏度分析方法的表达式，对比活塞运动速度和控制电流等10个参数灵敏度分析结果的异同点，进行理论分析，得出10个参数对输出阻尼力的影响程度。

1 磁流变液输出阻尼力的数学建模

1.1 研究对象

磁流变液阻尼器结构图如图1所示。

图1 磁流变液阻尼器结构图

当活塞内的励磁线圈通入电流时，在活塞头内部的导磁体会产生磁场，贯穿环形阻尼孔到外套筒再返回到活塞中，形成一闭合磁路。此时流经环形阻尼孔内的磁流变液发生磁化，致使活塞运动时产生较大的剪切屈服应力，从而形成一定的阻尼力，通过控制磁流变液阻尼器的电流可用来控制阻尼力大小。

为了得到更多影响磁流变液输出阻尼力的参数，本文采用的数学建模方法以伪静力模型和Bingham模型为基础。为了计算方便，减少变量数，进行简化：

(1)认为磁流变液不可压缩；

(2)认为温度对阻尼器性能影响很小；

(3)认为零场作用时磁流变液具有较低的黏度；

(4)认为铁芯材料不存在剩磁，磁滞回线包含面积小，矫顽力低，且无涡流损失和磁滞损失。

1.2 流体微分方程推导

磁流变液流变特性可简化为在两相对运动的平板之间的流动，平板模型如图2所示。

图2 环形间隙中的流速分布图g—两平板之间的间隙；v—平板的相对运动速度

本研究建立如图2所示的坐标系，磁流变液以体积流速Q在x方向上一维流动，在y方向不流动，由流体力学可得出微分方程：

(1)

式中：u，v—磁流变液在x,y方向上的流动速度；∂σxx/∂x—磁流变液在x方向的压力梯度；ρ—磁流变液的密度；t—时间变量。

为了简化，将压力梯度简化为x方向按线性变化，则得到∂σxx/∂x=-Δp/l；当流动速度较低时，可不计惯性效应，则有∂u/∂t=0；令沿x方向的剪切应力τyx=τ，由于磁流变液流动的连续性，沿x方向的速度不变，则有∂u/∂x=0。

通过以上简化，基于平面Poiseuille流动[10]，可将式(1)简化为：

(2)

式中：l—阻尼通道的长度；Δp—阻尼通道两端的压差。

1.3 Bingbam流体流动分析

在外加磁场作用下，磁流变液表现为Bingham流体，在平行板间流动时，则有:

(3)

理论上剪切屈服强度与磁感应强度可近似描述如下[11]：

τy=152B-11.4

(4)

在平板模型中，磁流变液受到的剪切应力沿平板间隙是按线性分布的，因此，可以将磁流变液的流动分为3个区域，其流动速度分别用u1、u2和u3表示，其边界条件分别为：

在区域①中，将τ代入控制微分方程(2)可得：

(5)

由边界条件求解式(5)，可得到区域①的流速为：

(6)

同理，可求得区域②的流速为：

(7)

区域③的流速为：

(8)

利用控制微分方程(2)与边界条件：τ(g/2)=0，求解出磁流变液剪切应力的分布为τ=Δp/(2l(2y-g))。

由τ(y1)=-τy，τ(y2)=τy，可得：

(9)

(10)

刚性流动区的厚度δ为：

双及物构式(双宾构式)是指在句法层面的动词能同时携带间接宾语和直接宾语的语言形式，其结构可以码化为［NSVN1N2］。双及物构式的基本意义可以表述为“客体实际的、成功的转移”，也就是“客体从初始领有者被传递给最终领有者的过程”。这就要求进入双及物构式的动词必须具有“给予”义，必须能支配三个名词性成分，动词后的“N1”应该是有生命的。但是我们发现，许多非“给予”类、非“三价”动词也能进入双及物构式；处于“N1”位置上的名词也并非都是有生命的，这其中一定有什么因素在起作用，本小节就拟探讨这个问题。

(11)

引入一个非量纲因子，即：

(12)

再将式(12)代入式(9，10)中，可得：

(13)

(14)

两平板间隙中的磁流变液的体积流量Q关系式为[12]：

(15)

令：

根据流体力学连续性原理，磁流变液阻尼力为：

F=-ΔpA

(16)

并有以下关系式：

Q=Av

(17)

式中：A—活塞作用面积，A=(π/4)(D2-d2)，b=π(D+g)

1.4 磁路计算

为了简化计算，假设阻尼器铁芯的磁导率为一定值，并忽略漏磁效应和摩擦损失。

磁路的磁阻Rm，磁通φ和磁势Ff有以下关系：

Ff=Rmφ

(18)

磁势Ff又可以表示为：

Ff=NI(AT)

(19)

式中：N—线圈匝数；I—励磁电流

磁感应强度关系式为：

B=μH

(20)

式中：B—磁感应强度；μ—铁芯磁导率。

磁通量公式为：

φ=BS

(21)

式中：S—铁芯的横截面积。

综合(18～21)，可得出磁场强度：

(22)

假设磁路平均长度为L(m)，相对磁导率为μR，则磁阻Rm可以表示为：

Rm=L/(μS)=(l/(μRμ0S))(AT/(Wb))

根据阻尼器铁芯的结构特点，将磁路分为3个部分进行分析[13]，导磁体磁阻计算图如图3所示。

图3 导磁体磁阻计算图

区域①、区域②与区域③组成导磁体，与工作间隙组成闭合磁路。磁流变液的线圈电流是由励磁电流和铁损电流组成，当振动频率不大时可将线圈电流看成励磁电流，各区域的磁阻为：

(23)

(24)

(25)

磁流变液的磁阻近似为：

(26)

式中：μr—工作缸材料的磁导率；μMR—磁流变液的相对磁导率，μMR=2.5。

总磁阻可近似为：

Rm=Rm1+2Rm2+Rm3+RMR

(27)

综上所述，可以得到阻尼力公式：

H3F3+H2F2+H1F+H0=0

(28)

其中：

H3=-((9/4)bg3-(3/2)ηbg3-6Avlη2-3blgvη2)/A3，

H2=((15/4)blτyg2+(13/4)bηlτyg2-(3/2)bηg3-

6bvτyl2η2)/A2，

2 磁流变液输出阻尼力一阶灵敏度

2.1 一阶灵敏度函数推导

本文主要分析磁流变液输出阻尼力对系统模型中10个参数的输出灵敏度。系统各参数的输出灵敏度方程的表达式为：

(29)

α取10个参数，即：α=[α1,α2,α3,α4,α5,α6,α7,α8,α9,α10]。

其中：磁流变液阻尼器控制电流α1和活塞运动速度α2可影响最终输出阻尼力，其值可以根据实际工况而调整；励磁线圈匝数α3、铁芯的横截面积α4，铁芯的磁导率α5和磁流变液表观粘度系数α6，均会影响剪切屈服应力，进而影响输出阻尼力的大小；外筒和活塞杠之间的间隙α7，活塞阻尼环内径α8的大小，活塞轴直径α9的大小和活塞的有效长度α10的设定均会影响输出阻尼力的大小。

笔者对阻尼力方程(28)中的阻尼力F对各参数α求一阶偏导，通过Matlab软件的仿真计算，可得到各参数的一阶输出灵敏度函数：

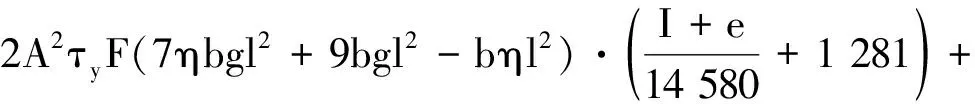
(30)

式中：A—活塞作用面积，b=π(D+g)；τy—磁致剪切屈服应力；η—磁流变液表观粘度系数；I—磁流变液控制电流；g—外筒和活塞杆之间的间隙；v—活塞运动速度；l—活塞有效长度；F—磁流变液输出阻尼力。

由于篇幅有限，本文仅给出控制电流的一阶输出灵敏度函数。

2.2 一阶灵敏度函数仿真

基于计算出的一阶输出灵敏度方程，本研究在Matlab软件主界面中进行编程。磁流变液输出阻尼力输出灵敏度函数曲线如图4所示。

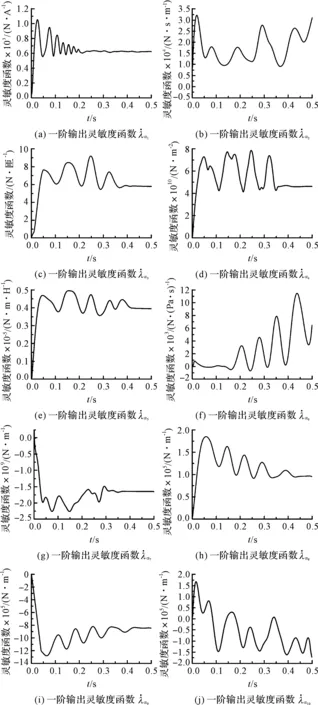
图4 各参数的输出灵敏度函数曲线图

从图4中可以看出：α2、α6和α10都会对系统输出阻尼力变化产生影响[14]，其他7个参数在整个调整时间内都对系统动态产生较大影响，对系统稳态影响相对较小，在采样时间末会趋于稳定。α2的变化会引起阻尼器内高压腔流至低压腔流量的变化从而导致阻尼力的变化，α6的改变会增加零磁场强度时的输出阻尼力，α10的增加能使得磁流变液流过的阻尼孔长度变大而增加阻尼力，使磁阻变大导致磁场强度降低，进而导致磁流变液的剪切力减小，因而这3个参数都能持续对系统稳态造成影响，最终没有趋于稳定。而其余参数的变化对系统稳态影响相对较小，在采样时间末趋于稳定。

2.3 一阶输出灵敏度分析

图4中，一阶输出灵敏度函数时程曲线描述了参数α对磁流变液阻尼器输出阻尼力F影响的动态变化过程，为量化参数α变化对阻尼力F变化的影响程度，定义两种灵敏度衡量指标。

将磁流变液阻尼器输出阻尼力的变化量ΔF与参数变化之前最大阻尼力的百分比，用于衡量各个参数变化对阻尼力F的影响程度。该百分比的表达式为：

(31)

本研究把该百分比的最大值定义为峰值灵敏度指标，用s1表示，其表达式为：

(32)

(33)

通过定义两种灵敏度衡量指标，可定量分析参数α的变化对磁流变液阻尼器输出阻尼力F的影响程度。

根据式(31)计算得出各参数变化10%时，采用柱形图的方式表达参数的一阶输出灵敏度的峰值灵敏度指标和均值灵敏度指标量化结果，如图5所示。

图5 各参数灵敏度指标

从图5中可以看出：

(1)励磁线圈匝数α3、铁芯的磁导率α5和外筒和活塞之间的间隙α7所占比例较大，峰值灵敏度指标数值在40%以上，均值灵敏度指标数值皆大于60 N，可以看出这3个参数变化10%，可以使阻尼力的变化很大；

(2)铁芯的磁导率α5的两项灵敏度指标都很大，在设计磁流变液阻尼器时要首先考虑的因素，特别是其峰值灵敏度指标数值很大，说明该参数可以使得阻尼力变化瞬间变得很大，为避免阻尼力过大损坏磁流变液阻尼器，所以在选用磁芯材料时应该将铁芯的最大磁导率作为选择材料的主要依据。同时，励磁线圈匝数α3和外筒和活塞之间的间隙α7的两项灵敏度指标都很大，其参数也是在设计磁流变液阻尼器时需要着重考虑；

(3)由于文章篇幅有限，当参数变化1%和20%时，参数变化引起的输出阻尼力变化趋势与参数变化10%结论相同。

3 磁流变液输出阻尼力二阶灵敏度

3.1 二阶灵敏度函数推导

由于本文只为求解得出单个参数对阻尼特性的影响权重，将阻尼力F对参数α的二阶输出灵敏度函数定义为：

(34)

其物理意义为参数αi的变化对参数αi的变化引起的阻尼力F的变化率的变化产生的影响，亦即αi对∂F/∂αi产生的影响。

为对比一阶灵敏度的分析结果，二阶输出灵敏度函数求解的仿真条件与一阶求解时相同，在Matlab主界面中进行编程，基于二阶输出灵敏度特殊表达式(34)计算得出灵敏度函数。对阻尼力方程(28)中的阻尼力F对个参数α求二阶偏导，可得到各参数的二阶输出灵敏度函数：

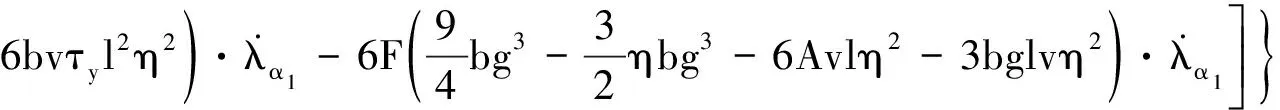
(35)

3.2 二阶灵敏度函数仿真

磁流变液输出阻尼力二阶输出灵敏度函数曲线如图6所示。

从图6可以看出：除了活塞运动速度α2、磁流变液表观粘度系数α6和活塞的有效长度α10在采样时间内对系统的动态与稳态均产生影响之外，其他7个参数在整个调整时间内都对系统动态产生较大影响，在采样时间末开始趋向于平稳，这与一阶输出灵敏度分析结果相近。

二阶输出灵敏度分析方法的两项灵敏度衡量指标可表示为：

(36)

(37)

为研究其与一阶输出灵敏度分析方法的异同点，笔者将参数变化10%，将得到的系统各参数的两项灵敏度对比柱形图合并，如图7所示。

图6 各参数的输出灵敏度函数曲线图

图7 参数变化10%两项灵敏度指标对比柱形图

从图7中可以看出：

(1)励磁线圈匝数α3、铁芯的磁导率α5和外筒和活塞之间的间隙α7对阻尼力变化最大值的百分比较大，该结论与一阶输出灵敏度分析方法所得结果相吻合；

(2)一阶输出灵敏度的两项灵敏度衡量指标值与参数变化量成正比关系，而当考虑二阶输出灵敏度时，两项灵敏度衡量指标值却与参数变化量不成成正比关系，这是泰勒展开式决定的；

(3)两种灵敏度分析方法根据两项灵敏度衡量指标，量化所得结果变化规律是相似的。二阶输出灵敏度分析方法虽然相比一阶输出灵敏度分析方法精度更高，但是其求解难度大为提高，并且考虑到当参数变化较小时，两种灵敏度分析结果较为相近，所以当参数变化量较小时可只求解一阶输出灵敏度，得到参数对系统的影响程度。然而当参数变化量较大时，必须考虑二阶泰勒展开式的影响。因为一阶泰勒展开式能大概分析出各参数对阻尼力变化量影响权重趋势，而二阶泰勒展开式是对一阶泰勒展开式的补充，使得其分析结果更为准确，该结论与轨迹灵敏度泰勒展开式分析结论相一致。

4 结束语

本文以磁流变液为研究对象，使用一阶输出灵敏度和二阶输出灵敏度两种灵敏度分析方法，研究了磁流变液的10个参数灵敏度，力求为磁流变液的优化设计及振动控制算法的完善提供基础。

本文以伪静力模型和Bingham流体模型为基础建立了磁流变液阻尼力的数学模型，在此基础上推导出了一阶输出灵敏度和二阶输出灵敏度的函数表达式，对10个参数进行了灵敏度仿真分析。当参数变化量相同时，活塞运动速度、铁芯的横截面积、磁流变液的表观粘度系数、活塞轴直径和活塞的有效长度5个参数使得磁流变液阻尼力变化较小，磁流变液阻尼器的控制电流和活塞阻尼环内径引起阻尼力变化相对较大，而励磁线圈匝数、铁芯的磁导率和外筒和活塞之间的间隙引起阻尼力变化很大，设计磁流变液阻尼器时需要着重考虑。

本研究所得到的理论模型和分析方法可为磁流变液阻尼器阻尼力建模、磁流变液阻尼器的设计及半主动振动控制算法的完善提供参考。