一道例题引发的思考

王玉珍

有位同学在学习苏科版《数学》九年级上册第四章“等可能条件下的概率”的一道例题后，与老师交流了自己的思考，具体内容如下：

一、例题再现

一个不透明的袋子中装有1个白球和2个红球，这些球除颜色外都相同，搅匀后从袋中任意摸出1个球，记录颜色后放回、摇匀，再从中任意摸出1个球.求两次摸到红球的概率.

【解析】从题目中的“不透明”发现这是一个随机事件，把两个红球编号，再“摇匀”，说明摸到每一个球的机会均等，所以这是一个等可能事件.借助树状图或表格列出所有可能的结果，再代入等可能条件下的概率公式即可求出.

把两个红球编号为红球1、红球2，用表格列出所有可能的结果：

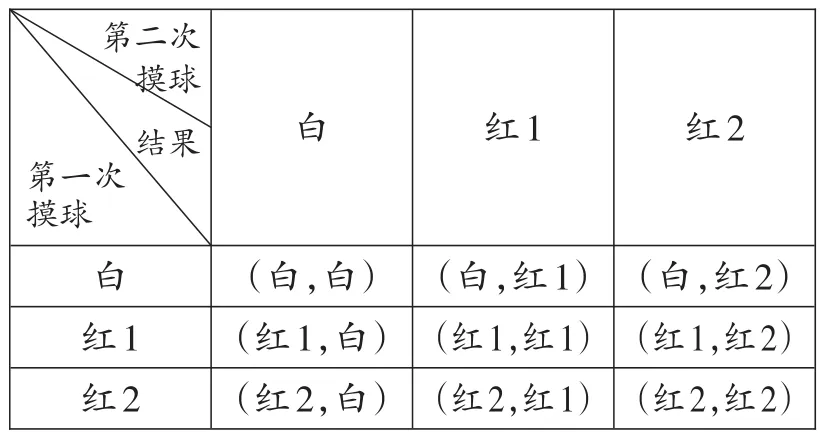
第二次摸球结果白红1红2第一次摸球白红1红2（白，白）（红1，白）（红2，白）（白，红1）（红1，红1）（红2，红1）（白，红2）（红1，红2）（红2，红2）

由表格可知，共有9种可能出现的结果，并且它们是等可能的.将“两次都摸到红球”记为事件B，它的发生有4种可能，所以事件B发生的概率为：P（B）=.即两次都摸到红球的概率是.

【点评】本题属于摸两次球的情况，可以用树状图或表格列出所有可能的结果.

二、拓展

思考1：如果把例题中的“放回”改为“不放回”，应该怎么做呢？

【解析】本题是一个求等可能条件下的概率问题，“不放回”就是摸到一个球以后，下次再摸就不会摸到同一个球.

把两个红球编号为红球1、红球2，用表格列出所有可能结果：

第二次摸球结果白红1红2第一次摸球白（白，红1）红1红2（红1，白）（红2，白）（白，红2）（红1，红2）（红2，红1）

由表格可知，共有6种可能的结果，并且它们是等可能的.将“两次都摸到红球”记为事件B，它的发生有2种可能，所以事件B发生的概率P（B）==.即两次都摸到红球的概率是.

【点评】“不放回”表格内的数据要少一些，不出现的情况用斜线划掉，所以遇到概率问题时我们要看清题目中的关键词.

思考2：如果把例题中两个红球拿掉1个，又按照之前的方法再摸一次，求3次都摸到红球的概率.应该怎么做呢？

【解析】本题是一个求等可能条件下的概率问题.表格只适用于两次摸球的情况，3次就不够用了，所以本题只能用树状图列出所有可能的结果.

用树状图列出所有可能的结果：

由上图可知，共有8种可能的结果，并且它们是等可能的.将“3次都摸到红球”记为事件B，它的发生有1种可能，所以事件B发生的概率：P（B）=.即3次都摸到红球的概率是.

【点评】课本例题出现过横着画的树状图，如果摸3次的话，纵向占用的空间比较大.

思考3：如果把例题中“放回”改为“不放回”，又按照之前的方法再摸一次，求“前两次摸到红球，最后一次摸到白球”的概率.这又应该怎么做呢？

【解析】解题思路与思考2类似.再抓住题目中的关键词“不放回”即可.

把2个红球编号为红球1、红球2，用树状图列出所有可能的结果：

由上图可知，共有6种可能的结果，并且它们是等可能的.将“前两次都摸到红球，最后一次摸到白球”记为事件B，它的发生有2种可能，所以事件B发生的概率：P（B）==.即前两次都摸到红球，最后一次摸到白球的概率是.

【点评】沿用思考2中的画图方法，同学们可将此处的树状图横向绘制，感受一下解题方法的多样性.

三、小结

遇到问题，我们应该仔细、认真读题，抓住题目中的关键词，搞清题目的意思，再“对症下药”.比如两次摸球，既可以用表格，也可以用树状图列出所有可能的结果，用哪一种更好呢？笔者认为，球的总数在4个以内，同学们可根据自己的喜好随便选，但总数等于或超过4个的话，用表格可能更好一些.另外，列表格时题目中出现“不放回”，需把不出现的情况用斜线划掉.再比如3次摸球，表格就满足不了，只能用树状图列出所有可能的结果了，横着画还是竖着画，就根据个人喜好了.