解决“等可能条件下的概率”问题的策略与方法
2018-11-26李进
李 进

解决等可能条件下的概率是中考的重点,也是热点,解题方法多种多样,令不少同学感到变幻莫测,其实解决等可能条件下的概率问题还是有法可依的.下面我们进行归纳分析,以供同学们参考.
一、概念巩固
等可能性:一般地,设一个试验的所有等可能发生的结果有n个,它们都是随机事件,每次试验有且只有一个结果出现,如果每个结果出现的机会均等,那么我们说这n个事件的发生是等可能的,也称这个试验的结果具有等可能性.例如,“摸球试验”“抛硬币试验”“抛掷骰子试验”“抽签试验”等.
等可能事件的概率:一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A的发生有其中的m种结果,那么事件A发生的概率P(A)=.
二、解题常用方法与策略
类型1:列举法求概率.
列举法分为:列表法和画树状图法,这属于中考高频考点.
例1 经典题型:一个不透明的袋子中放了编号为1,2,3的3个球,除编号外其他完全相同.
(1)从中抓取两个球,请问它们的和为奇数的概率为_______.
(2)先从袋中取出一个球,记下数字,放回后搅匀,再摸一个球并记下数字,这两个数字之和是奇数的概率为________.
【解析】考点:等可能事件的概率.(1)分析:由“除编号不同,其余都相同”,确定该事件是等可能事件,问题(1)是一次抓两个球,属于不放回地摸球,用树状图表示所有结果:

所有等可能结果数n=6,和为奇数的结果共有m=4种可能,所以P(两个球和是奇数)=
(2)本题区别于第一问,属于放回式摸球,用树状图表示所有结果:
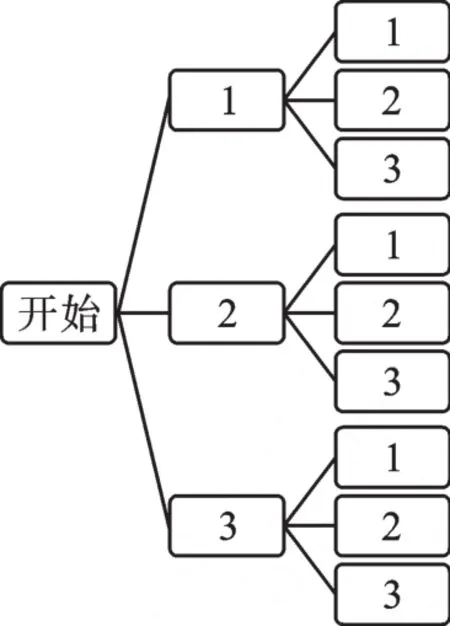
所有等可能的结果数n=9,和为奇数的结果共有m=4种可能,所以P(两个球和是奇数)=.
例2 4张扑克牌的点数分别是2,3,4,8,除点数不同外,其余都相同,将它们洗匀后背面朝上放在桌上.
(1)从中随机抽取一张牌,求这张牌的点数是偶数的概率.
(2)随机抽取一张牌不放回,接着再抽取一张牌,求这两张牌的点数都是偶数的概率.
【解析】考点:等可能事件的概率.
(1)分析:由“除点数不同外,其余都相同”,确定该事件是等可能事件.所有结果为2,3,4,8,其中3种是偶数,即所有等可能结果数n=4,其中符合条件的结果数m=3,所以P(点数是偶数)=.
(2)用树状图表示所有可能的结果:

共有n=12种等可能的结果,其中有m=6种符合条件的结果,所以P(两张牌的点数都是偶数)=
【点评】(1)解决等可能条件下的概率问题,首先要确定该事件结果具有等可能性,然后再解题.(2)解题的关键是,两次摸牌是不放回的.如果是放回地摸,这里的n=16,m=9,那么P(两张牌的点数都是偶数)=.
类型2:用面积求概率.
例3 如图,在一个可以自由转动的转盘中,指针位置固定,3个扇形的面积都相等,且分別标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为_______.
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字.求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).
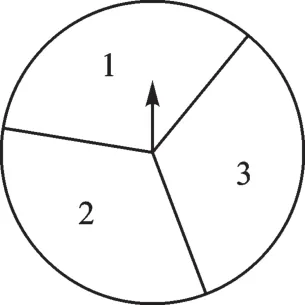
【解析】考点:等可能条件下的概率.(1)由“3个扇形的面积都相等”,可知该试验是等可能性的.所有可能结果有n=3种,符合条件的结果有m=2种,所以P(扇形中的数字是奇数)=.(2)区别于(1),该题解题关键是判别该试验属于放回式摸球试验.用列表法表示所有可能的结果:____________________________

第1次和第2次_____________________________________________________1_________________2_________________3 1 2_________3_________4_________2 3_________4_________5_________3 4____5____6____
