通过合理转化,解决“函数零点问题”
2018-11-23李净
新高考·高三数学 2018年7期
李净


函数的零点问题作为高考填空題的热点和难点,常常作为小题压轴出场,一方面,函数的零点问题涉及的知识点众多,与函数的图象与性质、零点存在定理、导数等知识都有着千丝万缕的联系,综合性很强;另一方面,此类问题的设置常常考查同学们转化化归、数形结合、分类讨论等数学思想方法,需要准确理解题意,选择恰当的方法解题.
那么如何选择恰当的解题方法?可以从分析问题的函数背景人手,探寻题目的隐含条件,通过灵活的条件转化,化归为更简单、更熟悉的问题,指向求解的目标.
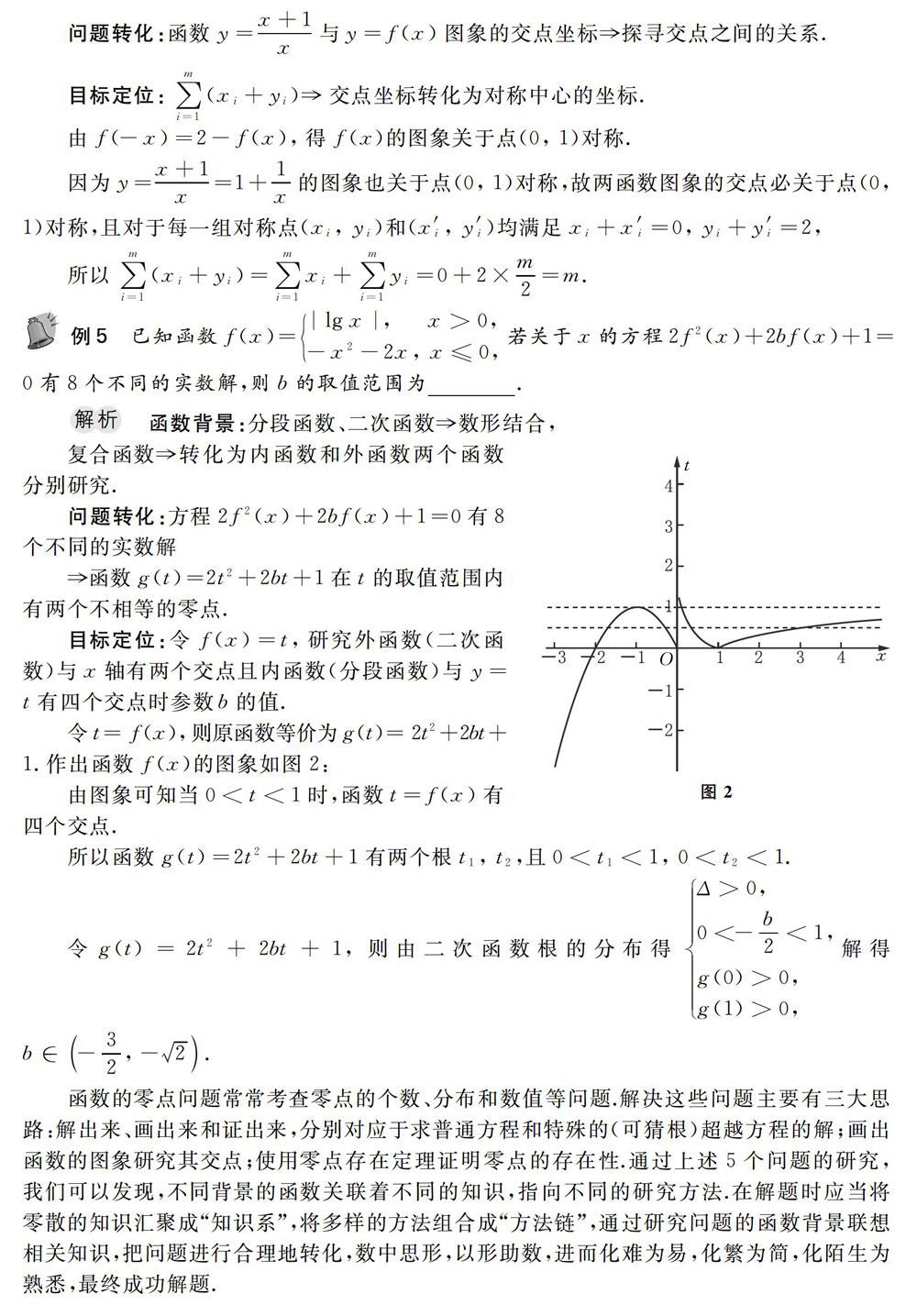
函数的零点问题常常考查零点的个数、分布和数值等问题.解决这些问题主要有三大思路:解出来、画出来和证出来,分别对应于求普通方程和特殊的(可猜根)超越方程的解;画出函数的图象研究其交点;使用零点存在定理证明零点的存在性,通过上述5个问题的研究,我们可以发现,不同背景的函数关联着不同的知识,指向不同的研究方法,在解题时应当将零散的知识汇聚成“知识系”,将多样的方法组合成“方法链”,通过研究问题的函数背景联想相关知识,把问题进行合理地转化,数中思形,以形助数,进而化难为易,化繁为简,化陌生为熟悉,最终成功解题.
