细长钢杆受压稳定分析
2018-11-23
(华南理工大学 广东 广州 510000)
随着我国国民经济的迅猛发展,各种复杂体型的钢结构应运而生,然而,钢结构常存在失稳屈曲问题,人们开始对大跨度钢析架施工过程中所表现出的诸多力学及技术问题愈来愈重视。其中,细长钢杆受压失稳分析是非常具有代表性的问题。[1]
非线性分析,尤其是几何非线性分析在很多情况下是去估算一个结构在失去稳定性前所能承受的最大载荷。线性屈曲分析方法主要通过小位移线性理论假设建立弯曲平衡方程。小位移线性理论假设在结构受载变形过程忽略了结构的构形变化,因此外载施加各个阶段,总是在结构未受载时的构形上产生平衡,当屈由产生时,结构构形突然跳到另一个平衡位置。[2]严格说来,一个受载结构仅在变形后的位置上才处于静平衡状态,从加载一开始就出现了几何非线性的特性。曲线是非线性的,一直达到极限,这种在结构变形所有过程中,在变形后构形上考虑平衡一直达到极限的方法称非线性屈曲或称极限屈曲。
在工程实际中分校屈曲现象实为罕见,它仅出现在完全无结构缺陷,完全沿轴向加压的绝对直杆情况下,分枝屈曲现象虽然罕见,但实际中有不少结构屈曲状态接近分枝屈曲。而分校屈曲的计算工作量又远小于计算极限屈曲的工作量。况且,不少作者得出结论,一些中等非线性的屈曲性态,可以用线性屈曲问题特征矢量的线性组合近似得到。因此线性屈曲理论还是有其实际价值。
但经典的线性屈曲理论存在精度差的缺点,在实际应用中还存在适用范围窄的限制。由于数字计算机与有限元法的迅速发展,计算工作盘已不成为一个严重制约因素,因而近年来研究者的注意力多转向了非线性屈曲的领域。非线性屈曲的基本求解方法是逐步施加外载增量。
一、钢材本构关系
钢材本构关系的模型对失稳屈曲的分析有重大影响。在建立本构关系时一般都是基于现有的连续介质力学本构理论,再结合钢材的力学特性,确定甚至调整本构关系中各种所需的材料参数。通常钢材的本构关系可以分为线性弹性阶段和应变强化阶段。其中非线性阶段的强化理论有众多研究成果,成形中常用硬化模型可分为各向同性硬化和随动硬化。
各向同性硬化认为后继屈服面相对初始屈服面只发生大小的变化而位置不变。但该类模型只能描述单一应变路径下的屈服面相似变化,无法描述应变路径改变时材料的包辛格效应和交叉效应。
与各向同性硬化模型不同的是,随动硬化模型只考虑屈服面的位置移动,不考虑屈服面大小的变化。随动硬化模型避免了各向同性硬化模型无法描述包辛格效应的缺点,很快得到了广泛的应用,如线性随动硬化、多曲面硬化模型、Armstrong-Frederic非线性随动硬化模型。以及在Armstrong-Frederic 模型基础上改进的Chaboche 系列非线性随动硬化模型。因此在Ansys Workbench中有以下5中定义材料非线性硬化方式。
(1)双线性各向同性硬化。(2)多线性各向同性硬化。(3)双线性随动硬化。(4)多线性随动硬化。(5)Chaboche随动硬化。
二、几何非线性
屈曲的含义可简述为:结构处于一种平衡状态,载荷增量为一个微量,其位移增量很大。用方程来表达这种物理现象,则由总体拉格朗日列式法建立的结构刚度方程
[KT]d{δ}=0
(2-1)
根据屈曲含义
[KT]=[K0]+[Kσ]+[KL]
(2-2)
将式(2-2)代入(2-1)得
([K0]+[Kσ]+[KL])d{δ}=0
(2-3)
在线性屈曲情况下,屈曲前结构处于原始位形的线性平衡状态,因此上式中的大位移矩阵[KL]应为零,此时式(3-3)简化为
([K0]+[Kσ])d{δ}=0
(2-4)


(2-5)
代入式(2-4),则有

(2-6)
可以看出式(2-6)是一个广义特征值方程,也是经典弹性稳定理论的最后控制方程。
实际求解时可按以下步骤进行:
(1)按线弹性问题的有限元法形成各单元的刚度矩阵[k0],并用常规方法组装成结构刚度矩阵,即[K0]=∑[k0]。
(2)对结构施加参考载荷{Fr},并求解有限元方程[K0]{δ}={Fr},进而可求得各单元节点应力。

值得指出的是,由式(2-6)所表征的线性屈曲问题,是建立在下述假设的基础上的,即假设线性应变刚度矩阵在屈曲前不产生明显的变化,且初应力矩阵简单地与应力水平成正比。如前所述,这在实际问题中是很罕见的。由式(2-6)所确定的极值载荷只能是近似的。由于线性屈曲理论存在精度差,以及适用范围窄的限制,所以,在一般情况下,应当用切线刚度矩阵[KT]来研究这个问题。当[KT]d{δ}≡0时,发生随遇平衡。显然,这里应该用逐次逼近的方法进行求解。
三、计算模型
分析一个内径为40mm,外径为50mm长为2000mm的细长圆钢管,钢材为Q235钢,杆一端为基础固接,另一端受轴心压力作用。在AnsysWorkbench中建立如图4-2所示的实体模型。非线性分析时,在一秒时间内把轴心压力加到30kN。算例的截面特性为:
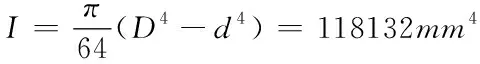

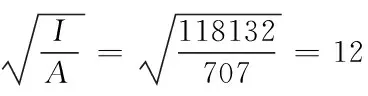
长细比:λ=l0/i=2000/12.93=154.68
长细比大于150,属于细长杆件,进行杆件稳定分析。
分根据析结果,一阶线性屈曲应力为23846N,非线性屈曲分析折算结果为24029N结果较接近。
